Published online by Cambridge University Press: 16 June 2014
We give a separability criterion for the polynomials of the form Using this separability criterion, we prove a sufficient condition using the Brauer–Manin obstruction under which curves of the form 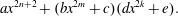 $$\begin{equation*} ax^{2n + 2} + (bx^{2m} + c)(d x^{2k} + e). \end{equation*}$$ have no rational points. As an illustration, using the sufficient condition, we study the arithmetic of hyperelliptic curves of the above form and show that there are infinitely many curves of the above form that are counterexamples to the Hasse principle explained by the Brauer–Manin obstruction.
$$\begin{equation*} ax^{2n + 2} + (bx^{2m} + c)(d x^{2k} + e). \end{equation*}$$ have no rational points. As an illustration, using the sufficient condition, we study the arithmetic of hyperelliptic curves of the above form and show that there are infinitely many curves of the above form that are counterexamples to the Hasse principle explained by the Brauer–Manin obstruction.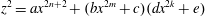 $$\begin{equation*} z^2 = ax^{2n + 2} + (bx^{2m} + c)(d x^{2k} + e) \end{equation*}$$
$$\begin{equation*} z^2 = ax^{2n + 2} + (bx^{2m} + c)(d x^{2k} + e) \end{equation*}$$