Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1966.
Lectures on Functional Equations their and Applications.
Vol. 19,
Issue. ,
p.
383.
Szekeres, G.
1971.
Infinite iteration of integral summation methods.
Journal d'Analyse Mathématique,
Vol. 24,
Issue. 1,
p.
1.
Boshernitzan, Michael
1981.
An extension of hardy’s classL of “orders of infinity”.
Journal d'Analyse Mathématique,
Vol. 39,
Issue. 1,
p.
235.
Boshernitzan, Michael
1986.
Hardy fields and existence of transexponential functions.
Aequationes Mathematicae,
Vol. 30,
Issue. 1,
p.
258.
Waldvogel, Jörg
1988.
Numerical Integration III.
Vol. 85,
Issue. ,
p.
295.
Walker, Peter L.
1988.
A Class of functional equations which have entire solutions.
Bulletin of the Australian Mathematical Society,
Vol. 38,
Issue. 3,
p.
351.
Walker, Peter L.
1990.
The exponential of iteration of 𝑒^{𝑥}-1.
Proceedings of the American Mathematical Society,
Vol. 110,
Issue. 3,
p.
611.
Boshernitzan, Michael D.
1994.
Uniform distribution and Hardy fields.
Journal d'Analyse Mathématique,
Vol. 62,
Issue. 1,
p.
225.
Miltersen, Peter Bro
Vinodchandran, N. V.
and
Watanabe, Osamu
1999.
Computing and Combinatorics.
Vol. 1627,
Issue. ,
p.
210.
2005.
Gesammelte Abhandlungen / Collected Papers.
Trappmann, Henryk
and
Kouznetsov, Dimitrii
2011.
Uniqueness of holomorphic Abel functions at a complex fixed point pair.
Aequationes mathematicae,
Vol. 81,
Issue. 1-2,
p.
65.
Bonet, José
and
Domański, Paweł
2015.
Abel’s Functional Equation and Eigenvalues of Composition Operators on Spaces of Real Analytic Functions.
Integral Equations and Operator Theory,
Vol. 81,
Issue. 4,
p.
455.
KOŁODZIEJCZYK, LESZEK ALEKSANDER
2016.
END-EXTENSIONS OF MODELS OF WEAK ARITHMETIC FROM COMPLEXITY-THEORETIC CONTAINMENTS.
The Journal of Symbolic Logic,
Vol. 81,
Issue. 3,
p.
901.
Izumi, Hideaki
2016.
The prompter method: A treatment for hard-to-solve iterative functional equations.
Journal of Symbolic Computation,
Vol. 75,
Issue. ,
p.
193.
Dijoux, Yann
2020.
Construction of the tetration distribution based on the continuous iteration of the exponential‐minus‐one function.
Applied Stochastic Models in Business and Industry,
Vol. 36,
Issue. 5,
p.
891.
Dijoux, Yann
2023.
A new class of distributions on the whole real line based on the continuous iteration approach.
Communications in Statistics - Theory and Methods,
Vol. 52,
Issue. 14,
p.
4934.
 have frequently been discussed in literature. G. H. Hardy has shown (in [3], and in greater detail in [4]) that the asymptotic behaviour of the solutions of (1) cannot be expressed in terms of the logarithmico-exponential scale, although they are comparable with each member of the scale.1 Hence solutions of (1) provide a remarkably simple instance of functions whose manner of growth does not fit into the scale of L-functions but requires non-elementary orders of infinity for an accurate representation. This raises quite naturally the question whether there exists a most regularly growing solution of equation (1) which might serve as a prototype for this kind of growth. In a slightly more general context we may ask whether there exists a ‘best’ family of fractional iterates fσ(x), satisfying
have frequently been discussed in literature. G. H. Hardy has shown (in [3], and in greater detail in [4]) that the asymptotic behaviour of the solutions of (1) cannot be expressed in terms of the logarithmico-exponential scale, although they are comparable with each member of the scale.1 Hence solutions of (1) provide a remarkably simple instance of functions whose manner of growth does not fit into the scale of L-functions but requires non-elementary orders of infinity for an accurate representation. This raises quite naturally the question whether there exists a most regularly growing solution of equation (1) which might serve as a prototype for this kind of growth. In a slightly more general context we may ask whether there exists a ‘best’ family of fractional iterates fσ(x), satisfying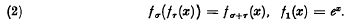 .
.