Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
McBride, Adam C.
1975.
A Theory of Fractional Integration for Generalized Functions.
SIAM Journal on Mathematical Analysis,
Vol. 6,
Issue. 3,
p.
583.
McBride, Adam C.
1975.
Solution of hypergeometric integral equations involving generalised functions.
Proceedings of the Edinburgh Mathematical Society,
Vol. 19,
Issue. 3,
p.
265.
Love, Eric Russell
1975.
Fractional Calculus and Its Applications.
Vol. 457,
Issue. ,
p.
272.
Erdélyi, Arthur
1975.
Fractional Calculus and Its Applications.
Vol. 457,
Issue. ,
p.
151.
Braaksma, B. L. J.
and
Schuitman, A.
1976.
Some Classes of Watson Transforms and Related Integral Equations for Generalized Functions.
SIAM Journal on Mathematical Analysis,
Vol. 7,
Issue. 6,
p.
771.
Orton, Marion
1980.
The Generalized Abel Equations for Schwartz Distributions.
SIAM Journal on Mathematical Analysis,
Vol. 11,
Issue. 3,
p.
596.
Mcbride, Adam C.
1983.
A note on the index laws of fractional calculus.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 34,
Issue. 3,
p.
356.
Bonilla, B.
Trujillo, J.J.
and
Rivero, M.
1999.
Fractional Order Continuity and Some Properties about Integrability and Differentiability of Real Functions.
Journal of Mathematical Analysis and Applications,
Vol. 231,
Issue. 1,
p.
205.
Li, Chenkuan
and
Li, Changpin
2014.
On defining the distributions δk and (δ′)k by fractional derivatives.
Applied Mathematics and Computation,
Vol. 246,
Issue. ,
p.
502.
Li, Chenkuan
and
Li, Changpin
2017.
Remarks on fractional derivatives of distributions*.
Tbilisi Mathematical Journal,
Vol. 10,
Issue. 1,
Kukushkin, Maksim V.
2022.
Evolution Equations in Hilbert Spaces via the Lacunae Method.
Fractal and Fractional,
Vol. 6,
Issue. 5,
p.
229.
Kukushkin, M. V.
2023.
Kipriyanov’s Fractional Calculus Prehistory and Legacy.
Lobachevskii Journal of Mathematics,
Vol. 44,
Issue. 8,
p.
3411.
Hilfer, R.
and
Kleiner, T.
2024.
Fractional calculus for distributions.
Fractional Calculus and Applied Analysis,
Vol. 27,
Issue. 5,
p.
2063.
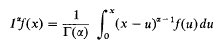 if Reα > 0, can be extended to generalised functions in the framework of the theory of convolution of distributions. The resulting theory [2, Chap. I §5.5] is very satisfactory for many purposes but there are circumstances in which it is not suitable. Such circumstances arise in particular if it is necessary to multiply, before or after integratrion, by non-integral powers of the variable. Pointwise multiplication by fractional powers of the independent variable does not make sense in the theory of distributions.
if Reα > 0, can be extended to generalised functions in the framework of the theory of convolution of distributions. The resulting theory [2, Chap. I §5.5] is very satisfactory for many purposes but there are circumstances in which it is not suitable. Such circumstances arise in particular if it is necessary to multiply, before or after integratrion, by non-integral powers of the variable. Pointwise multiplication by fractional powers of the independent variable does not make sense in the theory of distributions.

