Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Farshadfar, Hamidreza
Shamsi Armandi, Hamzeh
Gharibshahi, Reza
and
Jafari, Arezou
2023.
Simultaneous electromagnetic radiation and nanofluid injection and their interactions in EOR operations: A comprehensive review.
Journal of Magnetism and Magnetic Materials,
Vol. 580,
Issue. ,
p.
170863.



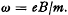 .
.