The well-known Banach Contraction Principle asserts that any self-map F of a complete metric space M with the property that, for some number k < 1,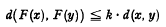 for all x, y,∈M, possesses a unique fixed point in M. some extensions and analogues have recently been given by Edelstein [1]. For the reader's convenlience we state here the result of Edelstein which we shall employ. It asserts that if F is a self-map of a metric space M having the property that 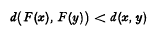for any two distinct points x and y of M, and if x0 is a point of M such that the sequence of iterates xn = Fn (x0) contains a subsequence which converges in M, then the limit of this subsequence is the unique fixed point of F.