Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T20:33:04.695Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITELY DOMINATED COVERING SPACES OF 3- AND 4-MANIFOLDS

Part of: Connections with homological algebra and category theory Topological manifolds

Published online by Cambridge University Press:  01 February 2008

JONATHAN A. HILLMAN
JONATHAN A. HILLMAN*
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If P is a closed 3-manifold the covering space associated to a finitely presentable subgroup ν of infinite index in π1(P) is finitely dominated if and only if P is aspherical or 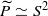. There is a corresponding result in dimension 4, under further hypotheses on π and ν. In particular, if M is a closed 4-manifold, ν is an ascendant, FP3, finitely-ended subgroup of infinite index in π1(M), π is virtually torsion free and the associated covering space is finitely dominated then either M is aspherical or 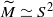or S3. In the aspherical case such an ascendant subgroup is usually Z, a surface group or a PD3-group.

Keywords

finitely dominated4-manifoldPoincaré duality groupsubnormal subgroup

MSC classification

Secondary: 57N13: Topology of $E^4$, $4$-manifolds 20J05: Homological methods in group theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 1 , February 2008 , pp. 99 - 108
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Bieri, R., Homological dimensions of discrete groups, Queen Mary College Mathematics Notes (Queen Mary College, London, 1976).Google Scholar
[2]Bowditch, B. H., ‘Planar groups and the Seifert conjecture’, J. Reine Angew. Math. 576 (2004), 11–62.Google Scholar
[3]Burns, R. G., ‘A note on free groups’, Proc. Amer. Math. Soc. 23 (1969), 14–17.CrossRefGoogle Scholar
[4]Crisp, J., ‘The decomposition of 3-dimensional Poincaré duality complexes’, Comment. Math. Helv. 75 (2000), 232–246.CrossRefGoogle Scholar
[5]Farrell, F. T., ‘The second cohomology group of G with coefficients Z/2Z[G]’, Topology 13 (1974), 313–326.CrossRefGoogle Scholar
[6]Farrell, F. T., ‘Poincaré duality and groups of type FP’, Comment. Math. Helv. 50 (1975), 187–195.CrossRefGoogle Scholar
[7]Geoghegan, R. and Mihalik, M. L., ‘A note on the vanishing of H n(G;Z[G])’, J. Pure Appl. Algebra 39 (1986), 301–304.CrossRefGoogle Scholar
[8]Gildenhuys, D. and Strebel, R., ‘On the cohomological dimension of soluble groups’, Canad. Math. Bull. 24 (1981), 385–392.CrossRefGoogle Scholar
[9]Hillman, J. A., Four-manifolds, geometries and knots, Geometry and Topology Monographs, 5 (Geometry and Topology Publications, University of Warwick, Coventry, 2002).Google Scholar
[10]Hillman, J. A., ‘Centralizers and normalizers in PD 3-groups and open PD 3-groups’, J. Pure Appl. Algebra 204 (2006), 244–257.CrossRefGoogle Scholar
[11]Hillman, J. A. and Kochloukova, D. S., ‘Finiteness conditions and PD r-covers of PD n-complexes’, Math. Z. 256 (2007), 45–56.CrossRefGoogle Scholar
[12]Mess, G., ‘Examples of Poincaré duality groups’, Proc. Amer. Math. Soc. 110 (1990), 1144–1145.Google Scholar
[13]Mihalik, M. L., ‘Ends of double extension groups’, Topology 25 (1986), 45–53.CrossRefGoogle Scholar
[14]Milnor, J. W., ‘Infinite cyclic coverings’, Conference on the Topology of Manifolds (ed. J. G. Hocking) (Prindle, Weber and Schmidt, Boston, London, Sydney, 1968), pp. 115–133.Google Scholar
[15]Robinson, D. J. S., ‘On the cohomology of soluble groups of finite rank’, J. Pure Appl. Algebra 6 (1975), 155–164.CrossRefGoogle Scholar
[16]Strebel, R., ‘A remark on subgroups of infinite index in Poincaré duality groups’, Comment. Math. Helv. 52 (1977), 317–324.CrossRefGoogle Scholar