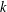Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T14:25:22.939Z Has data issue: false hasContentIssue false
  • English
  • Français

FACTORS OF CARMICHAEL NUMBERS AND A WEAK $k$-TUPLES CONJECTURE

Part of: Elementary number theory

Published online by Cambridge University Press:  17 November 2015

THOMAS WRIGHT
THOMAS WRIGHT*
Affiliation:
Department of Mathematics, Wofford College, 429 N. Church St., Spartanburg, SC 29302, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In light of the recent work by Maynard and Tao on the Dickson 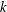$k$-tuples conjecture, we show that with a small improvement in the known bounds for this conjecture, we would be able to prove that for some fixed 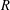$R$, there are infinitely many Carmichael numbers with exactly 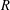$R$ factors for some fixed 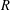$R$. In fact, we show that there are infinitely many such 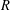$R$.

Keywords

Carmichael numbersDickson’s conjectureprime k-tuplespseudoprimes

MSC classification

Primary: 11A51: Factorization; primality
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 3 , June 2016 , pp. 421 - 429
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Alford, W. R., Grantham, J., Hayman, S. and Shallue, A., ‘Constructing Carmichael numbers through improved subset-product algorithms’, Math. Comp. 83 (2014), 899–915.Google Scholar
Alford, W. R., Granville, A. and Pomerance, C., ‘There are infinitely many Carmichael numbers’, Ann. of Math. (2) 139(3) (1994), 703–722.CrossRefGoogle Scholar
Carmichael, R. D., ‘Note on a new number theory function’, Bull. Amer. Math. Soc. 16 (1910), 232–238.Google Scholar
Chernick, J., ‘On Fermat’s simple theorem’, Bull. Amer. Math. Soc. 45 (1939), 269–274.CrossRefGoogle Scholar
Van Emde Boas, P. and Kruyswijk, D., ‘A combinatorial problem on finite Abelian groups III’, Report ZW 1969-008, Stichting Mathematisch Centrum, Amsterdam, 1969.Google Scholar
Granville, A. and Pomerance, C., ‘Two contradictory conjectures concerning Carmichael numbers’, Math. Comp. 71 (2002), 883–908.CrossRefGoogle Scholar
Korselt, A., ‘Problème chinois’, L’intermédinaire des Mathématiciens 6 (1899), 142–143.Google Scholar
Matomäki, K., ‘On Carmichael numbers in arithmetic progressions’, J. Aust. Math. Soc. 2 (2013), 1–8.Google Scholar
Maynard, J., ‘Small gaps between primes’, Ann. of Math. (2) 181 (2015), 383–413.Google Scholar
Meshulam, R., ‘An uncertainty inequality and zero subsums’, Discrete Math. 84(2) (1990), 197–200.Google Scholar
Wright, T., ‘Infinitely many Carmichael numbers in arithmetic progressions’, Bull. Lond. Math. Soc. 45 (2013), 943–952.CrossRefGoogle Scholar