Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T04:52:59.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Extrema of random algebraic polynomials with non-identically distributed normal coefficients

Part of: Stochastic processes Stochastic analysis

Published online by Cambridge University Press:  09 April 2009

K. Farahmand  and
A. Grigorash
A. Grigorash
Affiliation:
Department of Mathematics, University of Ulster at Jordanstown, Co. Antrim, BT37 0QB, United Kingdom e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An asymptotic estimate is derived for the expected number of extrema of a polynomial 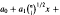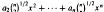whose independent normal coefficients possess non-equal non-zero mean values. A result is presented that generalizes in terms of normal processes the analytical device used for construction of similar asymptotic estimates for random polynomials with normal coefficients.

Keywords

number of real zerosreal rootsnumber of extremarandom algebraic polynomialsnormal stochastic processesasymptotic estimate.

MSC classification

Secondary: 60H99: None of the above, but in this section 60G15: Gaussian processes
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 70 , Issue 2 , April 2001 , pp. 225 - 234
Copyright
Copyright © Australian Mathematical Society 2001

References

[1]Belayev, Yu. K., ‘Continuity and Hölder's conditions for sample functions of stationary Gaussian processes’, Proc. 4th Berkeley Sympos. on Math. Statist. and Prob. II (Univ. California Press, Berkeley, 1961), 23–33.Google Scholar
[2]Bharucha-Reid, A. T. and Sambandham, M., Random polynomials (Academic Press, New York, 1986).Google Scholar
[3]Cramér, H. and Leadbetter, M. R., Stationary and related stochastic processes (Wiley, New York, 1967).Google Scholar
[4]Das, M., ‘The average number of maxima of a random algebraic curve’, Proc. Cambridge Philos. Soc. 65 (1969), 741–753.Google Scholar
[5]Edelman, A. and Kostlan, E., ‘How many zeros of a random polynomial are real?’, Bull. Amer. Math. Soc. 32 (1995), 1–37.CrossRefGoogle Scholar
[6]Farahmand, K.Topics in random polynomials (Addison Wesley Longman, London, 1998).Google Scholar
[7]Farahmand, K. and Grigorash, A., ‘Level crossings of random algebraic polynomials with non-identically distributed normal coefficients’, Int. J. Appl. Math. 2 (2000), 213–221.Google Scholar
[8]Farahmand, K. and Hannigan, P., ‘The expected number of local maxima of a random algebraic polynomial’, J. Theoret. Probab. 10 (1997), 991–1002.CrossRefGoogle Scholar
[9]Leadbetter, M. R., ‘On crossings of levels and curves by a wide class of stochastic processes’, Ann. Math. Statist. 37 (1966), 260–267.CrossRefGoogle Scholar
[10]Marcus, M. B., ‘Level crossings of a stochastic process with absolutely continuous sample paths’, Ann. Probab. 5 (1977), 52–71.CrossRefGoogle Scholar
[11]Michna, Z. and Rychlik, I., ‘The expected number of level crossings for certain symmetric α-stable processes’, Comm. Statist. Stochastic Models 11 (1995), 1–19.Google Scholar
[12]Sambandham, M., ‘On random trigonometric polynomial’, Indian J. Pure Appl. Math. 7 (1976), 841–849.Google Scholar
[13]Wilkins, J. E., ‘An asymptotic expansion for the expected number of real zeros of a random polynomial’, Proc. Amer. Math. Soc. 103 (1988), 1249–1258.Google Scholar