Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T18:30:55.006Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE OF A WEAK SOLUTION FOR A CLASS OF FRACTIONAL LAPLACIAN EQUATIONS

Part of: Elliptic equations and systems Nonlinear operators and their properties

Published online by Cambridge University Press:  09 September 2016

V. RAGHAVENDRA  and
RASMITA KAR
V. RAGHAVENDRA
Affiliation:
Department of Mathematics, LNMIIT, Jaipur-302031, India email [email protected]
RASMITA KAR*
Affiliation:
Department of Mathematics, NIT Rourkela, Rourkela-769008, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the existence of a weak solution of a nonlocal problem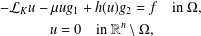

$$\begin{eqnarray}\displaystyle & \displaystyle -{\mathcal{L}}_{K}u-\unicode[STIX]{x1D707}ug_{1}+h(u)g_{2}=f\quad \text{in }\unicode[STIX]{x1D6FA}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle u=0\quad \text{in }\mathbb{R}^{n}\setminus \unicode[STIX]{x1D6FA}, & \displaystyle \nonumber\end{eqnarray}$$
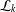where ${\mathcal{L}}_{k}$ is a general nonlocal integrodifferential operator of fractional type, 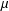$\unicode[STIX]{x1D707}$ is a real parameter and 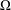$\unicode[STIX]{x1D6FA}$ is an open bounded subset of 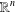$\mathbb{R}^{n}$ (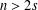$n>2s$, where 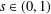$s\in (0,1)$ is fixed) with Lipschitz boundary 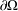$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$. Here 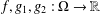$f,g_{1},g_{2}:\unicode[STIX]{x1D6FA}\rightarrow \mathbb{R}$ and 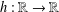$h:\mathbb{R}\rightarrow \mathbb{R}$ are functions satisfying suitable hypotheses.

Keywords

demicontinuous operatorsnonlocal operator

MSC classification

Primary: 35J60: Nonlinear elliptic equations
Secondary: 47H99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 3 , June 2017 , pp. 392 - 404
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Cabré, X. and Tan, J., ‘Positive solutions of nonlinear problems involving the square root of the Laplacian’, Adv. Math. 224 (2010), 2052–2093.Google Scholar
Capella, A., ‘Solutions of a pure critical exponent problem involving the half-Laplacian in annular-shaped domains’, Commun. Pure Appl. Anal. 10 (2011), 1645–1662.CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E., ‘Hitchhiker’s guide to the fractional Sobolev spaces’, Bull. Sci. Math. 136 (2012), 521–573.CrossRefGoogle Scholar
Fiscella, A., ‘Saddle point solutions for non-local elliptic operators’, Preprint, 2012.Google Scholar
Fiscella, A., Servadei, R. and Valdinoci, E., ‘Asymptotically linear problems driven by fractional Laplacian operators’, Math. Methods Appl. Sci. 38(16) (2015), 3551–3563.Google Scholar
Fiscella, A., Servadei, R. and Valdinoci, E., ‘A resonance problem for non-local elliptic operators’, Z. Anal. Anwend. 32 (2013), 411–431.Google Scholar
Hess, P., ‘On the Fredholm alternative for nonlinear functional equations in Banach spaces’, Proc. Amer. Math. Soc. 33 (1972), 55–61.CrossRefGoogle Scholar
Krasnolsel’skii, M. A., Topological Methods in the Theory of Nonlinear Integral Equations (GITTL, Moscow, 1956).Google Scholar
Kufner, A., John, O. and Fučik, S., Functions Spaces (Noordhoff, Leyden, 1977).Google Scholar
Molica Bisci, G., ‘Fractional equations with bounded primitive’, Appl. Math. Lett. 27 (2014), 53–58.CrossRefGoogle Scholar
Molica Bisci, G. and Servadei, R., ‘A bifurcation result for non-local fractional equations’, Anal. Appl. (Singap.) 13(4) (2015), 371–394.Google Scholar
Servadei, R., ‘The Yamabe equation in a non-local setting’, Adv. Nonlinear Anal. 2 (2013), 235–270.Google Scholar
Servadei, R., ‘A critical fractional Laplace equation in the resonant case’, Topol. Methods Nonlinear Anal. 43(1) (2014), 251–267.Google Scholar
Servadei, R. and Valdinoci, E., ‘Fractional Laplacian equations with critical Sobolev exponent’, Rev. Mat. Complut. 28(3) (2015), 655–676.Google Scholar
Servadei, R. and Valdinoci, E., ‘Mountain pass solutions for non-local elliptic operators’, J. Math. Anal. Appl. 389 (2012), 887–898.Google Scholar
Servadei, R. and Valdinoci, E., ‘Lewy–Stampacchia type estimates for variational inequalities driven by (non)local operators’, Rev. Mat. Iberoam. 29(3) (2013), 1091–1126.Google Scholar
Servadei, R. and Valdinoci, E., ‘Variational methods for non-local operators of elliptic type’, Discrete Contin. Dyn. Syst. 33 (2013), 2105–2137.Google Scholar
Servadei, R. and Valdinoci, E., ‘The Brezis–Nirenberg result for the fractional Laplacian’, Trans. Amer. Math. Soc. 367(1) (2015), 67–102.Google Scholar
Tan, J., ‘The Brezis–Nirenberg type problem involving the square root of the Laplacian’, Calc. Var. Partial Differential Equations 36 (2011), 21–41.Google Scholar
Zeidler, E., Nonlinear Functional Analysis and its Applications, Part II/A (Springer, New York, 1990).Google Scholar
Zeidler, E., Nonlinear Functional Analysis and its Applications, Part II/B (Springer, New York, 1990).Google Scholar