Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T11:17:23.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodicity and stability of orbits of unbounded semigroup representations

Part of: Abstract harmonic analysis General theory of linear operators Set functions, measures and integrals with values in abstract spaces Commutative Banach algebras and commutative topological algebras Functional-differential and differential-difference equations

Published online by Cambridge University Press:  09 April 2009

Bolis Basit  and
A. J. Pryde
Bolis Basit
Affiliation:
School of Mathematical Sciences, P.O. Box 28M, Monash University, VIC 3800, Australia e-mail: [email protected]@sci.monash.edu.au
A. J. Pryde
Affiliation:
School of Mathematical Sciences, P.O. Box 28M, Monash University, VIC 3800, Australia e-mail: [email protected]@sci.monash.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop a theory of ergodicity for unbounded functions ø: J → X, where J is a subsemigroup of a locally compact abelian group G and X is a Banach space. It is assumed that ø is continuous and dominated by a weight w defined on G. In particular, we establish total ergodicity for the orbits of an (unbounded) strongly continuous representation T: G → L(X) whose dual representation has no unitary point spectrum. Under additional conditions stability of the orbits follows. To study spectra of functions, we use Beurling algebras L1w(G) and obtain new characterizations of their maximal primary ideals, when w is non-quasianalytic, and of their minimal primary ideals, when w has polynomial growth. It follows that, relative to certain translation invariant function classes 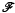, the reduced Beurling spectrum of ø is empty if and only if ø ∈ 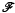. For the zero class, this is Wiener's tauberian theorem.

Keywords

weighted ergodicityorbits of unbounded semigroup representationnon-quasianalytic weightsstabilityBeurling spectrum

MSC classification

Secondary: 46J20: Ideals, maximal ideals, boundaries 43A60: Almost periodic functions on groups and semigroups and their generalizations (recurrent functions, distal functions, etc.); almost automorphic functions 47A35: Ergodic theory 34K25: Asymptotic theory 28B05: Vector-valued set functions, measures and integrals
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 77 , Issue 2 , October 2004 , pp. 209 - 232
Copyright
Copyright © Australian Mathematical Society 2004

References

[1]Arendt, W. and Batty, C. J. K., ‘Tauberian theorems and stability of one-parameter semigroups’, Trans. Amer. Math. Soc. 306 (1988), 837–852.CrossRefGoogle Scholar
[2]Arendt, W. and Batty, C. J. K., ‘Almost periodic solutions of first and second order Cauchy problems’, J. Differential Equations 137 (1997), 363–383.CrossRefGoogle Scholar
[3]Arendt, W. and Batty, C. J. K., ‘Asymptotically almost periodic solutions of of the inhomogeneous Cauchy problems on the half line’, Bull. London Math. Soc. 31 (1999), 291–304.CrossRefGoogle Scholar
[4]Arendt, W. and Prüss, J., ‘Vector-valued Tauberian theorems and asymptotic behavior of linear Voltera equations’, SIAM J. Math. Anal. 23 (1992), 412–418.CrossRefGoogle Scholar
[5]Basit, B., ‘Some problems concerning different types of vector-valued almost periodic functions’, Dissertationes Math. 338 (1995).Google Scholar
[6]Basit, B., ‘Harmonic analysis and asymptotic behavior of solutions to the abstract Cauchy problem’, Semigroup Forum 54 (1997), 58–74.CrossRefGoogle Scholar
[7]Basit, B. and Pryde, A. J., ‘Ergodicity and differences of functions on semigroups’, J. Austral. Math. Soc. Ser. A 64 (1998), 253–265.CrossRefGoogle Scholar
[8]Basit, B. and Pryde, A. J., ‘Polynomials and functions with finite spectra on locally compact abelian groups’, Bull. Austral. Math. Soc. 51 (1995), 33–42.CrossRefGoogle Scholar
[9]Batty, C. J. K., Neerven, J. V. and Räbiger, F., ‘Tauberian theorems and stability of solutions of the Cauchy problem’, Trans. Amer. Math. Soc. 350 (1998), 2087–2103.CrossRefGoogle Scholar
[10]Batty, C. J. K. and Phóng, V. Q., ‘Stability of strongly continuous representations of abelian groups’, Math. Z. 209 (1992), 75–88.CrossRefGoogle Scholar
[11]Batty, C. J. K. and Yeates, S. B., ‘Weighted and local stability of semigroups of operators’, Math. Proc. Cambridge Philos. Soc. 129 (2000), 85–98.CrossRefGoogle Scholar
[12]Basit, B. and Günzler, H., ‘Generalized vector valued almost periodic and ergodic distributions’, Analysis Paper 113, Monash University, 2002.Google Scholar
[13]Basit, B. and Günzler, H., ‘Asymptotic behavior of solutions of neutral equations’, J. Differential Equations 149 (1998), 115–142.CrossRefGoogle Scholar
[14]Domar, Y., ‘Harmonic analysis based on certain commutative Banach algebras’, Acta Math. 96 (1956), 1–66.CrossRefGoogle Scholar
[15]Doss, R., ‘On the almost periodic solutions of a class of integro-differential-difference equations’, Ann. of Math. (2) 81 (1965), 117–123.CrossRefGoogle Scholar
[16]Dunford, N. and Schwartz, J. T., Linear operators, part II: Spectral theory (Interscience, New York, 1963).Google Scholar
[17]Gurarii, V. P., ‘Harmonic analysis in spaces with weight’, Tr. Mosk. Mat. Obs. 35 (1976),Google Scholar
English translation: Trans. Moscow Math. Soc. 1 (1979), 21–75.Google Scholar
[18]Hewitt, E. and Ross, K. A., Abstract harmonic analysis, volume I (Springer, Heidelberg, 1963).Google Scholar
[19]Hewitt, E. and Ross, K. A., Abstract harmonic analysis, volume II (Springer, New York, 1970).Google Scholar
[20]Iseki, K., ‘Vector valued functions on semigroups I, II, III’, Proc. Japan Acad. 31 (1955), 16–19, 152–155, 699–701.Google Scholar
[21]Jacobs, K., ‘Ergodentheorie und Fastperiodische Funktionen auf Halbgruppen’, Math. Z. 64 (1956), 298–338.CrossRefGoogle Scholar
[22]Levitan, B. M. and Zhikov, V. V., Almost periodic functions and differential equations (Cambridge Univ. Press, Cambridge, 1982).Google Scholar
[23]Loomis, L. H., ‘Spectral characterization of almost periodic functions’, Ann. of Math. (2) 72 (1960), 362–368.CrossRefGoogle Scholar
[24]Yu., I. Lyubich, Matsaev, V. I. and Fel'dman, G. M., ‘On representations with a separable spectrum’, Funktsional. Anal. i Prilozhen. 7 (1973),Google Scholar
English translation: Funct. Anal. Appl. 7 (1973), 129–136.CrossRefGoogle Scholar
[25]Maak, W., ‘Abstrakte fastperiodische Funktionen’, Abh. Math. Sem. Univ. Hamburg 6 (1936), 365–380.Google Scholar
[26]Maak, W., ‘Integralmittelwerte von Funktionen auf Gruppen und Halb-gruppen’, J. Reine Angew. Math. 190 (1952), 40–48.Google Scholar
[27]Nillsen, R., Difference spaces and invariant linear forms, Lecture Notes in Math. 1586 (Springer, Berlin, 1994).CrossRefGoogle Scholar
[28]Phóng, V. Q., ‘Semigroups with nonquasianalytic growth’, Studia Mathematica 104 (1993), 229–241.CrossRefGoogle Scholar
[29]Pitt, H. R., ‘General Tauberian theorems’, Proc. London Math. Soc. 44 (1938), 243–288.CrossRefGoogle Scholar
[30]Prüss, J., Evolutionary integral equations and applications (Birkhäuser, Boston, 1993).CrossRefGoogle Scholar
[31]Reiter, H., Classical harmonic analysis and locally compact groups (Clarendon Press, Oxford, 1968).Google Scholar
[32]Rudin, W., Harmonic analysis on groups (Interscience, New York, 1962).Google Scholar
[33]Ruess, W. M. and Phóng, V. Q., ‘Asymptotically almost periodic solutions of evolution equations in Banach spaces’, J. Differential Equations 122 (1995), 282–301.CrossRefGoogle Scholar
[34]Yosida, K., Functional analysis (Springer, Berlin, 1976).Google Scholar
[35]Zarrabi, M., ‘Contractions à spectre dénombrable et propriétés d'unicité des fermés dénombrables du circle’, Ann. Inst. Fourier (Grenoble) 43 (1993), 251–263.CrossRefGoogle Scholar