Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tan, Zhongquan
and
Peng, Zuoxiang
2009.
Almost sure convergence for non-stationary random sequences.
Statistics & Probability Letters,
Vol. 79,
Issue. 7,
p.
857.
Tong, Bin
and
Peng, Zuo Xiang
2011.
On almost sure max-limit theorems of complete and incomplete samples from stationary sequences.
Acta Mathematica Sinica, English Series,
Vol. 27,
Issue. 7,
p.
1323.


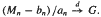 . In this paper, we shall show that {(
. In this paper, we shall show that {(