Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bowshell, R. A.
and
Schultz, P.
1977.
Unital rings whose additive endomorphisms commute.
Mathematische Annalen,
Vol. 228,
Issue. 3,
p.
197.
Reid, J. D.
1977.
Abelian Group Theory.
Vol. 616,
Issue. ,
p.
219.
Arnold, D
Pierce, R.S
Reid, J.D
Vinsonhaler, C
and
Wickless, W
1981.
Torsion-free abelian groups of finite rank projective as modules over their endomorphism rings.
Journal of Algebra,
Vol. 71,
Issue. 1,
p.
1.
Reid, J. D.
1981.
Abelian Group Theory.
Vol. 874,
Issue. ,
p.
41.
Mishina, A. P.
1982.
Abelian groups.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 5,
p.
629.
Pierce, R. S.
and
Vinsonhaler, C. I.
1983.
Abelian Group Theory.
Vol. 1006,
Issue. ,
p.
49.
Hausen, Jutta
1983.
Abelian Group Theory.
Vol. 1006,
Issue. ,
p.
204.
Reid, J. D.
1983.
Abelian Group Theory.
Vol. 1006,
Issue. ,
p.
190.
Hausen, Jutta
1984.
Abelian Groups and Modules.
Vol. 287,
Issue. ,
p.
181.
Vinsonhaler, C.
1984.
Abelian Groups and Modules.
Vol. 287,
Issue. ,
p.
163.
Hausen, Jutta
1985.
Finite rank torsion-free abelian groups uniserial over their endomorphism rings.
Proceedings of the American Mathematical Society,
Vol. 93,
Issue. 2,
p.
227.
Markov, V. T.
Mikhalev, A. V.
Skornyakov, L. A.
and
Tuganbaev, A. A.
1985.
Endomorphism rings of modules and lattices of submodules.
Journal of Soviet Mathematics,
Vol. 31,
Issue. 3,
p.
3005.
Vinsonhaler, C.
and
Wickless, W.
1985.
Locally irreducible rings.
Bulletin of the Australian Mathematical Society,
Vol. 32,
Issue. 1,
p.
129.
Faticoni, Theodore G.
1987.
Each countable reduced torsion-free commutative ring is a pure subring of an e-ring.
Communications in Algebra,
Vol. 15,
Issue. 12,
p.
2545.
Hausen, Jutta
1987.
E-transitive torsion-free abelian groups.
Journal of Algebra,
Vol. 107,
Issue. 1,
p.
17.
Dugas, Manfred
Mader, Adolf
and
Vinsonhaler, Charles
1987.
Large E-rings exist.
Journal of Algebra,
Vol. 108,
Issue. 1,
p.
88.
Albrecht, Ulrich
1988.
Faithful abelian groups of infinite rank.
Proceedings of the American Mathematical Society,
Vol. 103,
Issue. 1,
p.
21.
Mader, A
and
Vinsonhaler, C
1988.
Torsion-free E-modules.
Journal of Algebra,
Vol. 115,
Issue. 2,
p.
401.
Dugas, Manfred
and
G�bel, R�diger
1990.
Torsion-free nilpotent groups andE-modules.
Archiv der Mathematik,
Vol. 54,
Issue. 4,
p.
340.
Albrecht, Ulrich
1990.
Endomorphism Rings of Faithfully Flat Abelian Groups.
Results in Mathematics,
Vol. 17,
Issue. 3-4,
p.
179.


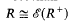 . I present here a partial solution.
. I present here a partial solution.