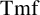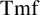1 Introduction
Generalised cohomology theories are powerful tools in algebraic topology, not only in their immediate utility in topology and geometry, but also in their ability to unify various areas of mathematics. The two most prominent examples of such are singular cohomology and topological K-theory, which possess connections to algebra, functional analysis, differential geometry and physics.
In this article, we discuss the cohomology theory
![]() $\operatorname {\mathrm {Tmf}}$
of topological modular forms, a higher order analogue of singular cohomology and topological K-theory. This theory
$\operatorname {\mathrm {Tmf}}$
of topological modular forms, a higher order analogue of singular cohomology and topological K-theory. This theory
![]() $\operatorname {\mathrm {Tmf}}$
possesses connections to number theory and arithmetic geometry through modular forms and the moduli stack of elliptic curves, as well as to string topology and physics through a map from the string bordism groups to the
$\operatorname {\mathrm {Tmf}}$
possesses connections to number theory and arithmetic geometry through modular forms and the moduli stack of elliptic curves, as well as to string topology and physics through a map from the string bordism groups to the
![]() $\operatorname {\mathrm {Tmf}}$
-cohomology of spheres; see [Reference Behrens and MillerBeh20, Reference Douglas, Francis, Henriques and HillDFHH14] for general introductions. Moreover, the recent advances in equivariant topological modular forms [Reference Gepner and MeierGM20, Reference LurieLur19], applications to various computations in homotopy theory [Reference Goerss, Henn, Mahowald and RezkGHMR05, Reference Wang and XuWX17] and conjectural connections to topological field theories [Reference Stolz, Teichner and SatiST11] all suggest that we are still now only scratching the surface of
$\operatorname {\mathrm {Tmf}}$
-cohomology of spheres; see [Reference Behrens and MillerBeh20, Reference Douglas, Francis, Henriques and HillDFHH14] for general introductions. Moreover, the recent advances in equivariant topological modular forms [Reference Gepner and MeierGM20, Reference LurieLur19], applications to various computations in homotopy theory [Reference Goerss, Henn, Mahowald and RezkGHMR05, Reference Wang and XuWX17] and conjectural connections to topological field theories [Reference Stolz, Teichner and SatiST11] all suggest that we are still now only scratching the surface of
![]() $\operatorname {\mathrm {Tmf}}$
.
$\operatorname {\mathrm {Tmf}}$
.
At present, there is a singular definition of
![]() $\operatorname {\mathrm {Tmf}}$
, and that is as the global sections
$\operatorname {\mathrm {Tmf}}$
, and that is as the global sections
![]() $\Gamma (\mathcal {M}_{\mathrm {Ell}},\mathscr {O}^{\mathrm {top}})$
. Here, and elsewhere in this article,
$\Gamma (\mathcal {M}_{\mathrm {Ell}},\mathscr {O}^{\mathrm {top}})$
. Here, and elsewhere in this article,
![]() $\mathcal {M}_{\mathrm {Ell}}$
is the compactification of the moduli stack of elliptic curves and
$\mathcal {M}_{\mathrm {Ell}}$
is the compactification of the moduli stack of elliptic curves and
![]() $\mathscr {O}^{\mathrm {top}}$
is the Goerss–Hopkins–Miller–Lurie sheaf; see [Reference Behrens and MillerBeh20] for more background. For transparency, we remind the reader that the word sheaf is used in a homotopy-theoretic sense, as it takes values in the
$\mathscr {O}^{\mathrm {top}}$
is the Goerss–Hopkins–Miller–Lurie sheaf; see [Reference Behrens and MillerBeh20] for more background. For transparency, we remind the reader that the word sheaf is used in a homotopy-theoretic sense, as it takes values in the
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathbf {E}_\infty $
-rings—the homotopically meaningful environment to study cohomology theories with a highly structured multiplication. The first published construction of this sheaf is due to Behrens [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12], and is based on the unpublished work of Goerss, Hopkins and Miller.
$\mathbf {E}_\infty $
-rings—the homotopically meaningful environment to study cohomology theories with a highly structured multiplication. The first published construction of this sheaf is due to Behrens [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12], and is based on the unpublished work of Goerss, Hopkins and Miller.
One can find variations of this construction in the literature, some using logarithmic geometry on the moduli stack
![]() $\mathcal {M}_{\mathrm {Ell}}$
[Reference Hill and LawsonHL16], and others using oriented derived elliptic curves and p-divisible groups [Reference LurieLur18]. This leads us to a fundamental question:
$\mathcal {M}_{\mathrm {Ell}}$
[Reference Hill and LawsonHL16], and others using oriented derived elliptic curves and p-divisible groups [Reference LurieLur18]. This leads us to a fundamental question:
Are these different constructions in any way compatible?
This question would be easily answered if one could show that
![]() $\mathscr {O}^{\mathrm {top}}$
is the ‘unique’ sheaf with a certain property, assuming this property holds for each competing construction. Moreover, such uniqueness could also be used to further justify the significance of
$\mathscr {O}^{\mathrm {top}}$
is the ‘unique’ sheaf with a certain property, assuming this property holds for each competing construction. Moreover, such uniqueness could also be used to further justify the significance of
![]() $\mathscr {O}^{\mathrm {top}}$
; we leave it to the reader to come to their own conclusions on that front. The property we would like to consider is that of an elliptic cohomology theory.
$\mathscr {O}^{\mathrm {top}}$
; we leave it to the reader to come to their own conclusions on that front. The property we would like to consider is that of an elliptic cohomology theory.
Definition 1.1. Let E be a generalised elliptic curve over a ring R with irreducible geometric fibres, which is equivalent data to a morphism of stacks
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
. We say that a homotopy commutative ring spectrum
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
. We say that a homotopy commutative ring spectrum
![]() $\mathcal {E}$
is an elliptic cohomology theory for E (or
$\mathcal {E}$
is an elliptic cohomology theory for E (or
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
) if we have the following data:
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
) if we have the following data:
-
(1)
 $\mathcal {E}$
is weakly 2-periodic, meaning the homotopy group
$\mathcal {E}$
is weakly 2-periodic, meaning the homotopy group
 $\pi _2 \mathcal {E}$
is a projective
$\pi _2 \mathcal {E}$
is a projective
 $\pi _0 \mathcal {E}$
-module of rank one and for every integer n, the canonical map of
$\pi _0 \mathcal {E}$
-module of rank one and for every integer n, the canonical map of
 $\pi _0\mathcal {E}$
-modules is an isomorphism;
$\pi _0\mathcal {E}$
-modules is an isomorphism; $$ \begin{align*}\pi_2 \mathcal{E}\underset{\pi_0\mathcal{E}}{\otimes} \pi_n \mathcal{E}\to \pi_{n+2}\mathcal{E}\end{align*} $$
$$ \begin{align*}\pi_2 \mathcal{E}\underset{\pi_0\mathcal{E}}{\otimes} \pi_n \mathcal{E}\to \pi_{n+2}\mathcal{E}\end{align*} $$
-
(2) the groups
 $\pi _k \mathcal {E}$
vanish for all odd integers k, so in particular
$\pi _k \mathcal {E}$
vanish for all odd integers k, so in particular
 $\mathcal {E}$
is complex orientable;
$\mathcal {E}$
is complex orientable; -
(3) there is a chosen isomorphism of rings
 $\pi _0 \mathcal {E}\simeq R$
; and
$\pi _0 \mathcal {E}\simeq R$
; and -
(4) there is a chosen isomorphism of formal groups
 $\widehat {E}\simeq \widehat {\mathbf {G}}_{\mathcal {E}}$
over R, between the formal group of E and the classical Quillen formal group of
$\widehat {E}\simeq \widehat {\mathbf {G}}_{\mathcal {E}}$
over R, between the formal group of E and the classical Quillen formal group of
 $\mathcal {E}$
; see [Reference LurieLur18, Section 4].
$\mathcal {E}$
; see [Reference LurieLur18, Section 4].
We say a collection of such
![]() $\mathcal {E}$
is natural if the isomorphisms in parts (3) and (4) above are natural with respect to a specified subcategory of affine schemes over
$\mathcal {E}$
is natural if the isomorphisms in parts (3) and (4) above are natural with respect to a specified subcategory of affine schemes over
![]() $\mathcal {M}_{\mathrm {Ell}}$
. (Other variations of this definition can be found elsewhere in the literature; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.6] or [Reference Lurie and BaasLur09a, Definition 1.2].)
$\mathcal {M}_{\mathrm {Ell}}$
. (Other variations of this definition can be found elsewhere in the literature; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.6] or [Reference Lurie and BaasLur09a, Definition 1.2].)
The following is a simple uniqueness statement for
![]() $\mathscr {O}^{\mathrm {top}}$
as a functor valued in homotopy commutative ring spectra—a much weaker structure than that of an
$\mathscr {O}^{\mathrm {top}}$
as a functor valued in homotopy commutative ring spectra—a much weaker structure than that of an
![]() $\mathbf {E}_\infty $
-ring.
$\mathbf {E}_\infty $
-ring.
Proposition 1.2. The functor
![]() $\mathrm {h}\mathscr {O}^{\mathrm {top}}\colon \mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
, from the small affine étale site
$\mathrm {h}\mathscr {O}^{\mathrm {top}}\colon \mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
, from the small affine étale site
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $\mathcal {M}_{\mathrm {Ell}}$
to the 1-category of homotopy commutative ring spectra, is uniquely defined up to isomorphism by the property that it defines natural elliptic cohomology theories on
$\mathcal {M}_{\mathrm {Ell}}$
to the 1-category of homotopy commutative ring spectra, is uniquely defined up to isomorphism by the property that it defines natural elliptic cohomology theories on
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
The proof of the above statement follows from the fact that each section
![]() $\mathscr {O}^{\mathrm {top}}(R)$
is Landweber exact; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark1.4] for some discussion. A remarkable fact about
$\mathscr {O}^{\mathrm {top}}(R)$
is Landweber exact; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark1.4] for some discussion. A remarkable fact about
![]() $\mathscr {O}^{\mathrm {top}}$
is that the property that it defines natural elliptic cohomology theories actually characterises this sheaf with values in the
$\mathscr {O}^{\mathrm {top}}$
is that the property that it defines natural elliptic cohomology theories actually characterises this sheaf with values in the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {CAlg}}$
of
${\mathrm {CAlg}}$
of
![]() $\mathbf {E}_\infty $
-rings. The following is stated (without proof) in [Reference Lurie and BaasLur09a, Theorem 1.1] and [Reference GoerssGoe10, Theorem 1.2].
$\mathbf {E}_\infty $
-rings. The following is stated (without proof) in [Reference Lurie and BaasLur09a, Theorem 1.1] and [Reference GoerssGoe10, Theorem 1.2].
Theorem 1.3. The sheaf of
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\mathscr {O}^{\mathrm {top}}$
on the small étale site of
$\mathscr {O}^{\mathrm {top}}$
on the small étale site of
![]() $\mathcal {M}_{\mathrm {Ell}}$
is uniquely defined up to homotopy by the property that it defines natural elliptic cohomology theories on the small affine étale site of
$\mathcal {M}_{\mathrm {Ell}}$
is uniquely defined up to homotopy by the property that it defines natural elliptic cohomology theories on the small affine étale site of
![]() $\mathcal {M}_{\mathrm {Ell}}$
. The same holds for the restriction
$\mathcal {M}_{\mathrm {Ell}}$
. The same holds for the restriction
![]() $\mathscr {O}^{\mathrm {top}}_{\mathrm {sm}}$
of
$\mathscr {O}^{\mathrm {top}}_{\mathrm {sm}}$
of
![]() $\mathscr {O}^{\mathrm {top}}$
to the small étale site of
$\mathscr {O}^{\mathrm {top}}$
to the small étale site of
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
, the moduli stack of smooth elliptic curves. (Along the way, we prove similar uniqueness statements for completions of
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
, the moduli stack of smooth elliptic curves. (Along the way, we prove similar uniqueness statements for completions of
![]() $\mathscr {O}^{\mathrm {top}}$
at a prime, its rationalisations as well as localisations as the height
$\mathscr {O}^{\mathrm {top}}$
at a prime, its rationalisations as well as localisations as the height
![]() $1$
and height
$1$
and height
![]() $2$
Morava K-theories.)
$2$
Morava K-theories.)
The difference between Proposition 1.2 and Theorem 1.3 is two-fold: Theorem 1.3 states not only that
![]() $\mathscr {O}^{\mathrm {top}}$
is uniquely defined up to homotopy as a sheaf of
$\mathscr {O}^{\mathrm {top}}$
is uniquely defined up to homotopy as a sheaf of
![]() $\mathbf {E}_\infty $
-rings (as opposed to a diagram in
$\mathbf {E}_\infty $
-rings (as opposed to a diagram in
![]() ${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
), but that statement is made in an
${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
), but that statement is made in an
![]() $\infty $
-category (as opposed to the 1-category
$\infty $
-category (as opposed to the 1-category
![]() ${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
).
${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
).
The utility of Theorem 1.3 is evident. For example, and as indicated above, it retroactively shows that the various constructions of
![]() $\mathscr {O}^{\mathrm {top}}$
found in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12], [Reference Hill and LawsonHL16] and [Reference DaviesDav21, Section 1] (and also [Reference LurieLur18, Section 7], [Reference DaviesDav20, Section 5.3], [Reference DaviesDav22a, Section 6.1] and [Reference DaviesDav22b, Section 1] over the moduli stack of smooth elliptic curves) all agree up to homotopy. Importantly, Theorem 1.3 constructs noncanonical (see Remark 2.2) equivalences of
$\mathscr {O}^{\mathrm {top}}$
found in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12], [Reference Hill and LawsonHL16] and [Reference DaviesDav21, Section 1] (and also [Reference LurieLur18, Section 7], [Reference DaviesDav20, Section 5.3], [Reference DaviesDav22a, Section 6.1] and [Reference DaviesDav22b, Section 1] over the moduli stack of smooth elliptic curves) all agree up to homotopy. Importantly, Theorem 1.3 constructs noncanonical (see Remark 2.2) equivalences of
![]() $\mathbf {E}_\infty $
-rings between all available definitions of
$\mathbf {E}_\infty $
-rings between all available definitions of
![]() $\operatorname {\mathrm {Tmf}}$
; a conclusion which does not follow directly from Proposition 1.2. The author also finds the proof long and complex enough to warrant a publicly available write-up.
$\operatorname {\mathrm {Tmf}}$
; a conclusion which does not follow directly from Proposition 1.2. The author also finds the proof long and complex enough to warrant a publicly available write-up.
1.1 Outline
To prove Theorem 1.3, we first reduce the question to one of the connectedness of a certain moduli space; see Section 2. In Section 3, we formulate and prove a statement about spaces of natural transformations which we often use; we suggest that the reader initially skips this section and only returns when they deem it necessary. Our proof of Theorem 1.3 (reformulated as Theorem 2.1) occurs in Section 4, and follows Behrens’ construction of
![]() $\operatorname {\mathrm {Tmf}}$
rather closely: first, we work with the separate chromatic layers, before gluing things together in both a transchromatic sense and then an arithmetic sense. The
$\operatorname {\mathrm {Tmf}}$
rather closely: first, we work with the separate chromatic layers, before gluing things together in both a transchromatic sense and then an arithmetic sense. The
![]() $K(1)$
-local case in this section requires a statement about p-adic Adams operations on p-adic K-theory, which is the focus of our final technical Section 5.
$K(1)$
-local case in this section requires a statement about p-adic Adams operations on p-adic K-theory, which is the focus of our final technical Section 5.
1.2 Conventions
We assume that the reader is familiar with the language of
![]() $\infty $
-categories as well as the techniques used in the construction of
$\infty $
-categories as well as the techniques used in the construction of
![]() $\mathscr {O}^{\mathrm {top}}$
as described by Behrens [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12]. Furthermore, we advise the reader keeps a copy of idem in their vicinity. Write
$\mathscr {O}^{\mathrm {top}}$
as described by Behrens [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12]. Furthermore, we advise the reader keeps a copy of idem in their vicinity. Write
![]() $\operatorname {\mathrm {Map}}_{\mathcal {C}}(X,Y)$
for the mapping space between any two objects
$\operatorname {\mathrm {Map}}_{\mathcal {C}}(X,Y)$
for the mapping space between any two objects
![]() $X,Y$
in an
$X,Y$
in an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
, and
$\mathcal {C}$
, and
![]() $\mathrm {Hom}_{\mathrm {h}\mathcal {C}}(X,Y)$
for its zeroth truncation, or equivalently, for
$\mathrm {Hom}_{\mathrm {h}\mathcal {C}}(X,Y)$
for its zeroth truncation, or equivalently, for
![]() $\pi _0\operatorname {\mathrm {Map}}_{\mathcal {C}}(X,Y)$
. Let us also suppress the notation distinguishing a 1-category from its nerve, considered as an
$\pi _0\operatorname {\mathrm {Map}}_{\mathcal {C}}(X,Y)$
. Let us also suppress the notation distinguishing a 1-category from its nerve, considered as an
![]() $\infty $
-category, and the same for a 2-category, such as the small étale site over
$\infty $
-category, and the same for a 2-category, such as the small étale site over
![]() $\mathcal {M}_{\mathrm {Ell}}$
; see [Reference LurieLur, Tag 007J].
$\mathcal {M}_{\mathrm {Ell}}$
; see [Reference LurieLur, Tag 007J].
2 A reformulation
Let us now make a statement to help us prove Theorem 1.3.
Theorem 2.1. Write
![]() $\mathcal {U}$
(respectively
$\mathcal {U}$
(respectively
![]() $\mathcal {U}_{\mathrm {sm}}$
) for the (2-) category of affine schemes with étale maps to
$\mathcal {U}_{\mathrm {sm}}$
) for the (2-) category of affine schemes with étale maps to
![]() $\mathcal {M}_{\mathrm {Ell}}$
(respectively
$\mathcal {M}_{\mathrm {Ell}}$
(respectively
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
). Then the spaces
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
). Then the spaces
 $$ \begin{align*}\mathcal{Z}&=\operatorname{\mathrm{Fun}}(\mathcal{U}^{\mathrm{op}}, {\mathrm{CAlg}})\underset{\operatorname{\mathrm{Fun}}(\mathcal{U}^{\mathrm{op}}, {\mathrm{CAlg}}(\mathrm{h}\mathrm{Sp}))}{\times} \{\mathrm{h}\mathscr{O}^{\mathrm{top}}\}\\ \mathcal{Z}^{\mathrm{sm}}&=\operatorname{\mathrm{Fun}}(\mathcal{U}_{\mathrm{sm}}^{\mathrm{op}}, {\mathrm{CAlg}})\underset{\operatorname{\mathrm{Fun}}(\mathcal{U}_{\mathrm{sm}}^{\mathrm{op}}, {\mathrm{CAlg}}(\mathrm{h}\mathrm{Sp}))}{\times} \{\mathrm{h}\mathscr{O}^{\mathrm{top}}\}\end{align*} $$
$$ \begin{align*}\mathcal{Z}&=\operatorname{\mathrm{Fun}}(\mathcal{U}^{\mathrm{op}}, {\mathrm{CAlg}})\underset{\operatorname{\mathrm{Fun}}(\mathcal{U}^{\mathrm{op}}, {\mathrm{CAlg}}(\mathrm{h}\mathrm{Sp}))}{\times} \{\mathrm{h}\mathscr{O}^{\mathrm{top}}\}\\ \mathcal{Z}^{\mathrm{sm}}&=\operatorname{\mathrm{Fun}}(\mathcal{U}_{\mathrm{sm}}^{\mathrm{op}}, {\mathrm{CAlg}})\underset{\operatorname{\mathrm{Fun}}(\mathcal{U}_{\mathrm{sm}}^{\mathrm{op}}, {\mathrm{CAlg}}(\mathrm{h}\mathrm{Sp}))}{\times} \{\mathrm{h}\mathscr{O}^{\mathrm{top}}\}\end{align*} $$
are connected.
Remark 2.2. As mentioned in [Reference LurieLur18, Remark 7.0.2], the moduli space
![]() $\mathcal {Z}^{\mathrm {sm}}$
is not contractible. In other words, Theorem 2.1 states that
$\mathcal {Z}^{\mathrm {sm}}$
is not contractible. In other words, Theorem 2.1 states that
![]() $\mathscr {O}^{\mathrm {top}}$
is unique as a
$\mathscr {O}^{\mathrm {top}}$
is unique as a
![]() ${\mathrm {CAlg}}$
-valued presheaf of elliptic cohomology theories on
${\mathrm {CAlg}}$
-valued presheaf of elliptic cohomology theories on
![]() $\mathcal {U}^{\mathrm {sm}}$
only up to homotopy, and does not claim anything more about the contractibility of this space. We would like to guide the reader to an explanation of this fact given by Tyler Lawson on mathoverflow.net; see [Reference LawsonLaw].
$\mathcal {U}^{\mathrm {sm}}$
only up to homotopy, and does not claim anything more about the contractibility of this space. We would like to guide the reader to an explanation of this fact given by Tyler Lawson on mathoverflow.net; see [Reference LawsonLaw].
Proof of Theorem 1.3 from Theorem 2.1. The
![]() $\infty $
-category of sheaves of
$\infty $
-category of sheaves of
![]() $\mathbf {E}_\infty $
-rings on the étale site of
$\mathbf {E}_\infty $
-rings on the étale site of
![]() $\mathcal {M}_{\mathrm {Ell}}$
is equivalent, by restriction and right Kan extension, to the
$\mathcal {M}_{\mathrm {Ell}}$
is equivalent, by restriction and right Kan extension, to the
![]() $\infty $
-category of sheaves of
$\infty $
-category of sheaves of
![]() $\mathbf {E}_\infty $
-rings on the affine étale site of
$\mathbf {E}_\infty $
-rings on the affine étale site of
![]() $\mathcal {M}_{\mathrm {Ell}}$
; see [Reference DaviesDav22a, Lemma 6.1.10] for a similar argument following the ‘comparison lemma’ of [Reference HoyoisHoy14, Lemma C.3]. Note that the latter is an
$\mathcal {M}_{\mathrm {Ell}}$
; see [Reference DaviesDav22a, Lemma 6.1.10] for a similar argument following the ‘comparison lemma’ of [Reference HoyoisHoy14, Lemma C.3]. Note that the latter is an
![]() $\infty $
-subcategory of
$\infty $
-subcategory of
![]() $\operatorname {\mathrm {Fun}}(\mathcal {U}^{\mathrm {op}},{\mathrm {CAlg}})$
, and that if a functor
$\operatorname {\mathrm {Fun}}(\mathcal {U}^{\mathrm {op}},{\mathrm {CAlg}})$
, and that if a functor
![]() $F\colon \mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}$
defines natural elliptic cohomology theories and there is an equivalence
$F\colon \mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}$
defines natural elliptic cohomology theories and there is an equivalence
![]() $F\simeq G$
, then G also defines natural elliptic cohomology theories. These two observations show that it suffices to prove the space
$F\simeq G$
, then G also defines natural elliptic cohomology theories. These two observations show that it suffices to prove the space
![]() $\mathcal {Z}'$
is connected, where
$\mathcal {Z}'$
is connected, where
![]() $\mathcal {Z}'$
is the component of
$\mathcal {Z}'$
is the component of
![]() $\operatorname {\mathrm {Fun}}(\mathcal {U}^{\mathrm {op}}, {\mathrm {CAlg}})^\simeq $
spanned by those functors which define natural elliptic cohomology theories. There is a map
$\operatorname {\mathrm {Fun}}(\mathcal {U}^{\mathrm {op}}, {\mathrm {CAlg}})^\simeq $
spanned by those functors which define natural elliptic cohomology theories. There is a map
![]() $\mathcal {Z}\to \mathcal {Z}'$
as both
$\mathcal {Z}\to \mathcal {Z}'$
as both
![]() $\mathscr {O}^{\mathrm {top}}$
and any presheaf of
$\mathscr {O}^{\mathrm {top}}$
and any presheaf of
![]() $\mathbf {E}_\infty $
-rings, equivalent to
$\mathbf {E}_\infty $
-rings, equivalent to
![]() $\mathscr {O}^{\mathrm {top}}$
as a diagram of homotopy commutative ring spectra, define natural elliptic cohomology theories. The map
$\mathscr {O}^{\mathrm {top}}$
as a diagram of homotopy commutative ring spectra, define natural elliptic cohomology theories. The map
![]() $\mathcal {Z}\to \mathcal {Z}'$
induces an equivalence on
$\mathcal {Z}\to \mathcal {Z}'$
induces an equivalence on
![]() $\pi _0$
as [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 1.6] states that any functor
$\pi _0$
as [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 1.6] states that any functor
![]() $\mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
which defines natural elliptic cohomology theories is isomorphic to
$\mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
which defines natural elliptic cohomology theories is isomorphic to
![]() $\mathrm {h}\mathscr {O}^{\mathrm {top}}$
. (The argument outlined in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 1.4] is stated for
$\mathrm {h}\mathscr {O}^{\mathrm {top}}$
. (The argument outlined in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 1.4] is stated for
![]() $\mathrm {h}\mathrm {Sp}$
, but the statement can be modified for
$\mathrm {h}\mathrm {Sp}$
, but the statement can be modified for
![]() ${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
. Indeed, the crucial fact is that there are no phantom maps between Landweber exact spectra, meaning the functor from
${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
. Indeed, the crucial fact is that there are no phantom maps between Landweber exact spectra, meaning the functor from
![]() $\mathrm {h}\mathrm {Sp}$
to the 1-category of generalised cohomology theories is fully faithful on such spectra. The analogous fact in the multiplicative context follows, meaning the functor from
$\mathrm {h}\mathrm {Sp}$
to the 1-category of generalised cohomology theories is fully faithful on such spectra. The analogous fact in the multiplicative context follows, meaning the functor from
![]() ${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
to the 1-category of multiplicative cohomology theories is fully faithful on Landweber exact homotopy commutative ring spectra.) Theorem 2.1 then implies that the moduli space
${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
to the 1-category of multiplicative cohomology theories is fully faithful on Landweber exact homotopy commutative ring spectra.) Theorem 2.1 then implies that the moduli space
![]() $\mathcal {Z}'$
is also connected. The same argument can be made for
$\mathcal {Z}'$
is also connected. The same argument can be made for
![]() $\mathcal {Z}^{\mathrm {sm}}$
.
$\mathcal {Z}^{\mathrm {sm}}$
.
Remark 2.3. Write
![]() $\mathcal {U}_{\mathbf {Q}}$
for the small affine étale site of
$\mathcal {U}_{\mathbf {Q}}$
for the small affine étale site of
![]() $\mathcal {M}_{\mathrm {Ell}}\times \operatorname {\mathrm {Spec}} \mathbf {Q}$
and for each prime p, write
$\mathcal {M}_{\mathrm {Ell}}\times \operatorname {\mathrm {Spec}} \mathbf {Q}$
and for each prime p, write
![]() $\mathcal {U}_p$
for the small affine étale site of
$\mathcal {U}_p$
for the small affine étale site of
![]() $\mathcal {M}_{\mathrm {Ell}}\times \operatorname {\mathrm {Spf}} \mathbf {Z}_p$
. The construction of
$\mathcal {M}_{\mathrm {Ell}}\times \operatorname {\mathrm {Spf}} \mathbf {Z}_p$
. The construction of
![]() $\mathscr {O}^{\mathrm {top}}$
, as found in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12] for example, proceeds first with a rational construction
$\mathscr {O}^{\mathrm {top}}$
, as found in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12] for example, proceeds first with a rational construction
![]() $\mathscr {O}^{\mathrm {top}}_{\mathbf {Q}}$
over
$\mathscr {O}^{\mathrm {top}}_{\mathbf {Q}}$
over
![]() $\mathcal {U}_{\mathbf {Q}}$
, and a p-complete construction
$\mathcal {U}_{\mathbf {Q}}$
, and a p-complete construction
![]() $\mathscr {O}^{\mathrm {top}}_p$
over
$\mathscr {O}^{\mathrm {top}}_p$
over
![]() $\mathcal {U}_p$
. The methods of our proof for Theorem 2.1 show that the moduli spaces
$\mathcal {U}_p$
. The methods of our proof for Theorem 2.1 show that the moduli spaces
![]() $\mathcal {Z}_{\mathbf {Q}}$
and
$\mathcal {Z}_{\mathbf {Q}}$
and
![]() $\mathcal {Z}_p$
, of realisations of
$\mathcal {Z}_p$
, of realisations of
![]() $\mathrm {h}\mathscr {O}^{\mathrm {top}}_{\mathbf {Q}}$
and
$\mathrm {h}\mathscr {O}^{\mathrm {top}}_{\mathbf {Q}}$
and
![]() $\mathrm {h}\mathscr {O}^{\mathrm {top}}_p$
over these aforementioned sites, are also connected. This means that analogues of Theorem 1.3 also hold for both
$\mathrm {h}\mathscr {O}^{\mathrm {top}}_p$
over these aforementioned sites, are also connected. This means that analogues of Theorem 1.3 also hold for both
![]() $\mathscr {O}^{\mathrm {top}}_{\mathbf {Q}}$
and
$\mathscr {O}^{\mathrm {top}}_{\mathbf {Q}}$
and
![]() $\mathscr {O}^{\mathrm {top}}_p$
. The same hold for the p-complete and rational version of
$\mathscr {O}^{\mathrm {top}}_p$
. The same hold for the p-complete and rational version of
![]() $\mathscr {O}^{\mathrm {top}}_{\mathrm {sm}}$
for similar reasons. Moreover, following the ‘arithmetic compatibility’ discussed in the proof of Theorem 2.1, it follows that the localisations
$\mathscr {O}^{\mathrm {top}}_{\mathrm {sm}}$
for similar reasons. Moreover, following the ‘arithmetic compatibility’ discussed in the proof of Theorem 2.1, it follows that the localisations
![]() $\mathscr {O}^{\mathrm {top}}[\mathcal {P}^{-1}]$
and
$\mathscr {O}^{\mathrm {top}}[\mathcal {P}^{-1}]$
and
![]() $\mathscr {O}_{\mathrm {sm}}^{\mathrm {top}}[\mathcal {P}^{-1}]$
satisfy their own version of Theorem 1.3, where
$\mathscr {O}_{\mathrm {sm}}^{\mathrm {top}}[\mathcal {P}^{-1}]$
satisfy their own version of Theorem 1.3, where
![]() $\mathcal {P}$
is any set of primes.
$\mathcal {P}$
is any set of primes.
The following is a short remark on the homotopy groups of elliptic cohomology theories which is important later.
Remark 2.4. Let
![]() $\mathcal {E}$
be an elliptic cohomology theory for some
$\mathcal {E}$
be an elliptic cohomology theory for some
![]() $E\colon {\kern-2pt}\operatorname {\mathrm {Spec}} R{\kern-1pt}\to{\kern-1pt} \mathcal {M}_{\mathrm {Ell}}$
. It follows that there is a natural isomorphism
$E\colon {\kern-2pt}\operatorname {\mathrm {Spec}} R{\kern-1pt}\to{\kern-1pt} \mathcal {M}_{\mathrm {Ell}}$
. It follows that there is a natural isomorphism
![]() $\pi _{2k}\mathcal {E}\simeq \omega _E^{\otimes k}$
for all integers k, where
$\pi _{2k}\mathcal {E}\simeq \omega _E^{\otimes k}$
for all integers k, where
![]() $\omega _E$
is the dualising line for the formal group
$\omega _E$
is the dualising line for the formal group
![]() $\widehat {E}$
; see [Reference LurieLur18, Section 4.2]. Indeed, as the odd homotopy groups of
$\widehat {E}$
; see [Reference LurieLur18, Section 4.2]. Indeed, as the odd homotopy groups of
![]() $\mathcal {E}$
vanish, we see
$\mathcal {E}$
vanish, we see
![]() $\mathcal {E}$
possesses a complex orientation that yields the classical Quillen formal group
$\mathcal {E}$
possesses a complex orientation that yields the classical Quillen formal group
![]() $\widehat {\mathbf {G}}_{\mathcal {E}}^{\mathcal {Q}_0}$
over
$\widehat {\mathbf {G}}_{\mathcal {E}}^{\mathcal {Q}_0}$
over
![]() $\pi _0 \mathcal {E}$
; see [Reference LurieLur18, Example 4.1.2], for example. From this, we see
$\pi _0 \mathcal {E}$
; see [Reference LurieLur18, Example 4.1.2], for example. From this, we see
![]() $\mathcal {E}$
is complex periodic, meaning it has a complex orientation and is weakly 2-periodic (see [Reference LurieLur18, Section 4.1]), and [Reference LurieLur18, Example 4.2.19] then implies that
$\mathcal {E}$
is complex periodic, meaning it has a complex orientation and is weakly 2-periodic (see [Reference LurieLur18, Section 4.1]), and [Reference LurieLur18, Example 4.2.19] then implies that
![]() $\pi _2\mathcal {E}$
is isomorphic to the dualising line for the formal group
$\pi _2\mathcal {E}$
is isomorphic to the dualising line for the formal group
![]() $\widehat {\mathbf {G}}_{\mathcal {E}}^{\mathcal {Q}_0}$
. Part (4) of Definition 1.1 states that
$\widehat {\mathbf {G}}_{\mathcal {E}}^{\mathcal {Q}_0}$
. Part (4) of Definition 1.1 states that
![]() $\pi _2\mathcal {E}$
is naturally isomorphic to
$\pi _2\mathcal {E}$
is naturally isomorphic to
![]() $\omega _E$
, and part (1) gives us the claim above.
$\omega _E$
, and part (1) gives us the claim above.
3 Spaces of natural transformations
To prove Theorem 2.1, we show that any two functors
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {O}'$
in
$\mathscr {O}'$
in
![]() $\mathcal {Z}$
can be connected by a path in
$\mathcal {Z}$
can be connected by a path in
![]() $\mathcal {Z}$
. In particular, we would like effective tools for studying spaces of natural transformations between functors of
$\mathcal {Z}$
. In particular, we would like effective tools for studying spaces of natural transformations between functors of
![]() $\infty $
-categories. The following is known to experts, and a model categorical interpretation can be found in [Reference Dwyer, Kan and SmithDKS89].
$\infty $
-categories. The following is known to experts, and a model categorical interpretation can be found in [Reference Dwyer, Kan and SmithDKS89].
Proposition 3.1. Let
![]() $\mathcal {C},\mathcal {D}$
be
$\mathcal {C},\mathcal {D}$
be
![]() $\infty $
-categories and
$\infty $
-categories and
![]() $F,G\colon \mathcal {C}\to \mathcal {D}$
be functors. Suppose that for all objects
$F,G\colon \mathcal {C}\to \mathcal {D}$
be functors. Suppose that for all objects
![]() $X,Y$
in
$X,Y$
in
![]() $\mathcal {C}$
, the mapping space
$\mathcal {C}$
, the mapping space
![]() $\operatorname {\mathrm {Map}}_{\mathcal {D}}(FX,GY)$
is discrete, meaning the natural map
$\operatorname {\mathrm {Map}}_{\mathcal {D}}(FX,GY)$
is discrete, meaning the natural map
is an equivalence of spaces. Then the mapping space
![]() $\operatorname {\mathrm {Map}}_{\operatorname {\mathrm {Fun}}(\mathcal {C},\mathcal {D})}(F,G)$
is also discrete, so the natural map
$\operatorname {\mathrm {Map}}_{\operatorname {\mathrm {Fun}}(\mathcal {C},\mathcal {D})}(F,G)$
is also discrete, so the natural map
is an equivalence of spaces, where an
![]() $\mathrm {h}$
before a functor denotes post-composition with the unit map
$\mathrm {h}$
before a functor denotes post-composition with the unit map
![]() $\mathcal {D}\to \mathrm {h}\mathcal {D}$
of the homotopy category-nerve adjunction of [Reference LurieLur09b, Proposition 1.2.3.1].
$\mathcal {D}\to \mathrm {h}\mathcal {D}$
of the homotopy category-nerve adjunction of [Reference LurieLur09b, Proposition 1.2.3.1].
Proof. By [Reference Gepner, Haugseng and NikolausGHN17, Proposition 5.1], the space of natural transformations from F to G is naturally equivalent to the limit of the diagram
where
![]() $\operatorname {\mathrm {Tw}}(\mathcal {C})$
is the twisted arrow category of
$\operatorname {\mathrm {Tw}}(\mathcal {C})$
is the twisted arrow category of
![]() $\mathcal {C}$
(see [Reference Gepner, Haugseng and NikolausGHN17, Definition 2.2]), and the
$\mathcal {C}$
(see [Reference Gepner, Haugseng and NikolausGHN17, Definition 2.2]), and the
![]() $\operatorname {\mathrm {Tw}}(\mathcal {C})\to \mathcal {C}\times \mathcal {C}^{\mathrm {op}}$
is the natural right fibration (see idem). (We stick to the notation and conventions of [Reference Gepner, Haugseng and NikolausGHN17], which is a particular choice out of a possible two; see [Reference Gepner, Haugseng and NikolausGHN17, Warning 2.4].) The limit of Equation (3-1) is, by definition, the end of the composition
$\operatorname {\mathrm {Tw}}(\mathcal {C})\to \mathcal {C}\times \mathcal {C}^{\mathrm {op}}$
is the natural right fibration (see idem). (We stick to the notation and conventions of [Reference Gepner, Haugseng and NikolausGHN17], which is a particular choice out of a possible two; see [Reference Gepner, Haugseng and NikolausGHN17, Warning 2.4].) The limit of Equation (3-1) is, by definition, the end of the composition
![]() $\mathcal {C}^{\mathrm {op}}\times \mathcal {C}\to \mathcal {S}$
. Consider the following not a priori commutative diagram of
$\mathcal {C}^{\mathrm {op}}\times \mathcal {C}\to \mathcal {S}$
. Consider the following not a priori commutative diagram of
![]() $\infty $
-categories:
$\infty $
-categories:

Above, the vertical functors are the obvious ones, and hence the left and middle squares commute. Additionally,
![]() $\mathcal {S}_{\leq 0}\subseteq \mathcal {S}$
denotes the
$\mathcal {S}_{\leq 0}\subseteq \mathcal {S}$
denotes the
![]() $\infty $
-category of discrete spaces. Our hypotheses dictate that the dashed arrow above exists, which we now denote by P, such that the upper-right and lower-left triangles commute. As the inclusion of
$\infty $
-category of discrete spaces. Our hypotheses dictate that the dashed arrow above exists, which we now denote by P, such that the upper-right and lower-left triangles commute. As the inclusion of
![]() $\infty $
-subcategories
$\infty $
-subcategories
![]() $\mathcal {S}_{\leq 0}\subseteq \mathcal {S}$
preserves limits, we note it suffices to compute the limit of Equation (3-1) as the limit of
$\mathcal {S}_{\leq 0}\subseteq \mathcal {S}$
preserves limits, we note it suffices to compute the limit of Equation (3-1) as the limit of
![]() $P\circ T$
inside
$P\circ T$
inside
![]() $\mathcal {S}_{\leq 0}$
. As this limit lands in
$\mathcal {S}_{\leq 0}$
. As this limit lands in
![]() $\mathcal {S}_{\leq 0}$
, which is equivalent to the nerve of the 1-category of sets, we see the limit of
$\mathcal {S}_{\leq 0}$
, which is equivalent to the nerve of the 1-category of sets, we see the limit of
![]() $P\circ T$
can be calculated as the limit of the lower-horizontal composition of Equation (3-2). We then obtain the following natural equivalences, twice employing [Reference Gepner, Haugseng and NikolausGHN17, Proposition 5.1], first for general
$P\circ T$
can be calculated as the limit of the lower-horizontal composition of Equation (3-2). We then obtain the following natural equivalences, twice employing [Reference Gepner, Haugseng and NikolausGHN17, Proposition 5.1], first for general
![]() $\infty $
-categories, and again in the classical 1-categorical case:
$\infty $
-categories, and again in the classical 1-categorical case:
 $$ \begin{align*}&\,\operatorname{\mathrm{Map}}_{\operatorname{\mathrm{Fun}}(\mathcal{C},\mathcal{D})}(F,G)\simeq \underset{\operatorname{\mathrm{Tw}}(\mathcal{C})}{{\mathrm{lim}\,}} M (F^{\mathrm{op}}\times G) T\simeq \underset{\operatorname{\mathrm{Tw}}(\mathcal{C})}{{\mathrm{lim}\,}} PT\\&\simeq \underset{\operatorname{\mathrm{Tw}}(\mathrm{h}\mathcal{C})}{{\mathrm{lim}\,}} H (\mathrm{h} F^{\mathrm{op}}\times \mathrm{h} G)T'\simeq \mathrm{Hom}_{\operatorname{\mathrm{Fun}}(\mathrm{h}\mathcal{C},\mathrm{h}\mathcal{D})}(\mathrm{h} F,\mathrm{h} G).\end{align*} $$
$$ \begin{align*}&\,\operatorname{\mathrm{Map}}_{\operatorname{\mathrm{Fun}}(\mathcal{C},\mathcal{D})}(F,G)\simeq \underset{\operatorname{\mathrm{Tw}}(\mathcal{C})}{{\mathrm{lim}\,}} M (F^{\mathrm{op}}\times G) T\simeq \underset{\operatorname{\mathrm{Tw}}(\mathcal{C})}{{\mathrm{lim}\,}} PT\\&\simeq \underset{\operatorname{\mathrm{Tw}}(\mathrm{h}\mathcal{C})}{{\mathrm{lim}\,}} H (\mathrm{h} F^{\mathrm{op}}\times \mathrm{h} G)T'\simeq \mathrm{Hom}_{\operatorname{\mathrm{Fun}}(\mathrm{h}\mathcal{C},\mathrm{h}\mathcal{D})}(\mathrm{h} F,\mathrm{h} G).\end{align*} $$
The final (discrete) space above is naturally equivalent to
![]() $\mathrm {Hom}_{\operatorname {\mathrm {Fun}}(\mathcal {C},\mathrm {h}\mathcal {D})}(\mathrm {h} F, \mathrm {h} G)$
from the natural equivalence of
$\mathrm {Hom}_{\operatorname {\mathrm {Fun}}(\mathcal {C},\mathrm {h}\mathcal {D})}(\mathrm {h} F, \mathrm {h} G)$
from the natural equivalence of
![]() $\infty $
-categories
$\infty $
-categories
![]() $\operatorname {\mathrm {Fun}}(\mathcal {C},\mathrm {h}\mathcal {D})\simeq \operatorname {\mathrm {Fun}}(\mathrm {h}\mathcal {C},\mathrm {h}\mathcal {D})$
.
$\operatorname {\mathrm {Fun}}(\mathcal {C},\mathrm {h}\mathcal {D})\simeq \operatorname {\mathrm {Fun}}(\mathrm {h}\mathcal {C},\mathrm {h}\mathcal {D})$
.
4 The proof of Theorem 2.1
Let
![]() $\mathscr {O}\colon \mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}$
be an object of
$\mathscr {O}\colon \mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}$
be an object of
![]() $\mathcal {Z}$
. Hence, it comes equipped with an equivalence
$\mathcal {Z}$
. Hence, it comes equipped with an equivalence
![]() $\mathrm {h}\phi \colon \mathrm {h}\mathscr {O}^{\mathrm {top}}\to \mathrm {h}\mathscr {O}$
of functors
$\mathrm {h}\phi \colon \mathrm {h}\mathscr {O}^{\mathrm {top}}\to \mathrm {h}\mathscr {O}$
of functors
![]() $\mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
. To see
$\mathcal {U}^{\mathrm {op}}\to {\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
. To see
![]() $\mathcal {Z}$
is connected, it suffices to show
$\mathcal {Z}$
is connected, it suffices to show
![]() $\mathrm {h}\phi $
can be lifted to an equivalence
$\mathrm {h}\phi $
can be lifted to an equivalence
![]() $\phi \colon \mathscr {O}^{\mathrm {top}}\to \mathscr {O}$
of presheaves of
$\phi \colon \mathscr {O}^{\mathrm {top}}\to \mathscr {O}$
of presheaves of
![]() $\mathbf {E}_\infty $
-rings on
$\mathbf {E}_\infty $
-rings on
![]() $\mathcal {U}$
. Fix such an
$\mathcal {U}$
. Fix such an
![]() $\mathrm {h}\phi $
for the remainder of this proof. Let us work section-wise, so we also fix an object
$\mathrm {h}\phi $
for the remainder of this proof. Let us work section-wise, so we also fix an object
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
inside
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
inside
![]() $\mathcal {U}$
, and write
$\mathcal {U}$
, and write
for the given natural equivalence of homotopy commutative ring spectra. To naturally lift this map to one of
![]() $\mathbf {E}_\infty $
-rings, we work through the layers of chromatic homotopy theory. This means we first work
$\mathbf {E}_\infty $
-rings, we work through the layers of chromatic homotopy theory. This means we first work
![]() $K(2)$
-locally,
$K(2)$
-locally,
![]() $K(1)$
-locally and then
$K(1)$
-locally and then
![]() $K(0)$
-locally, where
$K(0)$
-locally, where
![]() $K(n)$
denotes the nth Morava K-theory spectrum at a prime p, before gluing these cases together with a p-complete statement followed by an arithmetic statement.
$K(n)$
denotes the nth Morava K-theory spectrum at a prime p, before gluing these cases together with a p-complete statement followed by an arithmetic statement.
In what follows, we write
![]() $(-)_{K(n)}$
for the
$(-)_{K(n)}$
for the
![]() $K(n)$
-localisation of
$K(n)$
-localisation of
![]() $\mathbf {E}_\infty $
-rings, and this notation is also used for the post-composition of a presheaf into
$\mathbf {E}_\infty $
-rings, and this notation is also used for the post-composition of a presheaf into
![]() ${\mathrm {CAlg}}$
with the
${\mathrm {CAlg}}$
with the
![]() $K(n)$
-localisation functor.
$K(n)$
-localisation functor.
 $K(2)$
-local case.
$K(2)$
-local case.
Writing
![]() $\widehat {(-)}$
for base-change over
$\widehat {(-)}$
for base-change over
![]() $\operatorname {\mathrm {Spf}}\mathbf {Z}_p$
, we define
$\operatorname {\mathrm {Spf}}\mathbf {Z}_p$
, we define
![]() $\operatorname {\mathrm {Spf}} R^{\mathrm {ss}}\to \mathcal {M}_{\mathrm {Ell}}^{\mathrm {ss}}$
as the base-change of
$\operatorname {\mathrm {Spf}} R^{\mathrm {ss}}\to \mathcal {M}_{\mathrm {Ell}}^{\mathrm {ss}}$
as the base-change of
![]() $\operatorname {\mathrm {Spf}} \widehat {R}\to \widehat {\mathcal {M}}_{\mathrm {Ell}}$
over
$\operatorname {\mathrm {Spf}} \widehat {R}\to \widehat {\mathcal {M}}_{\mathrm {Ell}}$
over
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ss}}$
, where the latter is the completion of
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ss}}$
, where the latter is the completion of
![]() $\widehat {\mathcal {M}}_{\mathrm {Ell}}$
at the moduli stack
$\widehat {\mathcal {M}}_{\mathrm {Ell}}$
at the moduli stack
![]() $\mathcal {M}_{\mathrm {Ell},\mathbf {F}_p}^{\mathrm {ss}}$
of supersingular elliptic curves over
$\mathcal {M}_{\mathrm {Ell},\mathbf {F}_p}^{\mathrm {ss}}$
of supersingular elliptic curves over
![]() $\mathbf {F}_p$
. This pullback
$\mathbf {F}_p$
. This pullback
![]() $\operatorname {\mathrm {Spf}} R^{\mathrm {ss}}$
is affine by [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 8.7]. Write
$\operatorname {\mathrm {Spf}} R^{\mathrm {ss}}$
is affine by [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 8.7]. Write
![]() $E^{\mathrm {ss}}$
for the elliptic curve defined by
$E^{\mathrm {ss}}$
for the elliptic curve defined by
![]() $\operatorname {\mathrm {Spf}} R^{\mathrm {ss}}\to \mathcal {M}_{\mathrm {Ell}}^{\mathrm {ss}}$
. Serre–Tate and Lubin–Tate theories yield another description of
$\operatorname {\mathrm {Spf}} R^{\mathrm {ss}}\to \mathcal {M}_{\mathrm {Ell}}^{\mathrm {ss}}$
. Serre–Tate and Lubin–Tate theories yield another description of
![]() $R^{\mathrm {ss}}$
. Indeed, as
$R^{\mathrm {ss}}$
. Indeed, as
![]() $\mathcal {M}^{\mathrm {ss}}_{\mathrm {Ell},\mathbf {F}_p}$
is zero-dimensional and smooth over
$\mathcal {M}^{\mathrm {ss}}_{\mathrm {Ell},\mathbf {F}_p}$
is zero-dimensional and smooth over
![]() $\operatorname {\mathrm {Spec}} \mathbf {F}_p$
, it follows that
$\operatorname {\mathrm {Spec}} \mathbf {F}_p$
, it follows that
![]() $\operatorname {\mathrm {Spec}} R^{\mathrm {ss}}/I$
is étale over
$\operatorname {\mathrm {Spec}} R^{\mathrm {ss}}/I$
is étale over
![]() $\mathbf {F}_p$
, where I is the finitely generated ideal generating the topology on
$\mathbf {F}_p$
, where I is the finitely generated ideal generating the topology on
![]() $R^{\mathrm {ss}}$
. This implies
$R^{\mathrm {ss}}$
. This implies
![]() $R^{\mathrm {ss}}/I$
splits as a finite product
$R^{\mathrm {ss}}/I$
splits as a finite product
![]() $\prod _i \kappa _i$
where each
$\prod _i \kappa _i$
where each
![]() $\kappa _i$
is a finite field of characteristic p. This provides a splitting of
$\kappa _i$
is a finite field of characteristic p. This provides a splitting of
![]() $E_0$
, the reduction of
$E_0$
, the reduction of
![]() $E^{\mathrm {ss}}$
over
$E^{\mathrm {ss}}$
over
![]() $R/I$
, into
$R/I$
, into
![]() $E_0\simeq \coprod E_0^i$
. Writing
$E_0\simeq \coprod E_0^i$
. Writing
![]() for the universal deformation ring of the pair
for the universal deformation ring of the pair
![]() $(\kappa _i, \widehat {E}^i_0)$
with associated universal formal group
$(\kappa _i, \widehat {E}^i_0)$
with associated universal formal group
![]() $\widehat {E}^{\mathrm {ss}}_{R_i}$
, we obtain a natural equivalence
$\widehat {E}^{\mathrm {ss}}_{R_i}$
, we obtain a natural equivalence
![]() $R^{\mathrm {ss}}\simeq \prod _i R_i$
as
$R^{\mathrm {ss}}\simeq \prod _i R_i$
as
![]() $E^{\mathrm {ss}}{\colon} {\mathrm{Spf}} R^{\mathrm {ss}}\to \mathcal {M}_{\mathrm {Ell}}^{\mathrm {ss}}$
was étale; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Corollary 4.3].
$E^{\mathrm {ss}}{\colon} {\mathrm{Spf}} R^{\mathrm {ss}}\to \mathcal {M}_{\mathrm {Ell}}^{\mathrm {ss}}$
was étale; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Corollary 4.3].
By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 4.4], the
![]() $K(2)$
-localisations
$K(2)$
-localisations
![]() $\mathcal {E}^{\mathrm {top}}_{K(2)}$
and
$\mathcal {E}^{\mathrm {top}}_{K(2)}$
and
![]() $\mathcal {E}_{K(2)}$
are elliptic cohomology theories for
$\mathcal {E}_{K(2)}$
are elliptic cohomology theories for
![]() $R^{\mathrm {ss}}$
, and also split into products
$R^{\mathrm {ss}}$
, and also split into products
![]() $\mathcal {E}^{\mathrm {top}}_i$
and
$\mathcal {E}^{\mathrm {top}}_i$
and
![]() $\mathcal {E}_i$
in the homotopy category
$\mathcal {E}_i$
in the homotopy category
![]() $\mathrm {h}{\mathrm {CAlg}}_{K(2)}$
. It follows from [Reference Goerss, Hopkins and BakerGH04, Section 7] (also see [Reference LurieLur18, Remark 5.0.5] or [Reference Pstrkagowski and VanKoughnettPV19, Section 7]) that these
$\mathrm {h}{\mathrm {CAlg}}_{K(2)}$
. It follows from [Reference Goerss, Hopkins and BakerGH04, Section 7] (also see [Reference LurieLur18, Remark 5.0.5] or [Reference Pstrkagowski and VanKoughnettPV19, Section 7]) that these
![]() $K(2)$
-local
$K(2)$
-local
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\mathcal {E}_{K(2)}^{\mathrm {top}}$
and
$\mathcal {E}_{K(2)}^{\mathrm {top}}$
and
![]() $\mathcal {E}_{K(2)}$
are naturally equivalent to the product of Lubin–Tate
$\mathcal {E}_{K(2)}$
are naturally equivalent to the product of Lubin–Tate
![]() $\mathbf {E}_\infty $
-rings associated to the formal groups
$\mathbf {E}_\infty $
-rings associated to the formal groups
![]() $\widehat {E}^{\mathrm {ss}}_{\kappa _i}$
over the (finite and hence also) perfect fields
$\widehat {E}^{\mathrm {ss}}_{\kappa _i}$
over the (finite and hence also) perfect fields
![]() $\kappa _i$
. By idem, we see that morphisms between these Lubin–Tate
$\kappa _i$
. By idem, we see that morphisms between these Lubin–Tate
![]() $\mathbf {E}_\infty $
-rings are defined by the associated morphisms on the pairs
$\mathbf {E}_\infty $
-rings are defined by the associated morphisms on the pairs
![]() $(\kappa _i, \widehat {E}^{\mathrm {ss}}_{\kappa _i})$
. As
$(\kappa _i, \widehat {E}^{\mathrm {ss}}_{\kappa _i})$
. As
![]() $\mathrm {h}\phi _{K(2)}$
yields an equivalence on
$\mathrm {h}\phi _{K(2)}$
yields an equivalence on
![]() $\pi _0$
as well as an equivalence on associated Quillen formal groups, we see
$\pi _0$
as well as an equivalence on associated Quillen formal groups, we see
![]() $\mathrm {h}\phi _{K(2)}$
lifts to a morphism
$\mathrm {h}\phi _{K(2)}$
lifts to a morphism
![]() $\phi _{K(2)}\colon \mathcal {E}^{\mathrm {top}}_{K(2)}\to \mathcal {E}_{K(2)}$
of
$\phi _{K(2)}\colon \mathcal {E}^{\mathrm {top}}_{K(2)}\to \mathcal {E}_{K(2)}$
of
![]() $K(2)$
-local
$K(2)$
-local
![]() $\mathbf {E}_\infty $
-rings, which is unique up to contractible choice. This uniqueness allows us to use Proposition 3.1 to conclude that this collection of morphisms of
$\mathbf {E}_\infty $
-rings, which is unique up to contractible choice. This uniqueness allows us to use Proposition 3.1 to conclude that this collection of morphisms of
![]() $\mathbf {E}_\infty $
-rings define a natural morphism
$\mathbf {E}_\infty $
-rings define a natural morphism
![]() $\phi _{K(2)}\colon \mathscr {O}^{\mathrm {top}}_{K(2)}\to \mathscr {O}_{K(2)}$
of presheaves of
$\phi _{K(2)}\colon \mathscr {O}^{\mathrm {top}}_{K(2)}\to \mathscr {O}_{K(2)}$
of presheaves of
![]() $\mathbf {E}_\infty $
-rings on
$\mathbf {E}_\infty $
-rings on
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
 $K(1)$
-local case.
$K(1)$
-local case.
Consider the
![]() $K(1)$
-localisation of the map
$K(1)$
-localisation of the map
![]() $\mathrm {h}\phi $
of homotopy commutative ring spectra
$\mathrm {h}\phi $
of homotopy commutative ring spectra
![]() $\mathrm {h}\phi _{K(1)}\colon \mathcal {E}^{\mathrm {top}} _{K(1)}:=\mathrm {h}\mathscr {O}^{\mathrm {top}} _{K(1)}(R)\to \mathrm {h}\mathscr {O}_{K(1)}(R)=:\mathcal {E}_{K(1)}$
. Recall from [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.6], that the p-adic K-theory of an
$\mathrm {h}\phi _{K(1)}\colon \mathcal {E}^{\mathrm {top}} _{K(1)}:=\mathrm {h}\mathscr {O}^{\mathrm {top}} _{K(1)}(R)\to \mathrm {h}\mathscr {O}_{K(1)}(R)=:\mathcal {E}_{K(1)}$
. Recall from [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.6], that the p-adic K-theory of an
![]() $\mathbf {E}_\infty $
-ring has the structure of a
$\mathbf {E}_\infty $
-ring has the structure of a
![]() $\theta $
-
$\theta $
-
![]() $\pi _\ast \operatorname {\mathrm {KU}}_p$
-algebra, functorially in maps of
$\pi _\ast \operatorname {\mathrm {KU}}_p$
-algebra, functorially in maps of
![]() $\mathbf {E}_\infty $
-rings. (Recall that for a spectrum X, one defines its p-adic K-theory as the homotopy groups of the localisation
$\mathbf {E}_\infty $
-rings. (Recall that for a spectrum X, one defines its p-adic K-theory as the homotopy groups of the localisation
![]() ${\mathrm {K}}_\ast ^\wedge X=\pi _\ast L_{K(1)}(X\otimes \operatorname {\mathrm {KU}}_p)$
.) Let us write
${\mathrm {K}}_\ast ^\wedge X=\pi _\ast L_{K(1)}(X\otimes \operatorname {\mathrm {KU}}_p)$
.) Let us write
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ord}}$
for the moduli of generalised elliptic curves over p-complete rings with ordinary reduction modulo p (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12(1.1)]), and
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ord}}$
for the moduli of generalised elliptic curves over p-complete rings with ordinary reduction modulo p (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12(1.1)]), and
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ord}}(p^\infty )$
for the moduli stack of generalised elliptic curves E over p-complete rings and level structure given by an isomorphism
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ord}}(p^\infty )$
for the moduli stack of generalised elliptic curves E over p-complete rings and level structure given by an isomorphism
![]() $\widehat {{\mathbf {G}}}_m\simeq \widehat {E}$
of formal groups.
$\widehat {{\mathbf {G}}}_m\simeq \widehat {E}$
of formal groups.
Let us work globally for a moment. Recall how the global sections of
![]() $\mathscr {O}^{\mathrm {top}} _{K(1)}$
, written as
$\mathscr {O}^{\mathrm {top}} _{K(1)}$
, written as
![]() $\operatorname {\mathrm {Tmf}}_{K(1)}$
, are constructed in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12]. For odd primes p, we define
$\operatorname {\mathrm {Tmf}}_{K(1)}$
, are constructed in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12]. For odd primes p, we define
![]() $\operatorname {\mathrm {Tmf}}_{K(1)}$
as the
$\operatorname {\mathrm {Tmf}}_{K(1)}$
as the
![]() $\mathbf {F}_p^\times $
-homotopy fixed points of
$\mathbf {F}_p^\times $
-homotopy fixed points of
![]() $\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}$
, where this
$\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}$
, where this
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-ring is such that its p-adic K-theory W is given by pulling back the span of formal stacks
$\mathbf {E}_\infty $
-ring is such that its p-adic K-theory W is given by pulling back the span of formal stacks
and
![]() $\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p)$
is the moduli of generalised elliptic curves E over p-complete rings with ordinary reduction modulo p and level structure given by an isomorphism
$\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p)$
is the moduli of generalised elliptic curves E over p-complete rings with ordinary reduction modulo p and level structure given by an isomorphism
![]() $\mu _{p}\simeq \widehat {E}[p]$
of finite group schemes—both of the stacks on the left and right above are affine by [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 5.2], and written as
$\mu _{p}\simeq \widehat {E}[p]$
of finite group schemes—both of the stacks on the left and right above are affine by [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 5.2], and written as
![]() $\operatorname {\mathrm {Spf}} V_1$
and
$\operatorname {\mathrm {Spf}} V_1$
and
![]() $\operatorname {\mathrm {Spf}} V^\wedge _\infty $
, respectively. The
$\operatorname {\mathrm {Spf}} V^\wedge _\infty $
, respectively. The
![]() $\mathbf {F}_p^\times $
-structure on
$\mathbf {F}_p^\times $
-structure on
![]() $\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}$
comes from the fact that W is an
$\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}$
comes from the fact that W is an
![]() $\mathbf {F}_p^\times $
-torsor over
$\mathbf {F}_p^\times $
-torsor over
![]() $V^\wedge _\infty $
. The Goerss–Hopkins obstruction theory used to realise
$V^\wedge _\infty $
. The Goerss–Hopkins obstruction theory used to realise
![]() $\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}$
as an
$\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}$
as an
![]() $\mathbf {F}_p^\times $
-equivariant
$\mathbf {F}_p^\times $
-equivariant
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-ring with p-adic K-theory W also implies that such an
$\mathbf {E}_\infty $
-ring with p-adic K-theory W also implies that such an
![]() $\mathbf {F}_p^\times $
-equivariant
$\mathbf {F}_p^\times $
-equivariant
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-ring is unique up to homotopy; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Theorem 7.1] for the obstruction theory and the proof of [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Theorem 7.7] for justification that this works
$\mathbf {E}_\infty $
-ring is unique up to homotopy; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Theorem 7.1] for the obstruction theory and the proof of [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Theorem 7.7] for justification that this works
![]() $\mathbf {F}_p^\times $
-equivariantly. Pulling back
$\mathbf {F}_p^\times $
-equivariantly. Pulling back
![]() $\mathscr {O}_{K(1)}$
to
$\mathscr {O}_{K(1)}$
to
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ord}}$
, we see that
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ord}}$
, we see that
![]() $\mathcal {F}(p):=\mathscr {O}_{K(1)}(\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p))$
defines an elliptic cohomology theory for
$\mathcal {F}(p):=\mathscr {O}_{K(1)}(\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p))$
defines an elliptic cohomology theory for
![]() $\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p)$
by assumption, and by [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 6.1] we see the p-adic K-theory of
$\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p)$
by assumption, and by [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 6.1] we see the p-adic K-theory of
![]() $\mathcal {F}(p)$
is isomorphic to W as
$\mathcal {F}(p)$
is isomorphic to W as
![]() $\mathbf {Z}_p^\times $
-equivariant
$\mathbf {Z}_p^\times $
-equivariant
![]() $\mathbf {Z}_p$
-algebras. To see that this isomorphism is indeed an isomorphism of
$\mathbf {Z}_p$
-algebras. To see that this isomorphism is indeed an isomorphism of
![]() $\mathbf {F}_p^\times $
-equivariant
$\mathbf {F}_p^\times $
-equivariant
![]() $\theta $
-algebras, we need to see that the algebraic p-adic Adams operation
$\theta $
-algebras, we need to see that the algebraic p-adic Adams operation
![]() $\psi ^p_{\mathrm {alg}}$
on W agrees with the topological p-adic Adams operation
$\psi ^p_{\mathrm {alg}}$
on W agrees with the topological p-adic Adams operation
![]() $\psi ^p_{\mathrm{top}} $
on the p-adic K-theory of
$\psi ^p_{\mathrm{top}} $
on the p-adic K-theory of
![]() $\mathcal {F}(p)$
. This is done in the proof of Lemma 5.1 after Equation (5-2), to be stated and proven in Section 5 below. The uniquess of
$\mathcal {F}(p)$
. This is done in the proof of Lemma 5.1 after Equation (5-2), to be stated and proven in Section 5 below. The uniquess of
![]() $\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}$
up to homotopy gives us an equivalence of
$\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}$
up to homotopy gives us an equivalence of
![]() $\mathbf {F}_p^\times $
-equivariant
$\mathbf {F}_p^\times $
-equivariant
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}\simeq \mathcal {F}(p)$
. Taking
$\operatorname {\mathrm {Tmf}}(p)^{\mathrm {ord}}\simeq \mathcal {F}(p)$
. Taking
![]() $\mathbf {F}_p^\times $
-homotopy fixed points gives us an equivalence of
$\mathbf {F}_p^\times $
-homotopy fixed points gives us an equivalence of
![]() $\mathbf {E}_\infty $
-rings between
$\mathbf {E}_\infty $
-rings between
![]() $\operatorname {\mathrm {Tmf}}_{K(1)}$
and the global section of
$\operatorname {\mathrm {Tmf}}_{K(1)}$
and the global section of
![]() $\mathscr {O}_{K(1)}$
(note that
$\mathscr {O}_{K(1)}$
(note that
![]() $\mathscr {O}$
is an étale sheaf as it defines natural elliptic cohomology theories, so there is a well-defined notion of global sections). We now obtain a
$\mathscr {O}$
is an étale sheaf as it defines natural elliptic cohomology theories, so there is a well-defined notion of global sections). We now obtain a
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebra structure on the sections of
$\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebra structure on the sections of
![]() $\mathscr {O}_{K(1)}$
.
$\mathscr {O}_{K(1)}$
.
Suppose now that
![]() $p=2$
. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 16], there are pushout diagrams of
$p=2$
. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 16], there are pushout diagrams of
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings

for specified elements
![]() $\zeta \in \pi _{-1}\mathbf {S}_{K(1)}$
and
$\zeta \in \pi _{-1}\mathbf {S}_{K(1)}$
and
![]() $\theta (f)-h(f)\in \pi _0 T_\zeta $
, where
$\theta (f)-h(f)\in \pi _0 T_\zeta $
, where
![]() $\mathbf {P}$
denotes the free
$\mathbf {P}$
denotes the free
![]() $\mathbf {E}_\infty $
-ring functor from
$\mathbf {E}_\infty $
-ring functor from
![]() ${\mathrm {Sp}}$
. It is shown in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 16] (after the proof of Remark 7.3) that all
${\mathrm {Sp}}$
. It is shown in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 16] (after the proof of Remark 7.3) that all
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-elliptic cohomology theories have
$\mathbf {E}_\infty $
-elliptic cohomology theories have
![]() $\theta (f)=h(f)$
in their homotopy groups. This, combined with the fact that
$\theta (f)=h(f)$
in their homotopy groups. This, combined with the fact that
![]() $\pi _{-1}$
of an elliptic cohomology theory vanishes, implies that
$\pi _{-1}$
of an elliptic cohomology theory vanishes, implies that
![]() $\mathscr {O}_{K(1)}$
naturally takes values in
$\mathscr {O}_{K(1)}$
naturally takes values in
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebras.
$\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebras.
We return to the local picture, equipped with the knowledge that
![]() $\mathscr {O}_{K(1)}$
takes values in
$\mathscr {O}_{K(1)}$
takes values in
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebras. For another object
$\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebras. For another object
![]() $\operatorname {\mathrm {Spec}} R'\to \mathcal {M}_{\mathrm {Ell}}$
inside
$\operatorname {\mathrm {Spec}} R'\to \mathcal {M}_{\mathrm {Ell}}$
inside
![]() $\mathcal {U}$
, consider the map induced by the p-adic K-theory functor
$\mathcal {U}$
, consider the map induced by the p-adic K-theory functor
where
![]() $\mathcal {E}_{K(1)}':=\mathscr {O}_{K(1)}(R')$
. As in the construction of
$\mathcal {E}_{K(1)}':=\mathscr {O}_{K(1)}(R')$
. As in the construction of
![]() $\mathscr {O}^{\mathrm {top}} _{K(1)}$
found in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12] before Proposition 7.16, the map of Equation (4-1) is an equivalence of spaces. Despite the fact that each
$\mathscr {O}^{\mathrm {top}} _{K(1)}$
found in [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12] before Proposition 7.16, the map of Equation (4-1) is an equivalence of spaces. Despite the fact that each
![]() $\mathrm {h}\phi _{K(1)}$
is currently just a morphism of homotopy commutative ring spectra, Lemma 5.1 will guarantee that its zeroth p-adic K-theory is a morphism of
$\mathrm {h}\phi _{K(1)}$
is currently just a morphism of homotopy commutative ring spectra, Lemma 5.1 will guarantee that its zeroth p-adic K-theory is a morphism of
![]() $\theta $
-algebras. Moreover, this induced map of p-adic K-theories will be a morphism of
$\theta $
-algebras. Moreover, this induced map of p-adic K-theories will be a morphism of
![]() $(V_\infty ^\wedge )_\ast $
-
$(V_\infty ^\wedge )_\ast $
-
![]() $\theta $
-algebras from the natural identifications of the preceeding paragraphs. As
$\theta $
-algebras from the natural identifications of the preceeding paragraphs. As
![]() $\mathbf {Z}$
-graded p-adic K-theory obtains a
$\mathbf {Z}$
-graded p-adic K-theory obtains a
![]() $\theta $
-algebra structure from that in degree zero, the p-adic K-theory of
$\theta $
-algebra structure from that in degree zero, the p-adic K-theory of
![]() $\mathrm {h}\phi _{K(1)}$
defines an element inside the codomain of Equation (4-1) when
$\mathrm {h}\phi _{K(1)}$
defines an element inside the codomain of Equation (4-1) when
![]() $R'=R$
. By Proposition 3.1, we can therefore lift
$R'=R$
. By Proposition 3.1, we can therefore lift
![]() $\mathrm {h}\phi _{K(1)}\colon \mathrm {h}\mathscr {O}^{\mathrm {top}} _{K(1)}\to \mathrm {h}\mathscr {O}_{K(1)}$
to a morphism
$\mathrm {h}\phi _{K(1)}\colon \mathrm {h}\mathscr {O}^{\mathrm {top}} _{K(1)}\to \mathrm {h}\mathscr {O}_{K(1)}$
to a morphism
![]() $\phi _{K(1)}\colon \mathscr {O}^{\mathrm {top}} _{K(1)}\to \mathscr {O}_{K(1)}$
of presheaves of (
$\phi _{K(1)}\colon \mathscr {O}^{\mathrm {top}} _{K(1)}\to \mathscr {O}_{K(1)}$
of presheaves of (
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebras, so in particular of)
$\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebras, so in particular of)
![]() $\mathbf {E}_\infty $
-rings on
$\mathbf {E}_\infty $
-rings on
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
 $K(0)$
-local case.
$K(0)$
-local case.
The Morava K-theory spectrum
![]() $K(0)$
is equivalent to
$K(0)$
is equivalent to
![]() $\mathbf {Q}$
, the Eilenberg–MacLane spectrum of the rational numbers. We can actually lift
$\mathbf {Q}$
, the Eilenberg–MacLane spectrum of the rational numbers. We can actually lift
![]() $\mathrm {h}\phi _{\mathbf {Q}}$
globally, meaning we are not working section-by-section. Consider post-composing the functors
$\mathrm {h}\phi _{\mathbf {Q}}$
globally, meaning we are not working section-by-section. Consider post-composing the functors
![]() $\mathscr {O}^{\mathrm {top}}$
and
$\mathscr {O}^{\mathrm {top}}$
and
![]() $\mathscr {O}$
with the localisation functor
$\mathscr {O}$
with the localisation functor
![]() ${\mathrm {CAlg}}\to {\mathrm {CAlg}}_{\mathbf {Q}}$
, and denote the resulting presheaves with the subscript
${\mathrm {CAlg}}\to {\mathrm {CAlg}}_{\mathbf {Q}}$
, and denote the resulting presheaves with the subscript
![]() $\mathbf {Q}$
. By construction (also see [Reference Hill and LawsonHL16, Proposition 4.47]), the functor
$\mathbf {Q}$
. By construction (also see [Reference Hill and LawsonHL16, Proposition 4.47]), the functor
![]() $\mathscr {O}^{\mathrm {top}}_{\mathbf {Q}}$
is formal and by [Reference MeierMei21, Proposition 4.8], the sheaf
$\mathscr {O}^{\mathrm {top}}_{\mathbf {Q}}$
is formal and by [Reference MeierMei21, Proposition 4.8], the sheaf
![]() $\mathscr {O}_{\mathbf {Q}}$
is also formal. This yields the following chain of equivalences lifting
$\mathscr {O}_{\mathbf {Q}}$
is also formal. This yields the following chain of equivalences lifting
![]() $\mathrm {h}\phi _{\mathbf {Q}}$
:
$\mathrm {h}\phi _{\mathbf {Q}}$
:
Transchromatic compatibility.
We now have morphisms fitting into the following not a priori commutative solid diagram of presheaves of p-complete
![]() $\mathbf {E}_\infty $
-rings on
$\mathbf {E}_\infty $
-rings on
![]() $\mathcal {U}$
:
$\mathcal {U}$
:

The right face commutes by the naturality of the unit of the
![]() $K(1)$
-localisation functor. We also claim that the lower face commutes. In other words, we claim that for each
$K(1)$
-localisation functor. We also claim that the lower face commutes. In other words, we claim that for each
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}$
inside
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}$
inside
![]() $\mathcal {U}$
, there is a natural path
$\mathcal {U}$
, there is a natural path
![]() $\gamma (R)$
between
$\gamma (R)$
between
![]() $\alpha _{\mathrm {chrom}}\circ \phi _{K(1)}$
and
$\alpha _{\mathrm {chrom}}\circ \phi _{K(1)}$
and
![]() $(\phi _{K(2)})_{K(1)}\circ \alpha _{\mathrm {chrom}}^{\mathrm {top}}$
as maps of
$(\phi _{K(2)})_{K(1)}\circ \alpha _{\mathrm {chrom}}^{\mathrm {top}}$
as maps of
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\operatorname {\mathrm {Tmf}}$
-algebras. Note that the
$\operatorname {\mathrm {Tmf}}$
-algebras. Note that the
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\operatorname {\mathrm {Tmf}}$
-algebra structure on
$\operatorname {\mathrm {Tmf}}$
-algebra structure on
![]() $(\mathscr {O}_{K(2)})_{K(1)}$
can come from either one of these maps (and a posteriori, these two choices will agree up to homotopy). As we see from the discussion following [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 8.8], the p-adic K-theory functor induces an equivalence
$(\mathscr {O}_{K(2)})_{K(1)}$
can come from either one of these maps (and a posteriori, these two choices will agree up to homotopy). As we see from the discussion following [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 8.8], the p-adic K-theory functor induces an equivalence
where
![]() $(V_\infty ^\wedge )_\ast $
denotes the p-adic K-theory of
$(V_\infty ^\wedge )_\ast $
denotes the p-adic K-theory of
![]() $\operatorname {\mathrm {Tmf}}$
; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.5] and [Reference Behrens and MillerBeh20, Section 6]. As
$\operatorname {\mathrm {Tmf}}$
; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.5] and [Reference Behrens and MillerBeh20, Section 6]. As
![]() $\alpha _{\mathrm {chrom}}\circ \phi _{K(1)}$
and
$\alpha _{\mathrm {chrom}}\circ \phi _{K(1)}$
and
![]() $(\phi _{K(2)})_{K(1)}\circ \alpha _{\mathrm {chrom}}^{\mathrm {top}}$
are isomorphic as functors into
$(\phi _{K(2)})_{K(1)}\circ \alpha _{\mathrm {chrom}}^{\mathrm {top}}$
are isomorphic as functors into
![]() ${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
and hence also in the codomain of Equation (4-3), we see these morphisms are homotopic as morphisms of
${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
and hence also in the codomain of Equation (4-3), we see these morphisms are homotopic as morphisms of
![]() $\mathbf {E}_\infty $
-rings by the above equivalence. From the equivalence in Equation (4-3), we can employ Proposition 3.1 to obtain a homotopy between
$\mathbf {E}_\infty $
-rings by the above equivalence. From the equivalence in Equation (4-3), we can employ Proposition 3.1 to obtain a homotopy between
![]() $\alpha _{\mathrm {chrom}}\circ \phi _{K(1)}$
and
$\alpha _{\mathrm {chrom}}\circ \phi _{K(1)}$
and
![]() $(\phi _{K(2)})_{K(1)}\circ \alpha _{\mathrm {chrom}}^{\mathrm {top}}$
as morphisms of presheaves of
$(\phi _{K(2)})_{K(1)}\circ \alpha _{\mathrm {chrom}}^{\mathrm {top}}$
as morphisms of presheaves of
![]() $K(1)$
-local
$K(1)$
-local
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebras from
$\operatorname {\mathrm {Tmf}}_{K(1)}$
-algebras from
![]() $\mathscr {O}^{\mathrm {top}}_{K(1)}$
to
$\mathscr {O}^{\mathrm {top}}_{K(1)}$
to
![]() $(\mathscr {O}_{K(2)})_{K(1)}$
. Using the fact that the front and back faces of Equation (4-2) are Cartesian, we obtain a natural morphism of presheaves of p-complete
$(\mathscr {O}_{K(2)})_{K(1)}$
. Using the fact that the front and back faces of Equation (4-2) are Cartesian, we obtain a natural morphism of presheaves of p-complete
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\phi _p\colon \mathscr {O}_p^{\mathrm {top}}\to \mathscr {O}_p$
on
$\phi _p\colon \mathscr {O}_p^{\mathrm {top}}\to \mathscr {O}_p$
on
![]() $\mathcal {U}$
which agrees with
$\mathcal {U}$
which agrees with
![]() $\mathrm {h}\phi _p$
inside the category of presheaves functors from
$\mathrm {h}\phi _p$
inside the category of presheaves functors from
![]() $\mathcal {U}$
to
$\mathcal {U}$
to
![]() ${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
, as indicated by the dashed morphism in Equation (4-2).
${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
, as indicated by the dashed morphism in Equation (4-2).
Arithmetic compatibility.
Currently, we have morphisms
![]() $\phi _{\mathbf {Q}}$
and
$\phi _{\mathbf {Q}}$
and
![]() $\phi _p$
fitting into the not a priori commutative solid diagram of presheaves of
$\phi _p$
fitting into the not a priori commutative solid diagram of presheaves of
![]() $\mathbf {E}_\infty $
-rings on
$\mathbf {E}_\infty $
-rings on
![]() $\mathcal {U}$
:
$\mathcal {U}$
:

Similar to the transchromatic compatibilities, the right face naturally commutes, so we are left to argue why the lower face commutes. To study the lower face, let us first work on the open substacks
![]() $\mathcal {M}_{\mathrm {Ell}}[c_4^{-1}]$
and
$\mathcal {M}_{\mathrm {Ell}}[c_4^{-1}]$
and
![]() $\mathcal {M}_{\mathrm {Ell}}[\Delta ^{-1}]$
of
$\mathcal {M}_{\mathrm {Ell}}[\Delta ^{-1}]$
of
![]() $\mathcal {M}_{\mathrm {Ell}}$
, which themselves form a cover of
$\mathcal {M}_{\mathrm {Ell}}$
, which themselves form a cover of
![]() $\mathcal {M}_{\mathrm {Ell}}$
; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.9]. We then follow an analogous argument to the transchromatic situation above; see the discussion following [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 9.4] which shows the discreteness of the desired mapping spaces. Indeed, as the two homotopies witnessing the commutativity of the lower face of Equation (4-4) restricted to the substacks
$\mathcal {M}_{\mathrm {Ell}}$
; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.9]. We then follow an analogous argument to the transchromatic situation above; see the discussion following [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 9.4] which shows the discreteness of the desired mapping spaces. Indeed, as the two homotopies witnessing the commutativity of the lower face of Equation (4-4) restricted to the substacks
![]() $\mathcal {M}_{\mathrm {Ell}}[c_4^{-1}]$
and
$\mathcal {M}_{\mathrm {Ell}}[c_4^{-1}]$
and
![]() $\mathcal {M}_{\mathrm {Ell}}[\Delta ^{-1}]$
agree on their intersection
$\mathcal {M}_{\mathrm {Ell}}[\Delta ^{-1}]$
agree on their intersection
![]() $\mathcal {M}_{\mathrm {Ell}}[c_4^{-1},\Delta ^{-1}]$
(as the mapping spaces in question are discrete), these homotopies then glue to a homotopy on
$\mathcal {M}_{\mathrm {Ell}}[c_4^{-1},\Delta ^{-1}]$
(as the mapping spaces in question are discrete), these homotopies then glue to a homotopy on
![]() $\mathcal {M}_{\mathrm {Ell}}$
. This yields a homotopy witnessing the commutativity of the lower face of Equation (4-4). As the front and back faces of Equation (4-4) are Cartesian, we obtain our final natural equivalence of presheaves of
$\mathcal {M}_{\mathrm {Ell}}$
. This yields a homotopy witnessing the commutativity of the lower face of Equation (4-4). As the front and back faces of Equation (4-4) are Cartesian, we obtain our final natural equivalence of presheaves of
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\phi \colon \mathcal {E}^{\mathrm {top}}\to \mathcal {E}$
on
$\phi \colon \mathcal {E}^{\mathrm {top}}\to \mathcal {E}$
on
![]() $\mathcal {U}$
, lifting
$\mathcal {U}$
, lifting
![]() $\mathrm {h}\phi $
.
$\mathrm {h}\phi $
.
Therefore,
![]() $\mathcal {Z}$
is connected. The same argument can be made for
$\mathcal {Z}$
is connected. The same argument can be made for
![]() $\mathcal {Z}^{\mathrm {sm}}$
; see Remark 5.6 for why Lemma 5.1 simplifies in this case.
$\mathcal {Z}^{\mathrm {sm}}$
; see Remark 5.6 for why Lemma 5.1 simplifies in this case.
5 Compatibility of
 $\theta $
-algebra structures
$\theta $
-algebra structures
The above proof of Theorem 2.1 is contingent on Lemma 5.1 below, whose proof we find rather delicate. Recall from [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.6] that the p-adic K-theory of an
![]() $\mathbf {E}_\infty $
-ring has the structure of a
$\mathbf {E}_\infty $
-ring has the structure of a
![]() $\theta $
-algebra, and this structure is functorial in morphisms of
$\theta $
-algebra, and this structure is functorial in morphisms of
![]() $\mathbf {E}_\infty $
-rings.
$\mathbf {E}_\infty $
-rings.
Lemma 5.1. Fix a prime p. Let
![]() $\mathscr {O}$
be an object of
$\mathscr {O}$
be an object of
![]() $\mathcal {Z}$
and
$\mathcal {Z}$
and
![]() $\mathrm {h}\phi \colon \mathrm {h}\mathscr {O}^{\mathrm {top}}\xrightarrow {\simeq }\mathrm {h}\mathscr {O}$
be the given equivalence of diagrams of homotopy commutative ring spectra. Then for any étale
$\mathrm {h}\phi \colon \mathrm {h}\mathscr {O}^{\mathrm {top}}\xrightarrow {\simeq }\mathrm {h}\mathscr {O}$
be the given equivalence of diagrams of homotopy commutative ring spectra. Then for any étale
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
, the map induced by
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
, the map induced by
on the zeroth p-adic K-theory ring is a morphism of
![]() $\theta $
-algebras.
$\theta $
-algebras.
In general, it is not true that a morphism of homotopy commutative ring spectra should induce a morphism of
![]() $\theta $
-algebras upon taking their p-adic K-theory, even if the homotopy commutative ring spectra involved come equipped with some
$\theta $
-algebras upon taking their p-adic K-theory, even if the homotopy commutative ring spectra involved come equipped with some
![]() $\mathbf {E}_\infty $
-structures.
$\mathbf {E}_\infty $
-structures.
However, in the situation above, the sections of the
![]() $K(2)$
-localisation of the sheaf of
$K(2)$
-localisation of the sheaf of
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\mathscr {O}$
have a prescribed
$\mathscr {O}$
have a prescribed
![]() $\mathbf {E}_\infty $
-structure given by Lubin–Tate spectra (also called Morava E-theories); see the
$\mathbf {E}_\infty $
-structure given by Lubin–Tate spectra (also called Morava E-theories); see the
![]() $K(2)$
-local case in the proof of Theorem 2.1 above. In particular, this means that an equivalence of homotopy commutative ring spectra
$K(2)$
-local case in the proof of Theorem 2.1 above. In particular, this means that an equivalence of homotopy commutative ring spectra
![]() $\mathcal {F}^{\mathrm {top}}_{K(2)}\simeq \mathcal {F}_{K(2)}$
can be refined to an equivalence of
$\mathcal {F}^{\mathrm {top}}_{K(2)}\simeq \mathcal {F}_{K(2)}$
can be refined to an equivalence of
![]() $\mathbf {E}_\infty $
-rings, as both objects are naturally Lubin–Tate spectra. It follows that the
$\mathbf {E}_\infty $
-rings, as both objects are naturally Lubin–Tate spectra. It follows that the
![]() $K(1)$
-localisation of this equivalence of
$K(1)$
-localisation of this equivalence of
![]() $\mathbf {E}_\infty $
-rings induces a morphism of
$\mathbf {E}_\infty $
-rings induces a morphism of
![]() $\theta $
-algebras on p-adic K-theory. The comparison map in the chromatic fracture square between the
$\theta $
-algebras on p-adic K-theory. The comparison map in the chromatic fracture square between the
![]() $K(1)$
-localisation of
$K(1)$
-localisation of
![]() $\mathscr {O}$
and the
$\mathscr {O}$
and the
![]() $K(1)$
-localisation of its
$K(1)$
-localisation of its
![]() $K(2)$
-localisation is also a map of
$K(2)$
-localisation is also a map of
![]() $\mathbf {E}_\infty $
-rings. If we can show this map induces an injection on p-adic K-theory, then it would be clear that the equivalence of homotopy commutative ring spectra
$\mathbf {E}_\infty $
-rings. If we can show this map induces an injection on p-adic K-theory, then it would be clear that the equivalence of homotopy commutative ring spectra
![]() $\mathcal {F}^{\mathrm {top}}_{K(1)}\simeq \mathcal {F}_{K(1)}$
induces a morphism of
$\mathcal {F}^{\mathrm {top}}_{K(1)}\simeq \mathcal {F}_{K(1)}$
induces a morphism of
![]() $\theta $
-algebras on p-adic K-theory, which would lead us to Lemma 5.1.
$\theta $
-algebras on p-adic K-theory, which would lead us to Lemma 5.1.
This is first done for an explicit étale morphism into
![]() $\mathcal {M}_{\mathrm {Ell}}$
, which has the properties that it covers
$\mathcal {M}_{\mathrm {Ell}}$
, which has the properties that it covers
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
and each of its connected components is an integral domain. Some descent and deformation theory is then used to obtain this result for a general étale morphism.
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
and each of its connected components is an integral domain. Some descent and deformation theory is then used to obtain this result for a general étale morphism.
Proof. To show
![]() $\lambda : \mathrm {K}^\wedge _0 \mathcal {F}^{\mathrm {top}}\to \mathrm {K}^\wedge _0 \mathcal {F}$
, the map induced by
$\lambda : \mathrm {K}^\wedge _0 \mathcal {F}^{\mathrm {top}}\to \mathrm {K}^\wedge _0 \mathcal {F}$
, the map induced by
![]() $\mathrm {h}\phi $
on p-adic K-theory, is a morphism of
$\mathrm {h}\phi $
on p-adic K-theory, is a morphism of
![]() $\theta $
-algebras, one must check it commutes with the stable p-adic Adams operations
$\theta $
-algebras, one must check it commutes with the stable p-adic Adams operations
![]() $\psi ^\ell $
for every
$\psi ^\ell $
for every
![]() $\ell \in \mathbf {Z}_p^\times $
as well as the action of the operator
$\ell \in \mathbf {Z}_p^\times $
as well as the action of the operator
![]() $\theta $
. The stable p-adic Adams operations
$\theta $
. The stable p-adic Adams operations
![]() $\psi ^\ell $
are constructed on the spectrum
$\psi ^\ell $
are constructed on the spectrum
![]() $\operatorname {\mathrm {KU}}_p$
, so we automatically have compatibility with them for any map of spectra. It is shown shortly that both rings above are étale over the ring
$\operatorname {\mathrm {KU}}_p$
, so we automatically have compatibility with them for any map of spectra. It is shown shortly that both rings above are étale over the ring
![]() $V^\wedge _\infty $
, and hence they are
$V^\wedge _\infty $
, and hence they are
![]() $V^\wedge _\infty $
-torsion free, where we remind the reader that
$V^\wedge _\infty $
-torsion free, where we remind the reader that
![]() $V^\wedge _\infty $
is the ring of generalised p-adic modular forms discussed after the proof of [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 5.2] or in the
$V^\wedge _\infty $
is the ring of generalised p-adic modular forms discussed after the proof of [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 5.2] or in the
![]() $K(1)$
-local discussions of [Reference Behrens and MillerBeh20]. In particular, this implies that both
$K(1)$
-local discussions of [Reference Behrens and MillerBeh20]. In particular, this implies that both
![]() $\mathrm {K}^\wedge _0\mathcal {F}^{\mathrm {top}}$
and
$\mathrm {K}^\wedge _0\mathcal {F}^{\mathrm {top}}$
and
![]() $\mathrm {K}^\wedge _0\mathcal {F}$
are
$\mathrm {K}^\wedge _0\mathcal {F}$
are
![]() $\mathbf {Z}_p$
-torsion free, in which case the operator
$\mathbf {Z}_p$
-torsion free, in which case the operator
![]() $\theta $
is an equivalent datum to the p-adic Adams operator
$\theta $
is an equivalent datum to the p-adic Adams operator
![]() $\psi ^p$
; see [Reference Goerss, Hopkins and BakerGH04, Remark 2.2.5]. It therefore suffices to show that the following diagram of
$\psi ^p$
; see [Reference Goerss, Hopkins and BakerGH04, Remark 2.2.5]. It therefore suffices to show that the following diagram of
![]() $\mathbf {Z}_p$
-algebras commutes:
$\mathbf {Z}_p$
-algebras commutes:

Let us write
![]() $R^{\mathrm {ord}}$
for the base-change of
$R^{\mathrm {ord}}$
for the base-change of
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
over
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
over
![]() $\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}\to \widehat {\mathcal {M}}_{\mathrm {Ell}}\to \mathcal {M}_{\mathrm {Ell}}$
, where
$\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}\to \widehat {\mathcal {M}}_{\mathrm {Ell}}\to \mathcal {M}_{\mathrm {Ell}}$
, where
![]() $\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
is the moduli stack of generalised elliptic curves over p-complete rings whose reduction modulo p is ordinary. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 7.16], we see
$\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
is the moduli stack of generalised elliptic curves over p-complete rings whose reduction modulo p is ordinary. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 7.16], we see
![]() $\mathcal {F}^{\mathrm {top}}_{K(1)}$
is an elliptic cohomology theory for
$\mathcal {F}^{\mathrm {top}}_{K(1)}$
is an elliptic cohomology theory for
![]() $\operatorname {\mathrm {Spf}} R^{\mathrm {ord}}\to \mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
, and we can also consider
$\operatorname {\mathrm {Spf}} R^{\mathrm {ord}}\to \mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
, and we can also consider
![]() $\mathcal {F}_{K(1)}$
as an elliptic cohomology theory using
$\mathcal {F}_{K(1)}$
as an elliptic cohomology theory using
![]() $\mathrm {h}\phi _{K(1)}$
. Define W using the Cartesian diagram of formal stacks
$\mathrm {h}\phi _{K(1)}$
. Define W using the Cartesian diagram of formal stacks

where
![]() $\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p^\infty )$
is the formal stack of generalised elliptic curves E with ordinary reduction modulo p with a given isomorphism of formal groups
$\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p^\infty )$
is the formal stack of generalised elliptic curves E with ordinary reduction modulo p with a given isomorphism of formal groups
![]() $\eta \colon \widehat {\mathbf {G}}_m\to \widehat {E}$
; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.5]. The stack
$\eta \colon \widehat {\mathbf {G}}_m\to \widehat {E}$
; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.5]. The stack
![]() $\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p^\infty )$
is represented by the formal affine scheme
$\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p^\infty )$
is represented by the formal affine scheme
![]() $\operatorname {\mathrm {Spf}} V_\infty ^\wedge $
which is ind-étale over
$\operatorname {\mathrm {Spf}} V_\infty ^\wedge $
which is ind-étale over
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ord}}$
; see the discussion after the proof of [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 5.2]. This W also has the structure of a
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {ord}}$
; see the discussion after the proof of [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 5.2]. This W also has the structure of a
![]() $\theta $
-algebra (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.6]), and we denote the p-adic Adams operation on W by
$\theta $
-algebra (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12.6]), and we denote the p-adic Adams operation on W by
![]() $\psi ^p_{\mathrm {alg}}$
. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 6.1], or rather its proof, we obtain isomorphisms of
$\psi ^p_{\mathrm {alg}}$
. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 6.1], or rather its proof, we obtain isomorphisms of
![]() $\mathbf {Z}_p$
-algebras
$\mathbf {Z}_p$
-algebras
![]() $v^{\mathrm {top}}\colon \mathrm {K}^\wedge _0 \mathcal {F}^{\mathrm {top}}\simeq W$
and
$v^{\mathrm {top}}\colon \mathrm {K}^\wedge _0 \mathcal {F}^{\mathrm {top}}\simeq W$
and
![]() $v\colon \mathrm {K}^\wedge _0 \mathcal {F}\simeq W$
, which are natural in complex orientation-preserving morphisms in
$v\colon \mathrm {K}^\wedge _0 \mathcal {F}\simeq W$
, which are natural in complex orientation-preserving morphisms in
![]() ${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
. These isomorphisms are not a priori isomorphisms of
${\mathrm {CAlg}}(\mathrm {h}\mathrm {Sp})$
. These isomorphisms are not a priori isomorphisms of
![]() $\theta $
-algebras; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Definition 6.2]. As
$\theta $
-algebras; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Definition 6.2]. As
![]() $\mathcal {F}$
obtains the structure of an elliptic cohomology theory for
$\mathcal {F}$
obtains the structure of an elliptic cohomology theory for
![]() $R^{\mathrm {ord}}$
from the equivalence
$R^{\mathrm {ord}}$
from the equivalence
![]() $\mathrm {h}\phi _{K(1)}$
, we see that the following diagram of isomorphisms of
$\mathrm {h}\phi _{K(1)}$
, we see that the following diagram of isomorphisms of
![]() $\mathbf {Z}_p$
-algebras commutes:
$\mathbf {Z}_p$
-algebras commutes:

By construction (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 6.3]), we see
![]() $v^{\mathrm {top}}$
is an isomorphism of
$v^{\mathrm {top}}$
is an isomorphism of
![]() $\theta $
-algebras. To show
$\theta $
-algebras. To show
![]() $\lambda $
is a morphism of
$\lambda $
is a morphism of
![]() $\theta $
-algebras, it suffices to show v is a morphism of
$\theta $
-algebras, it suffices to show v is a morphism of
![]() $\theta $
-algebras, or in other words, Equation (5-1) commutes if and only if the following diagram of
$\theta $
-algebras, or in other words, Equation (5-1) commutes if and only if the following diagram of
![]() $\mathbf {Z}_p$
-algebras commutes:
$\mathbf {Z}_p$
-algebras commutes:

Let us now prove this is the case for a specific étale map
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
.
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
.
Choosing a particular étale morphism. Recall the moduli stack
![]() $\mathcal {M}^{\mathrm {sm}}_1(N)$
of smooth elliptic curves with
$\mathcal {M}^{\mathrm {sm}}_1(N)$
of smooth elliptic curves with
![]() $\Gamma _1(N)$
-level structure. These objects are discussed at length in [Reference Deligne, Rapoport, Deligne and KuykDR73, Section IV.3] and [Reference Katz and MazurKM85], and summaries for homotopy theorists can be found in [Reference Behrens and MillerBeh20, (6.3.8)] or [Reference MeierMei22, Section 2.1], for example. Importantly, recall the map
$\Gamma _1(N)$
-level structure. These objects are discussed at length in [Reference Deligne, Rapoport, Deligne and KuykDR73, Section IV.3] and [Reference Katz and MazurKM85], and summaries for homotopy theorists can be found in [Reference Behrens and MillerBeh20, (6.3.8)] or [Reference MeierMei22, Section 2.1], for example. Importantly, recall the map
![]() $\mathcal {M}^{\mathrm {sm}}_1(N)\to \mathcal {M}_{\mathrm {Ell}, \mathbf {Z}[{1}/{N}]}^{\mathrm {sm}}$
is an étale cover and that for
$\mathcal {M}^{\mathrm {sm}}_1(N)\to \mathcal {M}_{\mathrm {Ell}, \mathbf {Z}[{1}/{N}]}^{\mathrm {sm}}$
is an étale cover and that for
![]() $N\geq 4$
, the moduli stack
$N\geq 4$
, the moduli stack
![]() $\mathcal {M}^{\mathrm {sm}}_1(N)$
is in fact affine. This implies that the morphism of stacks
$\mathcal {M}^{\mathrm {sm}}_1(N)$
is in fact affine. This implies that the morphism of stacks
is étale, and the restriction to
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
is an étale cover. By base-change over
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
is an étale cover. By base-change over
![]() $\operatorname {\mathrm {Spf}} \mathbf {Z}_p$
, we obtain an étale map
$\operatorname {\mathrm {Spf}} \mathbf {Z}_p$
, we obtain an étale map
![]() $E: \operatorname {\mathrm {Spf}} \widehat {A}\to \widehat {\mathcal {M}}_{\mathrm {Ell}}$
. Following [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 8.7], write
$E: \operatorname {\mathrm {Spf}} \widehat {A}\to \widehat {\mathcal {M}}_{\mathrm {Ell}}$
. Following [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 8.7], write
![]() $A_\ast $
for the graded ring defined by
$A_\ast $
for the graded ring defined by
![]() $A_{2k}=\omega ^{\otimes k}_E(\operatorname {\mathrm {Spf}} \widehat {A})$
where E is the elliptic curve over
$A_{2k}=\omega ^{\otimes k}_E(\operatorname {\mathrm {Spf}} \widehat {A})$
where E is the elliptic curve over
![]() $\widehat {A}$
defined by the map of formal stacks above. Note that the Hasse invariant
$\widehat {A}$
defined by the map of formal stacks above. Note that the Hasse invariant
![]() $v_1$
for E lives in
$v_1$
for E lives in
![]() $A_{2(p-1)}$
. Let us also make the following definitions:
$A_{2(p-1)}$
. Let us also make the following definitions:
If we omit the subscript
![]() $\ast $
, we are implicitly considering the ring in degree zero. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 (8.6)], there is a canonical map
$\ast $
, we are implicitly considering the ring in degree zero. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 (8.6)], there is a canonical map
![]() $\alpha _\ast \colon A_\ast ^{\mathrm {ord}}\to (A_\ast ^{\mathrm {ss}})^{\mathrm {ord}}$
as
$\alpha _\ast \colon A_\ast ^{\mathrm {ord}}\to (A_\ast ^{\mathrm {ss}})^{\mathrm {ord}}$
as
![]() $v_1$
is invertible in
$v_1$
is invertible in
![]() $(A_\ast ^{\mathrm {ss}})^{\mathrm {ord}}$
, and we now define
$(A_\ast ^{\mathrm {ss}})^{\mathrm {ord}}$
, and we now define
![]() $W^{\mathrm {ss}}$
using the diagram of stacks
$W^{\mathrm {ss}}$
using the diagram of stacks

where all squares are Cartesian. The ring
![]() $W^{\mathrm {ss}}$
obtains a
$W^{\mathrm {ss}}$
obtains a
![]() $\theta $
-algebra structure from the above diagram, and in such a way that
$\theta $
-algebra structure from the above diagram, and in such a way that
![]() $\widetilde {\alpha }\colon W\to W^{\mathrm {ss}}$
is a morphism of
$\widetilde {\alpha }\colon W\to W^{\mathrm {ss}}$
is a morphism of
![]() $\theta $
-algebras; see the discussion after the proof of [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 8.6]. We claim that
$\theta $
-algebras; see the discussion after the proof of [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 8.6]. We claim that
![]() $\widetilde {\alpha }$
comes from a map of
$\widetilde {\alpha }$
comes from a map of
![]() $\mathbf {E}_\infty $
-rings.
$\mathbf {E}_\infty $
-rings.
Claim 5.2. The zeroth p-adic K-theory of the canonical map of
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
is isomorphic to
![]() $\widetilde {\alpha }$
.
$\widetilde {\alpha }$
.
Proof of Claim 5.2. Specialising from the case of
![]() $\mathcal {F}_{K(1)}$
discussed above, we see that
$\mathcal {F}_{K(1)}$
discussed above, we see that
![]() $\mathcal {F}^{\mathrm {ord}}$
is an elliptic cohomology theory for the map
$\mathcal {F}^{\mathrm {ord}}$
is an elliptic cohomology theory for the map
![]() $\operatorname {\mathrm {Spf}} A^{\mathrm {ord}}\to \mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
, and similarly by [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 8.8], we see that
$\operatorname {\mathrm {Spf}} A^{\mathrm {ord}}\to \mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
, and similarly by [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 8.8], we see that
![]() $(\mathcal {F}^{\mathrm {ss}})^{\mathrm {ord}}$
is an elliptic cohomology theory for the map
$(\mathcal {F}^{\mathrm {ss}})^{\mathrm {ord}}$
is an elliptic cohomology theory for the map
![]() $\operatorname {\mathrm {Spf}} (A^{\mathrm {ss}})^{\mathrm {ord}}\to \mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
. The same is true for
$\operatorname {\mathrm {Spf}} (A^{\mathrm {ss}})^{\mathrm {ord}}\to \mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
. The same is true for
![]() $\mathcal {A}=\mathscr {O}^{\mathrm {top}}_{K(1)}(A)$
and
$\mathcal {A}=\mathscr {O}^{\mathrm {top}}_{K(1)}(A)$
and
![]() $(\mathscr {O}^{\mathrm {top}}_{K(2)}(A))_{K(1)}=\mathcal {A}'$
, and in this case, we know that taking
$(\mathscr {O}^{\mathrm {top}}_{K(2)}(A))_{K(1)}=\mathcal {A}'$
, and in this case, we know that taking
![]() $\pi _0$
of
$\pi _0$
of
![]() $\alpha _{\mathrm {chrom}}^{\mathrm {top}}\colon \mathcal {A}\to \mathcal {A}'$
is isomorphic to
$\alpha _{\mathrm {chrom}}^{\mathrm {top}}\colon \mathcal {A}\to \mathcal {A}'$
is isomorphic to
![]() $\alpha \colon A^{\mathrm {ord}}\to (A^{\mathrm {ss}})^{\mathrm {ord}}$
by construction; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 8.7]. The naturality of
$\alpha \colon A^{\mathrm {ord}}\to (A^{\mathrm {ss}})^{\mathrm {ord}}$
by construction; see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 8.7]. The naturality of
![]() $\mathrm {h}\phi \colon \mathscr {O}^{\mathrm {top}}\to \mathscr {O}$
and the chromatic fracture square imply that
$\mathrm {h}\phi \colon \mathscr {O}^{\mathrm {top}}\to \mathscr {O}$
and the chromatic fracture square imply that
![]() $\pi _0$
of the natural map of
$\pi _0$
of the natural map of
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\alpha _{\mathrm {chrom}}\colon \mathcal {F}^{\mathrm {ord}}\to (\mathcal {F}^{\mathrm {ss}})^{\mathrm {ord}}$
also realises
$\alpha _{\mathrm {chrom}}\colon \mathcal {F}^{\mathrm {ord}}\to (\mathcal {F}^{\mathrm {ss}})^{\mathrm {ord}}$
also realises
![]() $\alpha $
, and hence taking zeroth p-adic K-theory realises
$\alpha $
, and hence taking zeroth p-adic K-theory realises
![]() $\widetilde {\alpha }$
. This proves Claim 5.2.
$\widetilde {\alpha }$
. This proves Claim 5.2.
Recall that
![]() $\mathcal {F}^{\mathrm {ord}}=\mathscr {O}_{K(1)}(A)$
for our choice of A above. Consider the diagram of
$\mathcal {F}^{\mathrm {ord}}=\mathscr {O}_{K(1)}(A)$
for our choice of A above. Consider the diagram of
![]() $\mathbf {Z}_p$
-algebras
$\mathbf {Z}_p$
-algebras

where the maps are the obvious ones used above, and all the vertical morphisms are the unstable Adams operations:
![]() $\psi ^p_{\mathrm {top}}$
on the left and
$\psi ^p_{\mathrm {top}}$
on the left and
![]() $\psi ^p_{\mathrm {alg}}$
on the right. Note that the upper and lower faces commute by Claim 5.2, the right face commutes as
$\psi ^p_{\mathrm {alg}}$
on the right. Note that the upper and lower faces commute by Claim 5.2, the right face commutes as
![]() $\widetilde {\alpha }\colon W\to W^{\mathrm {ss}}$
is a morphism of
$\widetilde {\alpha }\colon W\to W^{\mathrm {ss}}$
is a morphism of
![]() $\theta $
-algebras and the left face commutes as
$\theta $
-algebras and the left face commutes as
![]() $\alpha _{\mathrm {chrom}}$
is a morphism of
$\alpha _{\mathrm {chrom}}$
is a morphism of
![]() $\mathbf {E}_\infty $
-rings. Most importantly, the front face also commutes. Indeed, from the arguments in the
$\mathbf {E}_\infty $
-rings. Most importantly, the front face also commutes. Indeed, from the arguments in the
![]() $K(2)$
-local case of the proof of Theorem 2.1, we see
$K(2)$
-local case of the proof of Theorem 2.1, we see
![]() $\mathcal {F}^{\mathrm {ss}}$
is naturally equivalent to a product of
$\mathcal {F}^{\mathrm {ss}}$
is naturally equivalent to a product of
![]() $K(2)$
-local Lubin–Tate spectra recognising the given elliptic curve over
$K(2)$
-local Lubin–Tate spectra recognising the given elliptic curve over
![]() $\operatorname {\mathrm {Spf}} A^{\mathrm {ss}}$
, and we can then apply [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Theorem 6.10]; the hypotheses and proof of this theorem are dispersed between pages 21 and 24 of idem. The back face of Equation (5-3) is precisely Equation (5-2) for
$\operatorname {\mathrm {Spf}} A^{\mathrm {ss}}$
, and we can then apply [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Theorem 6.10]; the hypotheses and proof of this theorem are dispersed between pages 21 and 24 of idem. The back face of Equation (5-3) is precisely Equation (5-2) for
![]() $R=A$
.
$R=A$
.
Claim 5.3. The morphism
![]() $\widetilde {\alpha }\colon W\to W^{\mathrm {ss}}$
is injective.
$\widetilde {\alpha }\colon W\to W^{\mathrm {ss}}$
is injective.
Using this claim for now, to show that the back face of Equation (5-3) commutes, it suffices to do so after post-composing with
![]() $\widetilde {\alpha }$
. This follows from the above considerations by a diagram chase. Hence, the back face of Equation (5-3) commutes, which yields the commutativity of Equation (5-2) for this particular choice of étale map
$\widetilde {\alpha }$
. This follows from the above considerations by a diagram chase. Hence, the back face of Equation (5-3) commutes, which yields the commutativity of Equation (5-2) for this particular choice of étale map
![]() $\operatorname {\mathrm {Spec}} A\to \mathcal {M}_{\mathrm {Ell}}$
.
$\operatorname {\mathrm {Spec}} A\to \mathcal {M}_{\mathrm {Ell}}$
.
Proof of Claim 5.3. As
![]() $\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p^\infty )\to \mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
is an ind-étale cover (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 5.1]), it is faithfully flat. By base-change, we see that
$\mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}(p^\infty )\to \mathcal {M}^{\mathrm {ord}}_{\mathrm {Ell}}$
is an ind-étale cover (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Lemma 5.1]), it is faithfully flat. By base-change, we see that
![]() $A^{\mathrm {ord}}\to W$
and
$A^{\mathrm {ord}}\to W$
and
![]() $(A^{\mathrm {ord}})^{\mathrm {ss}}\to W^{\mathrm {ss}}$
are also faithfully flat, and hence
$(A^{\mathrm {ord}})^{\mathrm {ss}}\to W^{\mathrm {ss}}$
are also faithfully flat, and hence
![]() $\widetilde {\alpha }$
is injective if we can show
$\widetilde {\alpha }$
is injective if we can show
![]() $\alpha $
is injective. To do this, we show
$\alpha $
is injective. To do this, we show
![]() $\alpha _\ast \colon A_\ast ^{\mathrm {ord}}\to (A_\ast ^{\mathrm {ss}})^{\mathrm {ord}}$
is injective. Using the notation above, we find ourselves with the following commutative diagram of graded rings, where all maps are the indicated localisations or completions:
$\alpha _\ast \colon A_\ast ^{\mathrm {ord}}\to (A_\ast ^{\mathrm {ss}})^{\mathrm {ord}}$
is injective. Using the notation above, we find ourselves with the following commutative diagram of graded rings, where all maps are the indicated localisations or completions:

Let us now make the following remarks from this diagram.
(1) From our choice of A, we have
![]() $A=A_1\times A_2$
, where
$A=A_1\times A_2$
, where
![]() $A_1$
represents
$A_1$
represents
![]() $\mathcal {M}_1(4)^{\mathrm {sm}}$
and
$\mathcal {M}_1(4)^{\mathrm {sm}}$
and
![]() $A_2$
represents
$A_2$
represents
![]() $\mathcal {M}_1(5)$
. Moreover, both
$\mathcal {M}_1(5)$
. Moreover, both
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are integral domains; see [Reference ZhuZhu14, Proposition 2.1] and [Reference Behrens and OrmsbyBO16, Theorem 1.1.1], respectively, where the following isomorphisms are constructed:
$A_2$
are integral domains; see [Reference ZhuZhu14, Proposition 2.1] and [Reference Behrens and OrmsbyBO16, Theorem 1.1.1], respectively, where the following isomorphisms are constructed:
It then follows that
![]() $\gamma $
can be written in the following commutative diagram of graded rings:
$\gamma $
can be written in the following commutative diagram of graded rings:

The ring A is Noetherian as it is finitely presented over
![]() $\operatorname {\mathrm {Spec}} \mathbf {Z}$
, so both
$\operatorname {\mathrm {Spec}} \mathbf {Z}$
, so both
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are Noetherian integral domains. In particular, the completion maps
$A_2$
are Noetherian integral domains. In particular, the completion maps
![]() $\gamma _i$
are flat for
$\gamma _i$
are flat for
![]() $i=1,2$
. If we know these maps
$i=1,2$
. If we know these maps
![]() $\gamma _i$
are nonzero, then it immediately follows that they are injective. To see that they are nonzero, it suffices to show that
$\gamma _i$
are nonzero, then it immediately follows that they are injective. To see that they are nonzero, it suffices to show that
![]() $v_1$
is not a unit inside both
$v_1$
is not a unit inside both
![]() $A_{\ast ,1}$
and
$A_{\ast ,1}$
and
![]() $A_{\ast ,2}$
. This is where our choice of A comes in. If our fixed prime
$A_{\ast ,2}$
. This is where our choice of A comes in. If our fixed prime
![]() $p\neq 2,5$
, then for both
$p\neq 2,5$
, then for both
![]() $i=1,2$
, the image of the map
$i=1,2$
, the image of the map
contains a supersingular elliptic curve, as all supersingular elliptic curves are contained in the smooth locus of
![]() $\widehat {\mathcal {M}}_{\mathrm {Ell}}$
. This implies that
$\widehat {\mathcal {M}}_{\mathrm {Ell}}$
. This implies that
![]() $v_1$
cannot be a unit, else
$v_1$
cannot be a unit, else
![]() $\operatorname {\mathrm {Spf}} \widehat {A}_i\to \widehat {\mathcal {M}}_{\mathrm {Ell}}$
would define only ordinary elliptic curves of height one. Similarly, if
$\operatorname {\mathrm {Spf}} \widehat {A}_i\to \widehat {\mathcal {M}}_{\mathrm {Ell}}$
would define only ordinary elliptic curves of height one. Similarly, if
![]() $p=2$
, then the p-completion of A is
$p=2$
, then the p-completion of A is
![]() $\widehat {A}_2$
, and we again see
$\widehat {A}_2$
, and we again see
![]() $v_1$
is not a unit so
$v_1$
is not a unit so
![]() $\gamma _2=\gamma $
is injective. The same holds for
$\gamma _2=\gamma $
is injective. The same holds for
![]() $\widehat {A}_1$
when
$\widehat {A}_1$
when
![]() $p=5$
. This implies that
$p=5$
. This implies that
![]() $\gamma _1\times \gamma _2$
is always injective, and hence
$\gamma _1\times \gamma _2$
is always injective, and hence
![]() $\gamma $
is injective.
$\gamma $
is injective.
(2) As
![]() $\beta $
is the
$\beta $
is the
![]() $v_1$
-localisation of
$v_1$
-localisation of
![]() $\gamma $
, and localisation is exact, we see that
$\gamma $
, and localisation is exact, we see that
![]() $\beta $
is also injective.
$\beta $
is also injective.
(3) Standard arguments show that the p-completion of
![]() $\beta $
, also known as
$\beta $
, also known as
![]() $\alpha _\ast $
, is also injective. Indeed, limits are left exact, so it suffices to show each
$\alpha _\ast $
, is also injective. Indeed, limits are left exact, so it suffices to show each
![]() $\alpha _\ast ^k$
in the following commutative diagram of rings is injective, for every
$\alpha _\ast ^k$
in the following commutative diagram of rings is injective, for every
![]() $k\geq 1$
:
$k\geq 1$
:

Given an element
![]() $\overline {x}$
such that
$\overline {x}$
such that
![]() $\alpha _\ast ^k(\overline {x})=0$
, then we first note that any lift x over
$\alpha _\ast ^k(\overline {x})=0$
, then we first note that any lift x over
![]() $\overline {x}$
is sent to a
$\overline {x}$
is sent to a
![]() $\beta (x)$
such that
$\beta (x)$
such that
![]() $p^k\beta (x)=0$
. However,
$p^k\beta (x)=0$
. However,
![]() $A^{\mathrm {ss}}_\ast [v_1^{-1}]$
is flat over
$A^{\mathrm {ss}}_\ast [v_1^{-1}]$
is flat over
![]() $\mathbf {Z}$
, as we have the following composite of flat maps:
$\mathbf {Z}$
, as we have the following composite of flat maps:
the second map is flat as
![]() $\operatorname {\mathrm {Spec}} A\to \mathcal {M}_{\mathrm {Ell}}$
is étale and
$\operatorname {\mathrm {Spec}} A\to \mathcal {M}_{\mathrm {Ell}}$
is étale and
![]() $\mathcal {M}_{\mathrm {Ell}}$
is smooth over
$\mathcal {M}_{\mathrm {Ell}}$
is smooth over
![]() $\mathbf {Z}$
, and the third map is flat as each
$\mathbf {Z}$
, and the third map is flat as each
![]() $\omega ^{\otimes k}_E(\operatorname {\mathrm {Spf}} A)$
is a line bundle and hence projective of rank 1. This implies that
$\omega ^{\otimes k}_E(\operatorname {\mathrm {Spf}} A)$
is a line bundle and hence projective of rank 1. This implies that
![]() $A^{\mathrm {ss}}_\ast [v_1^{-1}]$
is torsion-free, and hence
$A^{\mathrm {ss}}_\ast [v_1^{-1}]$
is torsion-free, and hence
![]() $\beta (x)=0$
. As
$\beta (x)=0$
. As
![]() $\beta $
is injective, this implies
$\beta $
is injective, this implies
![]() $x=0$
and
$x=0$
and
![]() $\overline {x}=0$
, and hence
$\overline {x}=0$
, and hence
![]() $\alpha _\ast ^k$
is injective.
$\alpha _\ast ^k$
is injective.
It follows that
![]() $\widetilde {\alpha }$
is injective.
$\widetilde {\alpha }$
is injective.
Proof for a general étale morphism. Let
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
be an arbitrary étale morphism and consider the Cartesian diagram of stacks
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
be an arbitrary étale morphism and consider the Cartesian diagram of stacks

where
![]() $\operatorname {\mathrm {Spec}} A=\mathcal {M}_1^{\mathrm {sm}}(4)\sqcup \mathcal {M}_1^{\mathrm {sm}}(5)$
is the stack of the previous paragraph and note that
$\operatorname {\mathrm {Spec}} A=\mathcal {M}_1^{\mathrm {sm}}(4)\sqcup \mathcal {M}_1^{\mathrm {sm}}(5)$
is the stack of the previous paragraph and note that
![]() $\operatorname {\mathrm {Spec}} B$
is affine as
$\operatorname {\mathrm {Spec}} B$
is affine as
![]() $\mathcal {M}_{\mathrm {Ell}}$
is separated; see part (2) of [Sta, Tag 01SG]. All of the morphisms above are étale by base-change, so we can consider the morphism of
$\mathcal {M}_{\mathrm {Ell}}$
is separated; see part (2) of [Sta, Tag 01SG]. All of the morphisms above are étale by base-change, so we can consider the morphism of
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\mathscr {O}(A)\to \mathscr {O}(B)$
.
$\mathscr {O}(A)\to \mathscr {O}(B)$
.
Claim 5.4. The morphism of
![]() $\mathbf {E}_\infty $
-rings
$\mathbf {E}_\infty $
-rings
![]() $\mathscr {O}(A)\to \mathscr {O}(B)$
is étale.
$\mathscr {O}(A)\to \mathscr {O}(B)$
is étale.
Proof. Recall from [Reference LurieLur17, Section 7.5] that a morphism
![]() $\mathcal {A}\to \mathcal {B}$
of
$\mathcal {A}\to \mathcal {B}$
of
![]() $\mathbf {E}_\infty $
-rings is étale if the morphism
$\mathbf {E}_\infty $
-rings is étale if the morphism
![]() $\pi _0 \mathcal {A}\to \pi _0 \mathcal {B}$
of discrete commutative rings is étale and the natural map of
$\pi _0 \mathcal {A}\to \pi _0 \mathcal {B}$
of discrete commutative rings is étale and the natural map of
![]() $\pi _0 \mathcal {B}$
-modules
$\pi _0 \mathcal {B}$
-modules
is an isomorphism. The fact that
![]() $\pi _0 \mathscr {O}(A)\to \pi _0 \mathscr {O}(B)$
is étale follows from the facts that
$\pi _0 \mathscr {O}(A)\to \pi _0 \mathscr {O}(B)$
is étale follows from the facts that
![]() $A\to B$
is étale and
$A\to B$
is étale and
![]() $\mathscr {O}$
defines natural elliptic cohomology theories. The condition on the higher homotopy groups also follows as
$\mathscr {O}$
defines natural elliptic cohomology theories. The condition on the higher homotopy groups also follows as
![]() $\mathscr {O}$
defines natural elliptic cohomology theories; see Remark 2.4.
$\mathscr {O}$
defines natural elliptic cohomology theories; see Remark 2.4.
By [Reference LurieLur17, Theorem 7.5.0.6], the
![]() $\pi _0$
-functor induces an equivalence of
$\pi _0$
-functor induces an equivalence of
![]() $\infty $
-categories
$\infty $
-categories
where the superscript indicates subcategories of étale algebras. By Claim 5.4, for any étale
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\mathscr {O}(A)$
-algebra
$\mathscr {O}(A)$
-algebra
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
![]() $\pi _0 \mathcal {B}$
is isomorphic to B as an A-algebra, there is an equivalence of
$\pi _0 \mathcal {B}$
is isomorphic to B as an A-algebra, there is an equivalence of
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\mathscr {O}(A)$
-algebras
$\mathscr {O}(A)$
-algebras
![]() $\mathscr {O}(B)\simeq \mathcal {B}$
, which is unique up to contractible choice. As we have proven Lemma 5.1 for
$\mathscr {O}(B)\simeq \mathcal {B}$
, which is unique up to contractible choice. As we have proven Lemma 5.1 for
![]() $\operatorname {\mathrm {Spec}} A$
, it follows from the proof of Theorem 2.1 above that the equivalence of homotopy commutative ring spectra
$\operatorname {\mathrm {Spec}} A$
, it follows from the proof of Theorem 2.1 above that the equivalence of homotopy commutative ring spectra
![]() $\mathrm {h}\phi (A)\colon \mathscr {O}^{\mathrm {top}}(A)\simeq \mathscr {O}(A)$
can be lifted to a morphism of
$\mathrm {h}\phi (A)\colon \mathscr {O}^{\mathrm {top}}(A)\simeq \mathscr {O}(A)$
can be lifted to a morphism of
![]() $\mathbf {E}_\infty $
-rings. The composite
$\mathbf {E}_\infty $
-rings. The composite
![]() $\mathscr {O}(A)\simeq \mathscr {O}^{\mathrm {top}}(A)\to \mathscr {O}^{\mathrm {top}}(B)$
is also an étale
$\mathscr {O}(A)\simeq \mathscr {O}^{\mathrm {top}}(A)\to \mathscr {O}^{\mathrm {top}}(B)$
is also an étale
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\mathscr {O}(A)$
-algebra recognising B, and hence we obtain a natural equivalence of
$\mathscr {O}(A)$
-algebra recognising B, and hence we obtain a natural equivalence of
![]() $\mathbf {E}_\infty $
-
$\mathbf {E}_\infty $
-
![]() $\mathscr {O}(A)$
-algebras
$\mathscr {O}(A)$
-algebras
![]() $\mathscr {O}^{\mathrm {top}}(B)\simeq \mathscr {O}(B)$
. As
$\mathscr {O}^{\mathrm {top}}(B)\simeq \mathscr {O}(B)$
. As
![]() $\mathscr {O}^{\mathrm {top}}(B)$
is
$\mathscr {O}^{\mathrm {top}}(B)$
is
![]() $\theta $
-compatible (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 6.3]), we see
$\theta $
-compatible (see [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Remark 6.3]), we see
![]() $\mathscr {O}(B)$
is also
$\mathscr {O}(B)$
is also
![]() $\theta $
-compatible, meaning that Equation (5-2) commutes for
$\theta $
-compatible, meaning that Equation (5-2) commutes for
![]() $R=B$
. Finally, let us turn our attention to
$R=B$
. Finally, let us turn our attention to
![]() $\mathscr {O}(R)\to \mathscr {O}(B)$
.
$\mathscr {O}(R)\to \mathscr {O}(B)$
.
Claim 5.5. The morphism induced by
![]() $\mathscr {O}(R)\to \mathscr {O}(B)$
on zeroth p-adic K-theory is injective.
$\mathscr {O}(R)\to \mathscr {O}(B)$
on zeroth p-adic K-theory is injective.
Assuming the above claim, it immediately follows that Equation (5-2) commutes for our arbitrary R. Indeed, Claim 5.5 provides us with an injection of
![]() $\theta $
-algebras induced by
$\theta $
-algebras induced by
![]() $\mathscr {O}(R)\to \mathscr {O}(B)$
, which allows us to check the commutativity of Equation (5-2) in the same diagram for
$\mathscr {O}(R)\to \mathscr {O}(B)$
, which allows us to check the commutativity of Equation (5-2) in the same diagram for
![]() $R=B$
, which we know commutes by the above paragraph.
$R=B$
, which we know commutes by the above paragraph.
Proof of Claim 5.5. The morphism
![]() $\operatorname {\mathrm {Spec}} B\to \operatorname {\mathrm {Spec}} R$
can be factored into the following diagram of formal stacks:
$\operatorname {\mathrm {Spec}} B\to \operatorname {\mathrm {Spec}} R$
can be factored into the following diagram of formal stacks:

Every square above is Cartesian, and the
![]() $\widehat {(-)}$
indicates base-change over
$\widehat {(-)}$
indicates base-change over
![]() $\operatorname {\mathrm {Spf}}\mathbf {Z}_p$
. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 6.1], the morphism
$\operatorname {\mathrm {Spf}}\mathbf {Z}_p$
. By [Reference Douglas, Francis, Henriques and HillDFHH14, Section 12 and Proposition 6.1], the morphism
![]() $W_R\to W_B$
above is isomorphic to the morphism induced by
$W_R\to W_B$
above is isomorphic to the morphism induced by
![]() $\mathscr {O}(R)\to \mathscr {O}(B)$
on p-adic K-theory, and hence it suffices to see the composite map
$\mathscr {O}(R)\to \mathscr {O}(B)$
on p-adic K-theory, and hence it suffices to see the composite map
featured in the upper-left corner of Equation (5-4), is injective. As
![]() $\operatorname {\mathrm {Spec}} A\to \mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
is an étale cover, then by base-change, we see
$\operatorname {\mathrm {Spec}} A\to \mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
is an étale cover, then by base-change, we see
![]() $W^{\mathrm {sm}}_R\to W_B$
is also faithfully flat and hence injective. Observe that
$W^{\mathrm {sm}}_R\to W_B$
is also faithfully flat and hence injective. Observe that
![]() $W_R\to W_R^{\mathrm {sm}}$
is an open immersion of formal affine schemes by base-change as
$W_R\to W_R^{\mathrm {sm}}$
is an open immersion of formal affine schemes by base-change as
![]() $\mathcal {M}^{\mathrm {sm}}_{\mathrm {Ell}}\to \mathcal {M}_{\mathrm {Ell}}$
is an open immersion of stacks. Moreover, we claim the open immersion
$\mathcal {M}^{\mathrm {sm}}_{\mathrm {Ell}}\to \mathcal {M}_{\mathrm {Ell}}$
is an open immersion of stacks. Moreover, we claim the open immersion
![]() $R\to R^{\mathrm {sm}}$
has scheme theoretically dense image as
$R\to R^{\mathrm {sm}}$
has scheme theoretically dense image as
![]() $\Delta $
is a nonzero divisor in R; see [Sta, Tag 01RE]. Indeed, to see
$\Delta $
is a nonzero divisor in R; see [Sta, Tag 01RE]. Indeed, to see
![]() $\Delta $
is not a zero divisor, it suffices to show that the image of
$\Delta $
is not a zero divisor, it suffices to show that the image of
![]() $\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
has nontrivial intersection with the image of
$\operatorname {\mathrm {Spec}} R\to \mathcal {M}_{\mathrm {Ell}}$
has nontrivial intersection with the image of
![]() $\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
. This is clear on the level of underlying topological spaces, as the inclusion
$\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}$
. This is clear on the level of underlying topological spaces, as the inclusion
![]() $|\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}|\to |\mathcal {M}_{\mathrm {Ell}}|$
is equivalent to open immersion of coarse moduli spaces
$|\mathcal {M}_{\mathrm {Ell}}^{\mathrm {sm}}|\to |\mathcal {M}_{\mathrm {Ell}}|$
is equivalent to open immersion of coarse moduli spaces
![]() $|\mathbf {A}^1_{\mathbf {Z}}|\to |\mathbf {P}^1_{\mathbf {Z}}|$
which adds the point at
$|\mathbf {A}^1_{\mathbf {Z}}|\to |\mathbf {P}^1_{\mathbf {Z}}|$
which adds the point at
![]() $\infty $
, and the map
$\infty $
, and the map
![]() $|\operatorname {\mathrm {Spec}} R|\to |\mathcal {M}_{\mathrm {Ell}}|$
is open as étale morphisms are in particular flat and locally of finite presentation; see [Sta, Tag 06R7]. As all the right vertical maps in Equation (5-4) are flat, and
$|\operatorname {\mathrm {Spec}} R|\to |\mathcal {M}_{\mathrm {Ell}}|$
is open as étale morphisms are in particular flat and locally of finite presentation; see [Sta, Tag 06R7]. As all the right vertical maps in Equation (5-4) are flat, and
![]() $R\to R^{\mathrm {sm}}$
is quasi-compact (as a map of affine schemes), then [Sta, Tag 0CMK] tells us that
$R\to R^{\mathrm {sm}}$
is quasi-compact (as a map of affine schemes), then [Sta, Tag 0CMK] tells us that
![]() $W_R\to W_R^{\mathrm {sm}}$
also has scheme theoretically dense image. Another application of [Sta, Tag 01RE] shows this open immersion
$W_R\to W_R^{\mathrm {sm}}$
also has scheme theoretically dense image. Another application of [Sta, Tag 01RE] shows this open immersion
![]() $W_R\to W_R^{\mathrm {sm}}$
must be injective. Therefore, the composite in Equation (5-5) is injective.
$W_R\to W_R^{\mathrm {sm}}$
must be injective. Therefore, the composite in Equation (5-5) is injective.
This finishes our proof of Lemma 5.1.
Remark 5.6. There is a potential improvement that could be made to this article. If the reader can find an affine étale cover
![]() $\operatorname {\mathrm {Spec}} A\to \mathcal {M}_{\mathrm {Ell}}$
such that the analogous Claim 5.3 holds, which is a purely algebro-geometric pursuit, then the rest of Theorem 2.1 follows formally. Indeed, in this case, one can prove that
$\operatorname {\mathrm {Spec}} A\to \mathcal {M}_{\mathrm {Ell}}$
such that the analogous Claim 5.3 holds, which is a purely algebro-geometric pursuit, then the rest of Theorem 2.1 follows formally. Indeed, in this case, one can prove that
![]() $\mathscr {O}^{\mathrm {top}}$
is uniquely defined on the Čech nerve of such a cover by copying the proofs of Theorem 2.1 and Lemma 5.1 seen above. One can then use spectral deformation theory and descent to show that Theorem 2.1 follows from this particular case. With this in mind, the reader might also notice that restricting Theorem 1.3 to the moduli stack of smooth elliptic curves vastly simplifies the above proof.
$\mathscr {O}^{\mathrm {top}}$
is uniquely defined on the Čech nerve of such a cover by copying the proofs of Theorem 2.1 and Lemma 5.1 seen above. One can then use spectral deformation theory and descent to show that Theorem 2.1 follows from this particular case. With this in mind, the reader might also notice that restricting Theorem 1.3 to the moduli stack of smooth elliptic curves vastly simplifies the above proof.
Acknowledgements
I owe a huge thank you to Lennart Meier for teaching me everything I know about
![]() $\mathscr {O}^{\mathrm {top}}$
. Also thank you to the anonymous referee for their attention to detail and suggestions to improve this article.
$\mathscr {O}^{\mathrm {top}}$
. Also thank you to the anonymous referee for their attention to detail and suggestions to improve this article.