Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T15:30:18.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Elements of rings and Banach algebras with related spectral idempotents

Part of: Basic linear algebra

Published online by Cambridge University Press:  09 April 2009

N. Castro-González  and
J. Y. Vélez-Cerrada
N. Castro-González
Affiliation:
Facultad de Informática, Universidad Politécnica de Madrid, 28660 Boadilla del Monte, Madrid, Spain, e-mail: [email protected], [email protected]
J. Y. Vélez-Cerrada
Affiliation:
Facultad de Informática, Universidad Politécnica de Madrid, 28660 Boadilla del Monte, Madrid, Spain, e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let aπ denote the spectral idempotent of a generalized Drazin invertible element a of a ring. We characterize elements b such that 1 − (bπ − aπ)2 is invertible. We also apply this result in rings with involution to obtain a characterization of the perturbation of EP elements. In Banach algebras we obtain a characterization in terms of matrix representations and derive error bounds for the perturbation of the Drazin Inverse. This work extends recent results for matrices given by the same authors to the setting of rings and Banach algebras. Finally, we characterize generalized Drazin invertible operators A, B ∈ 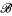(X) such that pr(Bπ) = pr(Aπ + S), where pr is the natural homomorphism of 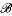(X) onto the Calkin algebra and S ∈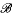(X) is given.

2000 Mathematics subject classification: primary 16A32, 16A28, 15A09.

Keywords

Generalized Drazin inversespectral idempotentEP elementsperturbationFredholm operators.

MSC classification

Secondary: 15A09: Matrix inversion, generalized inverses
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 80 , Issue 3 , June 2006 , pp. 383 - 396
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Caradus, S. R., Pfaffenberger, W. E. and Yood, B., Calkin algebras and algebras of operators on Banach spaces, Lecture Notes in Pure and Applied Mathematics 9 (Marcel Dekker, New York, 1974).Google Scholar
[2]Castro-González, N. and Koliha, J. J., ‘New additive results for the g-Drazin Inverse’, Proc. Roy. Soc. Edinburgh Sect. A 134 (2004), 1085–1097.Google Scholar
[3]Castro-González, N., Koliha, J. J. and Rakočević, V., ‘Continuity and general perturbation of the Drazin inverse for closed operators’, Abstr. Appl. Anal. 6 (2002), 335–347.CrossRefGoogle Scholar
[4]Castro-González, N., Koliha, J. J. and Wei, Y., ‘Perturbation of the Drazin inverse for matrices with equal eigenprojection at zero’, Linear Algebra Appl. 312 (2000), 181–189.Google Scholar
[5]Castro-González, N., Koliha, J. J. and Wei, Y., ‘Error bounds for perturbation of the Drazin inverse of closed operators with equal spectral projections’, Appl. Anal. 81 (2002), 915–928.Google Scholar
[6]Castro-González, N. and Vélez-Cerrada, J. Y., ‘Characterizations of matrices which eigenprojections at zero are equal to a fixed perturbation’, Appl. Math. Comput. 159 (2004), 613–623.Google Scholar
[7]Rakočević, V., ‘Koliha-Drazin invertible operators and commuting Riesz perturbations’, Acta Sci. Math. (Szeged) 68 (2002), 291–301.Google Scholar
[8]Rakočević, V. and Wei, Y., ‘The perturbation theory for the drazin inverse and its aplications II’, J. Aust. Math. Soc. 69 (2000), 1–9.Google Scholar
[9]Drazin, M. P., ‘Pseudo-inverses in associate rings and semigroups’, Amer. Math. Monthly 65 (1958), 506–514.Google Scholar
[10]Harte, R. E., ‘On quasinilpotents in rings’, Panamer. Math. J. 1 (1991), 10–16.Google Scholar
[11]Hartwig, R. E., ‘Block generalized inverses’, Arch. Ration. Mech. Anal. 61 (1976), 197–251.Google Scholar
[12]Koliha, J. J., ‘A generalized Drazin inverse’, Glasgow Math. J. 38 (1996), 367–381.Google Scholar
[13]Koliha, J. J., ‘Elements of C*-algebras commuting with their Moore-Penrose inverse’, Studia Math. 139 (2000), 81–90.Google Scholar
[14]Koliha, J. J., ‘Error bound for a general perturbation of the Drazin inverse’, Appl. Math. Comput. 126 (2002), 181–185.Google Scholar
[15]Koliha, J. J. and Patrício, P., ‘Elements of rings with equal spectral idempotents’, J. Aust. Math. Soc. 72 (2002), 137–152.Google Scholar
[16]Li, X. and Wei, Y., ‘An improvement on the perturbation of the group inverse and oblique projection’, LinearAlgebra Appl. 338 (2001), 53–66.Google Scholar
[17]Wei, Y. and Li, X., ‘An improvement on the perturbation bounds for the Drazin inverse’, Numer. Linear Algebra Appl. 10 (2003), 563–575.Google Scholar
[18]Wei, Y. and Wang, G., ‘The perturbation theory for the Drazin inverse and its aplications’, Linear Algebra Appl. 258 (1997), 179–186.Google Scholar