Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lettl, Günter
Pethő, Attila
and
Voutier, Paul
1999.
Simple families of Thue inequalities.
Transactions of the American Mathematical Society,
Vol. 351,
Issue. 5,
p.
1871.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
209.
Bennett, Michael A.
and
Reznick, Bruce
2004.
Positive Rational Solutions toxy=ymx: A Number-Theoretic Excursion.
The American Mathematical Monthly,
Vol. 111,
Issue. 1,
p.
13.
Everest, Graham
Mclaren, Gerard
and
Ward, Thomas
2006.
Primitive divisors of elliptic divisibility sequences.
Journal of Number Theory,
Vol. 118,
Issue. 1,
p.
71.
Ingram, Patrick
2007.
Diophantine analysis and torsion on elliptic curves.
Proceedings of the London Mathematical Society,
Vol. 94,
Issue. 1,
p.
137.
Bennett, Michael A.
2007.
The Diophantine equation (xk − 1)(yk − 1) = (zk − 1)t.
Indagationes Mathematicae,
Vol. 18,
Issue. 4,
p.
507.
BENNETT, MICHAEL A.
BUGEAUD, YANN
and
MIGNOTTE, MAURICE
2012.
Perfect powers with few binary digits and related Diophantine problems, II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 153,
Issue. 3,
p.
525.
Rábai, Zs.
Bennett, M.A.
and
Pink, I.
2013.
On the number of solutions of binomial Thue inequalities.
Electronic Notes in Discrete Mathematics,
Vol. 43,
Issue. ,
p.
299.
Rout, S. S.
2014.
On Second Order Gap Balancing Numbers.
Journal of Numbers,
Vol. 2014,
Issue. ,
p.
1.
Filaseta, M.
Graham, S.
and
Trifonov, O.
2015.
Starting with gaps between k-free numbers.
International Journal of Number Theory,
Vol. 11,
Issue. 05,
p.
1411.
Bennett, Michael A.
2017.
The polynomial–exponential equation $$1+2^a+6^b=y^q$$ 1 + 2 a + 6 b = y q.
Periodica Mathematica Hungarica,
Vol. 75,
Issue. 2,
p.
387.
Carević, Miroslava Mihajlov
Petrović, Milena
and
Denić, Nebojša
2019.
Figurative Numbers Contribution in Perceiving the Legality in Numerous Strings Tasks and Long-term Memory of Numerous Data.
EURASIA Journal of Mathematics, Science and Technology Education,
Vol. 15,
Issue. 4,
Nguyen, Khoa Dang
2019.
The Hermite–Joubert Problem and a Conjecture of Brassil and Reichstein.
Canadian Mathematical Bulletin,
Vol. 62,
Issue. 1,
p.
169.
Waldschmidt, Michel
2020.
Class Groups of Number Fields and Related Topics.
p.
25.
Mihajlov-Carević, Miroslava
Milojević, Nataša
and
Rešić, Sead
2021.
Visualization of solving problems with sequences of numbers: Statistical comparison of the two methods.
Trendovi u poslovanju,
Vol. 9,
Issue. 2,
p.
75.
Kawashima, Makoto
and
Poëls, Anthony
2023.
Padé approximation for a class of hypergeometric functions and parametric geometry of numbers.
Journal of Number Theory,
Vol. 243,
Issue. ,
p.
646.
Hirata-Kohno, Noriko
Kawashima, Makoto
Poëls, Anthony
and
Washio, Yukiko
2023.
S-unit equation in two variables and Padé approximations.
International Journal of Number Theory,
Vol. 19,
Issue. 10,
p.
2427.
Badziahin, Dzmitry
2024.
On effective irrationality exponents of cubic irrationals.
The Ramanujan Journal,
Vol. 64,
Issue. 4,
p.
1457.


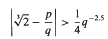 for any non-zero integers
for any non-zero integers 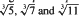 . Some Diophantine consequences are briefly discussed.
. Some Diophantine consequences are briefly discussed.