Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T01:07:40.117Z Has data issue: false hasContentIssue false
  • English
  • Français

A DUALIZING OBJECT APPROACH TO NONCOMMUTATIVE STONE DUALITY

Part of: Basic constructions Special categories

Published online by Cambridge University Press:  19 August 2013

GANNA KUDRYAVTSEVA
GANNA KUDRYAVTSEVA*
Affiliation:
Faculty of Computer and Information Science, University of Ljubljana, Tržaška cesta, 25, SI-1001, Ljubljana, Slovenia
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of the present paper is to extend the dualizing object approach to Stone duality to the noncommutative setting of skew Boolean algebras. This continues the study of noncommutative generalizations of different forms of Stone duality initiated in recent papers by Bauer and Cvetko-Vah, Lawson, Lawson and Lenz, Resende, and also the current author. In this paper we construct a series of dual adjunctions between the categories of left-handed skew Boolean algebras and Boolean spaces, the unital versions of which are induced by dualizing objects 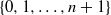$\{ 0, 1, \ldots , n+ 1\} $, 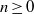$n\geq 0$. We describe the categories of Eilenberg-Moore algebras of the monads of the adjunctions and construct easily understood noncommutative reflections of left-handed skew Boolean algebras, where the latter can be faithfully embedded (if 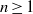$n\geq 1$) in a canonical way. As an application, we answer the question that arose in a recent paper by Leech and Spinks to describe the left adjoint to their ‘twisted product’ functor 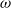$\omega $.

Keywords

Boolean spaceBoolean algebraStone dualityskew Boolean algebraétale spacedualizing objectschizophrenic objectadjunctionmonadEilenberg–Moore algebrareflective subcategory

MSC classification

Secondary: 06E15: Stone spaces (Boolean spaces) and related structures 06E75: Generalizations of Boolean algebras 18B30: Categories of topological spaces and continuous mappings 54B40: Presheaves and sheaves
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 3 , December 2013 , pp. 383 - 403
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Awodey, S., Category Theory (Oxford University Press, New York, 2006).CrossRefGoogle Scholar
Bauer, A. and Cvetko-Vah, K., ‘Stone duality for skew Boolean algebras with intersections’, Houston J. Math. 39 (1) (2013), 73–109.Google Scholar
Bauer, A., Cvetko-Vah, K., Gehrke, M., van Gool, S. and Kudryavtseva, G., ‘A noncommutative Priestley duality’. arXiv:1206.5848.Google Scholar
Bignall, R. J. and Leech, J. E., ‘Skew Boolean algebras and discriminator varieties’, Algebra Universalis 33 (1995), 387–398.CrossRefGoogle Scholar
Bredon, G. E., Sheaf Theory, Graduate Texts in Mathematics, 170 (Springer-Verlag, New York, 1997).CrossRefGoogle Scholar
Burris, S. and Sankappanavar, H. P., A Course in Universal Algebra, Graduate Texts in Mathematics, 78 (Springer-Verlag, New York–Berlin, 1981).CrossRefGoogle Scholar
Clark, D. M. and Davey, B. A., Natural Dualities for the Working Algebraist (Cambridge University Press, Cambridge, 1998).Google Scholar
Cornish, W. H., ‘Boolean skew algebras’, Acta Math. Acad. Sci. Hungar. 36 (1980), 281–291.CrossRefGoogle Scholar
Doctor, H. P., ‘The categories of Boolean lattices, Boolean rings and Boolean spaces’, Canad. Math. Bull. 7 (1964), 245–252.CrossRefGoogle Scholar
Funk, J., ‘Semigroups and toposes’, Semigroup Forum 75 (3) (2007), 481–520.CrossRefGoogle Scholar
Funk, J. and Hofstra, P., ‘Topos theoretic aspects of semigroup actions’, Theory Appl. Categ. 24 (6) (2010), 117–147.Google Scholar
Funk, J., Lawson, M. V. and Steinberg, B., ‘Characterizations of Morita equivalent inverse semigroups’, J. Pure Appl. Algebra 215 (9) (2011), 2262–2279.CrossRefGoogle Scholar
Funk, J. and Steinberg, B., ‘The universal covering of an inverse semigroup’, Appl. Categ. Structures 18 (2) (2010), 135–163.CrossRefGoogle Scholar
Givant, S. and Halmos, P., Introduction to Boolean Algebras, Undergraduate Texts in Mathematics (Springer, New York, 2009).Google Scholar
Johnstone, P. T., Stone Spaces (Cambridge University Press, Cambridge, 1986).Google Scholar
Kudryavtseva, G., ‘A refinement of Stone duality to skew Boolean algebras’, Algebra Universalis 67 (2012), 397–416.CrossRefGoogle Scholar
Kudryavtseva, G. and Lawson, M. V., ‘The structure of generalized inverse semigroups’, Semigroup Forum, to appear; arXiv:1207.4296.Google Scholar
Kudryavtseva, G. and Lawson, M. V., ‘The classifying space of an inverse semigroup’. arXiv:1210.4421.Google Scholar
Kudryavtseva, G. and Lawson, M. V., ‘Stone duality for generalized inverse semigroups’, in preparation.Google Scholar
Lawson, M. V., ‘A noncommutative generalization of Stone duality’, J. Aust. Math. Soc. 88 (2010), 385–404.CrossRefGoogle Scholar
Lawson, M. V., ‘Non-commutative Stone duality: inverse semigroups, topological groupoids and ${C}^{\star } $-algebras’, Internat. J. Algebra Comput. 22 (6) (2012).CrossRefGoogle Scholar
Lawson, M. V. and Lenz, D. H., ‘Pseudogroups and their étale groupoids’, Adv. Math. 244 (2013), 117–170.CrossRefGoogle Scholar
Leech, J., ‘Skew lattices in rings’, Algebra Universalis 26 (1989), 48–72.CrossRefGoogle Scholar
Leech, J., ‘Skew Boolean Algebras’, Algebra Universalis 27 (1990), 497–506.CrossRefGoogle Scholar
Leech, J., ‘Normal Skew lattices’, Semigroup Forum 44 (1992), 1–8.CrossRefGoogle Scholar
Leech, J., ‘Recent developments in the theory of skew lattices’, Semigroup Forum 52 (1996), 7–24.CrossRefGoogle Scholar
Leech, J. and Spinks, M., ‘Skew Boolean algebras derived from Boolean algebras’, Algebra Universalis 58 (3) (2008), 287–302.CrossRefGoogle Scholar
Mac Lane, S., Categories for the Working Mathematician, Graduate Texts in Mathematics, 5 (Springer-Verlag, New York, 1998).Google Scholar
Mac Lane, S. and Moerdijk, I., ‘Sheaves in geometry and logic’, in: A First Introduction to Topos Theory (Springer, New York, 1994).Google Scholar
Porst, H.-E. and Tholen, W., ‘Concrete dualities’, in: Category Theory at Work (Heldermann Verlag, Berlin, 1991), 111–136.Google Scholar
Resende, P., ‘Étale groupoids and their quantales’, Adv. Math. 208 (2007), 147–209.CrossRefGoogle Scholar
Resende, P., ‘Lectures on étale groupoids, inverse semigroups and quantales’, Preprint available at www.math.ist.utl.pt.Google Scholar
Steinberg, B., ‘Strong Morita equivalence of inverse semigroups’, Houston J. Math. 37 (2011), 895–927.Google Scholar
Stone, M. H., ‘Applications of the theory of Boolean rings to general topology’, Trans. Amer. Math. Soc. 41 (1937), 375–481.CrossRefGoogle Scholar