Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T09:04:44.777Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DISTRIBUTIVITY SPECTRUM OF BAKER’S VARIETY

Part of: Lattices Varieties

Published online by Cambridge University Press:  26 October 2020

PAOLO LIPPARINI Open the ORCID record for PAOLO LIPPARINI [Opens in a new window]
PAOLO LIPPARINI*
Affiliation:
Dipartimento Fornace di Matematica, Viale della Ricerca Scientifica, Università di Roma ‘Tor Vergata’, I-00133RomeItaly
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For every n, we evaluate the smallest k such that the congruence inclusion 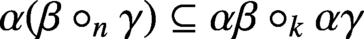$\alpha (\beta \circ _n \gamma ) \subseteq \alpha \beta \circ _{k} \alpha \gamma $ holds in a variety of reducts of lattices introduced by K. Baker. We also study varieties with a near-unanimity term and discuss identities dealing with reflexive and admissible relations.

Keywords

Baker’s varietyJónsson distributivity spectrumcongruence identityrelation identitycongruence distributive varietynear-unanimity termedge term

MSC classification

Primary: 08B10: Congruence modularity, congruence distributivity
Secondary: 06B75: Generalizations of lattices
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 1 , February 2021 , pp. 119 - 144
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by James East

Work performed under the auspices of G.N.S.A.G.A. Work supported by PRIN 2012 ‘Logica, Modelli e Insiemi’. The author acknowledges the MIUR Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006.

References

Baker, K. A., ‘Congruence-distributive polynomial reducts of lattices’, Algebra Universalis 9 (1979), 142–145.CrossRefGoogle Scholar
Barto, L. and Kozik, M., ‘Absorption in universal algebra and CSP ’, in: The Constraint Satisfaction Problem: Complexity and Approximability, Dagstuhl Follow-Ups, 7 (Schloss Dagstuhl–Leibniz Zentrum für Informatik, Wadern, 2017), 45–77.Google Scholar
Bergman, C., Universal Algebra: Fundamentals and Selected Topics (CRC Press, Boca Raton, FL, 2012).Google Scholar
Berman, J., Idziak, P., Marković, P., McKenzie, R., Valeriote, M. and Willard, R., ‘Varieties with few subalgebras of powers ’, Trans. Amer. Math. Soc. 362 (2010), 1445–1473.CrossRefGoogle Scholar
Burris, B. and Sankappanavar, H. P., A Course in Universal Algebra (Springer, New York, 1981).CrossRefGoogle Scholar
Czédli, G. and Horváth, E. K., ‘Congruence distributivity and modularity permit tolerances, Acta Univ. Palack. Olomuc. Fac. Rerum Natur. Math. 41 (2002), 39–42.Google Scholar
Czédli, G., Horváth, E. K. and Lipparini, P., ‘Optimal Mal’tsev conditions for congruence modular varieties ’, Algebra Universalis 53 (2005), 267–279.Google Scholar
Day, A., ‘A characterization of modularity for congruence lattices of algebras’, Canad. Math. Bull. 12 (1969), 167–173.Google Scholar
Freese, R., ‘Alan Day’s early work: congruence identities’, Algebra Universalis 34 (1995), 4–23.CrossRefGoogle Scholar
Freese, R. and Valeriote, M. A., ‘On the complexity of some Maltsev conditions ’, Int. J. Algebra Comput. 19 (2009), 41–77.CrossRefGoogle Scholar
Grätzer, G., Universal Algebra , 2nd expanded edn (Springer, New York, 1979).Google Scholar
Gumm, H. P., ‘Geometrical methods in congruence modular algebras ’, Mem. Amer. Math. Soc. 45(286) (1983) viii+79. Google Scholar
Hutchinson, G., ‘Relation categories and coproduct congruence categories in universal algebra ’, Algebra Universalis, 32 (1994), 609–647.CrossRefGoogle Scholar
Ježek, J., Universal Algebra (2008), available at http://ka.karlin.mff.cuni.cz/jezek/ua.pdf.Google Scholar
Jónsson, B., ‘Algebras whose congruence lattices are distributive’, Math. Scand. 21 (1967), 110–121.CrossRefGoogle Scholar
Jónsson, B., ‘Congruence varieties ’, Algebra Universalis 10 (1980), 355–394.CrossRefGoogle Scholar
Kaarli, K. and Pixley, A. F., Polynomial Completeness in Algebraic Systems (Chapman & Hall/CRC, Boca Raton, FL, 2001).Google Scholar
Kazda, A., Kozik, M., McKenzie, R. and Moore, M., ‘Absorption and directed Jónsson terms ’, in: Don Pigozzi on Abstract Algebraic Logic, Universal Algebra, and Computer Science, Outstanding Contributions to Logic, 16 (ed. Czelakowski, J.) (Springer, Cham, 2018), 203–220.CrossRefGoogle Scholar
Kearnes, K. A. and Szendrei, Á., ‘Clones of algebras with parallelogram terms ’, Internat. J. Algebra Comput. 22(1250005) (2012), 30.CrossRefGoogle Scholar
Lipparini, P., ‘From congruence identities to tolerance identities ’, Acta Sci. Math. (Szeged) 73 (2007), 31–51.Google Scholar
Lipparini, P. Relation identities equivalent to congruence modularity, Preprint, 2017, arXiv:1704.05274.Google Scholar
Lipparini, P. The distributivity spectrum of Baker’s variety, Preprint, 2017, arXiv:1709.05721v2.Google Scholar
Lipparini, P. On the number of terms witnessing congruence modularity, Preprint, 2017, arXiv:1709.06023.Google Scholar
Lipparini, P., ‘The Jónsson distributivity spectrum ’, Algebra Universalis 79(23) (2018), 1–16.CrossRefGoogle Scholar
Lipparini, P., ‘Unions of admissible relations and congruence distributivity’, Acta Math. Univ. Comenian. (N.S.) 87(2) (2018), 251–266.Google Scholar
Lipparini, P., ‘A variety $\mathbf{\mathcal{V}}$ is congruence modular if and only if $\mathbf{\mathcal{V}}$ satisfies $\varTheta \left(R\circ R\right)\subseteq {\left(\varTheta R\right)}^h$ , for some $h$ ’, in: Algebras and Lattice in Hawai’i A Conference in Honor of Ralph Freese, William Lampe, and J.B. Nation (eds. Adaricheva, K., DeMeo, W. and Hyndman, J.) (Lulu.com, Morrisville, NC, 2018), 61–65, available at https://universalalgebra.github.io/ALH-2018/assets/ALH-2018-proceedings-6x9.pdf.Google Scholar
Lipparini, P., ‘Relation identities in 3-distributive varieties ’, Algebra Universalis 80(55) (2019), 1–20.CrossRefGoogle Scholar
McKenzie, R. N., McNulty, G. F. and Taylor, W. F., Algebras, Lattices, Varieties, Vol. 1 (Wadsworth & Brooks/Cole Advanced Books & Software, Monterey, CA, 1987).Google Scholar
Mitschke, A., ‘Near unanimity identities and congruence distributivity in equational classes ’, Algebra Universalis 8 (1978), 29–32.CrossRefGoogle Scholar
Tschantz, S. T., ‘More conditions equivalent to congruence modularity ’, in: Universal Algebra and Lattice Theory, Lecture Notes in Mathematics, 1149 (Springer, Berlin, 1985), 270–282.CrossRefGoogle Scholar
Werner, H., ‘A Mal’cev condition for admissible relations ’, Algebra Universalis 3 (1973), 263.Google Scholar