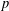Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T10:00:12.207Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTALITY OF CERTAIN ACTIONS ON $p$-ADIC SPHERES

Part of: Semigroups Lie groups Topological dynamics Linear algebraic groups and related topics

Published online by Cambridge University Press:  29 July 2019

RIDDHI SHAH Open the ORCID record for RIDDHI SHAH [Opens in a new window]  and
ALOK KUMAR YADAV Open the ORCID record for ALOK KUMAR YADAV [Opens in a new window]
RIDDHI SHAH
Affiliation:
School of Physical Sciences,Jawaharlal Nehru University, New Delhi 110067, India email [email protected], [email protected]
ALOK KUMAR YADAV*
Affiliation:
School of Physical Sciences,Jawaharlal Nehru University, New Delhi 110067, India email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the action of 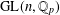$\operatorname{GL}(n,\mathbb{Q}_{p})$ on the 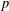$p$-adic unit sphere 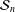${\mathcal{S}}_{n}$ arising from the linear action on 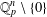$\mathbb{Q}_{p}^{n}\setminus \{0\}$. We show that for the action of a semigroup 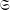$\mathfrak{S}$ of 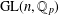$\operatorname{GL}(n,\mathbb{Q}_{p})$ on 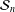${\mathcal{S}}_{n}$, the following are equivalent: (1) 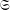$\mathfrak{S}$ acts distally on 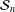${\mathcal{S}}_{n}$; (2) the closure of the image of 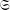$\mathfrak{S}$ in 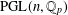$\operatorname{PGL}(n,\mathbb{Q}_{p})$ is a compact group. On 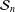${\mathcal{S}}_{n}$, we consider the ‘affine’ maps 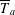$\overline{T}_{a}$ corresponding to 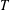$T$ in 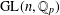$\operatorname{GL}(n,\mathbb{Q}_{p})$ and a nonzero $a$ in 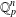$\mathbb{Q}_{p}^{n}$ satisfying 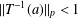$\Vert T^{-1}(a)\Vert _{p}<1$. We show that there exists a compact open subgroup 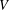$V$, which depends on 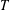$T$, such that 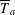$\overline{T}_{a}$ is distal for every nonzero 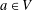$a\in V$ if and only if 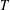$T$ acts distally on 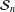${\mathcal{S}}_{n}$. The dynamics of ‘affine’ maps on 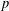$p$-adic unit spheres is quite different from that on the real unit spheres.

Keywords

distal actionsaffine mapsp-adic unit spheres

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 22E35: Analysis on $p$-adic Lie groups
Secondary: 20M20: Semigroups of transformations, etc. 20G25: Linear algebraic groups over local fields and their integers
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 2 , October 2020 , pp. 250 - 261
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

R. Shah would like to acknowledge the support of DST (SERB) through the MATRICS research grant. A. K. Yadav would like to acknowledge the support for a research assistantship from DST-PURSE grant in Jawaharlal Nehru University.

References

Berglund, J. F., Junghenn, H. D. and Milnes, P., Analysis on Semigroups: Function Spaces, Compactifications, Representations, Canadian Mathematical Society Series of Monographs and Advanced Texts (John Wiley & Sons, New York, 1989).Google Scholar
Borel, A. and Tits, J., ‘Groupes réductifs’, Publ. Math. Inst. Hautes Études Sci. 27 (1965), 55–151.Google Scholar
Ellis, R., ‘Distal transformation groups’, Pacific J. Math. 8 (1958), 401–405.Google Scholar
Furstenberg, H., ‘The structure of distal flows’, Amer. J. Math. 85 (1963), 477–515.Google Scholar
Guivarc’h, Y. and Raja, C. R. E., ‘Recurrence and ergodicity of random walks on linear groups and on homogeneous spaces’, Ergodic Theory Dynam. Systems 32 (2012), 1313–1349.Google Scholar
Hofmann, K. H. and Mostert, P. S., Elements of Compact Semigroups (Charles E. Merrill Books, Columbus, OH, 1966).Google Scholar
Koblitz, N., p-Adic Numbers, p-Adic Analysis, and Zeta-Functions, Graduate Texts in Mathematics, 58 (Springer, New York, 1984).Google Scholar
Moore, C. C., ‘Distal affine transformation groups’, Amer. J. Math. 90 (1968), 733–751.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory, Pure and Applied Mathematics, 139 (Academic Press, Boston, 1994). Translated from the 1991 Russian original by Rachel Rowen.Google Scholar
Raja, C. R. E. and Shah, R., ‘Distal actions and shifted convolution property’, Israel J. Math. 177 (2010), 301–318.Google Scholar
Raja, C. R. E. and Shah, R., ‘Some properties of distal actions on locally compact groups’, Ergodic Theory Dynam. Systems 39 (2019), 1340–1360.Google Scholar
Shah, R., ‘Orbits of distal actions on locally compact groups’, J. Lie Theory 22 (2010), 586–599.Google Scholar
Shah, R. and Yadav, A. K., ‘Dynamics of distal actions on unit spheres’, Real Anal. Exchange, to appear.Google Scholar
Wang, J. S. P., ‘The Mautner phenomenon on p-adic Lie groups’, Math. Z. 185 (1984), 403–411.Google Scholar