No CrossRef data available.
Article contents
Disk-like functions
Published online by Cambridge University Press: 09 April 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The class s of functions f(z) which are regular and univalent in the open unit disk △ = {z: |z| < 1} each normalized by the conditions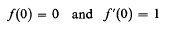
has been studied intensively for over fifty years. A large and very successful portion of this work has dealt with subclasses of L characterized by some geometric property of f[Δ], the image of Δ under f(z), which is expressible in analytic terms. The class of starlike functions in L is one of these [3]; f(z) is starlike with respect to the origin if the segment [0,f(z)] is in f[Δ] for every z in Δ and this condition is equivalent to requiring that 
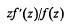have a positive real part in Δ.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1970
References
[1]Jenkins, J. A., ‘On circularly symmetric functions’, Proc. Amer. Math. Soc., 6 (1955), 620–624.CrossRefGoogle Scholar
[2]Kryż, J. and Reade, M. O., ‘Koebe domains for certain classes of analytic functions’, J. d'Analyse Math., 18 (1967), 185–195.CrossRefGoogle Scholar
[4]Robertson, M. S., ‘Analytic functions starlike in one direction’, Amer. J. Math., 58 (1936), 465–472.CrossRefGoogle Scholar
[5]Tammi, O., ‘On certain combinations of the coefficients of schlicht functions’, Ann. Acad. Sci. Fennicae Ser. A. I. Máth.-Phys., No. 140, (1952) 13 pp.,Google Scholar
You have
Access