Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cohn, Harvey
1979.
Number Theory Carbondale 1979.
Vol. 751,
Issue. ,
p.
70.
Schütt, Matthias
Shioda, Tetsuji
and
van Luijk, Ronald
2010.
Lines on Fermat surfaces.
Journal of Number Theory,
Vol. 130,
Issue. 9,
p.
1939.
Schütt, Matthias
2013.
Arithmetic and Geometry of K3 Surfaces and Calabi–Yau Threefolds.
Vol. 67,
Issue. ,
p.
71.
Elkies, Noam D.
and
Schütt, Matthias
2013.
Modular forms and K3 surfaces.
Advances in Mathematics,
Vol. 240,
Issue. ,
p.
106.
Dietmann, Rainer
Fisher, Tom
Smyth, Chris
and
Velani, Sanju
2023.
John William Scott (‘Ian’) Cassels. 11 July 1922—27 July 2015.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 74,
Issue. ,
p.
87.


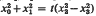 and
and 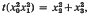 , then
, then 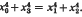 . The proof uses a technique of M. R. Christie.
. The proof uses a technique of M. R. Christie.