Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T13:55:50.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Digit patterns and transcendental numbers

Part of: Elementary number theory

Published online by Cambridge University Press:  09 April 2009

Patrick Morton  and
W. J. Mourant
Patrick Morton
Affiliation:
Wellesley CollegeWellesley, Massachusetts 02181, U.S.A.
W. J. Mourant
Affiliation:
37 William J. Heights Framingham, Massachusetts 01701, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We use a theorem of Loxton and van der Poorten to prove the transcendence of certain real numbers defined by digit patterns. Among the results we prove are the following. If k is an integer at least 2, P is any nonzero pattern of digits base k, and 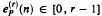counts the number of occurrences (mod r) of p in the base k representation of n, then 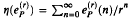is transcendental except when k = 3, P = 1 and r = 2. When (r, k − 1) = 1 the linear span of the numbers 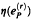has infinite dimension over Q, where P ranges over all patterns base k without leading zeros.

MSC classification

Secondary: 11A63: Radix representation; digital problems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 51 , Issue 2 , October 1991 , pp. 216 - 236
Copyright
Copyright © Australian Mathematical Society 1991

References

[1]Allouche, J. P., ‘Somme de chiffres et transcendance’, Bull. Soc. Math. France 110 (1982), 279–295.CrossRefGoogle Scholar
[2]Allouche, J. P., ‘Automates finis en théorie des nombres’, Expo. Math. 5 (1987), 239–266.Google Scholar
[3]Allouche, J. P. and Shallit, J. O., ‘Infinite products associated with counting blocks in binary strings’, J. London Math. Soc., to appear.Google Scholar
[4]Allouche, J. P. and Shallit, J., ‘The ring of k-regular sequences’, preprint.Google Scholar
[5]Boyd, D. W., Cook, J. and Morton, P., On sequences of ± 1 's defined by binary patterns, Dissertationes Mathematicae 283, Polish Scientific Publishers, Warszawa, 1989.Google Scholar
[6]Christol, G., Kamae, T., France, M. Mendès and Rauzy, G., ‘Suites algébriques, automates et substitutions’, Bull. Soc. Math. France 108 (1980), 401–419.CrossRefGoogle Scholar
[7]Cobham, A., ‘Uniform tag sequences’, Math. Systems Theory 6 (1972), 164–192.CrossRefGoogle Scholar
[8]Dekking, M., France, M. Mendès and van der Poorten, A., ‘Folds! I, II, III’, Math. Intelligencer 4 (1982), 130–138, 173–181, 190–195.Google Scholar
[9]Delange, H., ‘Sur la fonction sommatoire de la fonction ≪somme des chiffres≫’, Enseign. Math. (2) 21 (1975), 31–47.Google Scholar
[10]Loxton, J. H. and van der Poorten, A., ‘Arithmetic properties of the solutions of a class of functional equations’, J. Reine Angew. Math. 330 (1982), 159–172.Google Scholar
[11]Loxton, J. H. and van der Poorten, A. J., ‘Arithmetic properties of automata: regular sequences’, J. Reine Angew. Math. 392 (1988), 57–69.Google Scholar
[12]France, M. Mendès, ‘Nombres algébriques et théorie des automates’, Enseign. Math. (2) 26 (1980), 193–199.Google Scholar
[13]Morton, P. and Mourant, W. J., ‘Paper folding, digit patterns and groups of arithmetic fractals’, Proc. London Math. Soc. (3) 59 (1989), 253–293.CrossRefGoogle Scholar
[14]Morton, P., ‘Connections between binary patterns and paperfolding’, Séminaire de Théorie des Nombres, Bordeaux 2 (1990), 1–12.Google Scholar