Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-29T10:40:19.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Differentiation of composities with respect to a parameter

Published online by Cambridge University Press:  09 April 2009

Alistair Gray
Alistair Gray
Affiliation:
Department of Pure Mathematics, La Trobe University, Victoria, 3083, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A formula is established for differentiating the composite F(ξ)○G(ξ) with respect to the parameter ξ where F and G are maps which assumetheir values in function spaces. This composite is denoted by 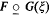. Use of this notation, together with the tangent functor T, enables the formula to be written in the variable-free form 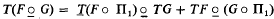where π1 is a projection map and TF(ξ) = T(F(ξ)). Formal verificationof this formula is straightforward. It has application to many small divisor problems such as those which occur in celestial mechanics.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 19 , Issue 1 , February 1975 , pp. 121 - 128
Copyright
Copyright © Australian Mathematical Society 1975

References

Abraham, R. (1967), Foundations of Mechanics (W. A. Benjamin, Inc.; New York, 1967).Google Scholar
Dieudonné, J. (1967), Foundations of Modern Analysis(Academic Press; New York and London; 1960).Google Scholar
Sternberg, Shlomo (1969), Celestial Mechanics, Part II (W. A. Benjamin, Inc.; New York; 1969).Google Scholar