Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T23:10:22.714Z Has data issue: false hasContentIssue false
  • English
  • Français

DIFFERENCES OF COMPOSITION OPERATORS BETWEEN WEIGHTED BANACH SPACES OF HOLOMORPHIC FUNCTIONS

Part of: Special classes of linear operators

Published online by Cambridge University Press:  01 February 2008

JOSÉ BONET ,
MIKAEL LINDSTRÖM  and
ELKE WOLF
JOSÉ BONET*
Affiliation:
Departamento de Matemática Aplicada and IMPA-UPV, Universidad Politécnica de Valencia, E-46071 Valencia, Spain (email: [email protected])
MIKAEL LINDSTRÖM
Affiliation:
Department of Mathematics, Abo Akademi University, FIN-20500 Abo, Finland (email: [email protected])
ELKE WOLF
Affiliation:
Institute of Mathematics, University of Paderborn, D-33095 Paderborn, Germany (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

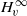We consider differences of composition operators between given weighted Banach spaces or Hv0 of analytic functions with weighted sup-norms and give estimates for the distance of these differences to the space of compact operators. We also study boundedness and compactness of the operators. Some examples illustrate our results.

Keywords

composition operatorsweighted Banach spaces of holomorphic functionscompact operatorsessential norm

MSC classification

Secondary: 47B33: Composition operators 47B38: Operators on function spaces (general)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 1 , February 2008 , pp. 9 - 20
Copyright
Copyright © 2008 Australian Mathematical Society

Footnotes

The research of J. Bonet was partially supported by MEC and FEDER project MTM2004-02262. The work of M. Lindström was partially supported by the Academy of Finland Project 205644.

References

[1]Bierstedt, K. D. and Summers, W. H., ‘Biduals of weighted Banach spaces of analytic functions’, J. Austral. Math. Soc. (Series A) 54 (1993), 70–79.CrossRefGoogle Scholar
[2]Bierstedt, K. D., Bonet, J. and Galbis, A., ‘Weighted spaces of holomorphic functions on bounded domains’, Michigan Math. J. 40 (1993), 271–297.CrossRefGoogle Scholar
[3]Bierstedt, K. D., Bonet, J. and Taskinen, J., ‘Associated weights and spaces of holomorphic functions’, Studia Math. 127 (1998), 137–168.CrossRefGoogle Scholar
[4]Bonet, J., Domański, P. and Lindström, M., ‘Essential norm and weak compactness of composition operators on weighted Banach spaces of analytic functions’, Canad. Math. Bull. 42(2) (1999), 139–148.CrossRefGoogle Scholar
[5]Bonet, J., Domański, P., Lindström, M. and Taskinen, J., ‘Composition operators between weighted Banach spaces of analytic functions’, J. Austral. Math. Soc. (Series A) 64 (1998), 101–118.CrossRefGoogle Scholar
[6]Contreras, M. D. and Hernández-Díaz, A. G., ‘Weighted composition operators in weighted Banach spaces of analytic functions’, J. Austral. Math. Soc. (Series A) 69 (2000), 41–60.CrossRefGoogle Scholar
[7]Cowen, C. and MacCluer, B., Composition operators on spaces of analytc functions (CRC Press, Boca Raton, FL, 1995).Google Scholar
[8]Domański, P. and Lindström, M., ‘Sets of interpolation and sampling for weighted Banach spaces of holomorphic functions’, Ann. Pol. Math. 79(3) (2002), 233–264.CrossRefGoogle Scholar
[9]Garnett, J., Bounded analytic functions (Academic Press, New York, 1981).Google Scholar
[10]Gorkin, P., Mortini, R. and Suárez, D., ‘Homotopic composition operators on ’, Amer. Math. Soc. Contemp. Math. 328 (2003), 177–188.CrossRefGoogle Scholar
[11]Hoffman, K., Banach spaces of analytic functions (Prentice-Hall, Englewood Cliffs, NJ, 1967).Google Scholar
[12]Hosokowa, T. and Izuchi, K., ‘Essential norms of differences of composition operators on ’, J. Math. Soc. Japan 57 (2005), 669–690.Google Scholar
[13]Hosokowa, T., Izuchi, K. and Zheng, D., ‘Isolated points and essential components of composition operators on ’, Proc. Amer. Math. Soc. 130 (2002), 1765–1773.CrossRefGoogle Scholar
[14]Hosokowa, T., Izuchi, K. and Zheng, D., ‘Topological structure of the space of weighted composition operators on ’, Integral Equations Operator Theory 53 (2005), 509–526.CrossRefGoogle Scholar
[15]Jarchow, H., ‘Some functional analytic properties of composition operators’, Quaest. Math. 18 (1995), 229–256.CrossRefGoogle Scholar
[16]Kaballo, W., ‘Lifting-Probleme für -Funktionen’, Arch. Math. 34 (1980), 540–549.CrossRefGoogle Scholar
[17]Lusky, W., ‘On the structure of Hv 0(D) and hv 0(D)’, Math. Nachr. 159 (1992), 279–289.CrossRefGoogle Scholar
[18]Lusky, W., ‘On weighted spaces of harmonic and holomorphic functions’, J. London Math. Soc. 51 (1995), 309–320.CrossRefGoogle Scholar
[19]MacCluer, B., Ohno, S. and Zhao, R., ‘Topological structure of the space of composition operators on ’, Integral Equations Operator Theory 40(4) (2001), 481–494.CrossRefGoogle Scholar
[20]Moorhouse, J., ‘Compact differences of composition operators’, J. Funct. Anal. 219 (2005), 70–92.CrossRefGoogle Scholar
[21]Shapiro, J. H., Composition operators and classical function theory (Springer, New York, 1993).CrossRefGoogle Scholar
[22]Shields, A. L. and Williams, D. L., ‘Bounded projections, duality, and multipliers in spaces of harmonic functions’, J. Reine Angew. Math. 299–300 (1978), 256–279.Google Scholar
[23]Shields, A. L. and Williams, D. L., ‘Bounded projections and the growth of harmonic conjugates in the disc’, Michigan Math. J. 29 (1982), 3–25.CrossRefGoogle Scholar
[24]Wojtaszczyk, P., Banach spaces for analysts, Cambridge Studies in Advanced Mathematics, 25 (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
[25]Wolf, E., ‘Weighted Fréchet spaces of holomorphic functions’, Studia Math. 174 (2006), 255–275.CrossRefGoogle Scholar