No CrossRef data available.
Article contents
The difference of consecutive eigenvalues
Published online by Cambridge University Press: 09 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let M be a smooth bounded domain in Rn with smooth boundary, n ≥ 2, and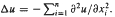 
. We prove an inequality involving the first k + 1 eigenvalues of the eigenvalue problem:
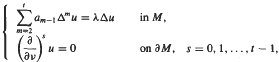where am−1 ≥ 0 are constants and at−1 = 1. We also obtain a uniform estimate of the upper bound of the ratios of consecutive eigenvalues.
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 57 , Issue 3 , December 1994 , pp. 305 - 315
- Copyright
- Copyright © Australian Mathematical Society 1994
References
[1]Chen, Z. C. and Qian, C. L., ‘Estimates for discrete spectrum of Laplace operators with any order’, J. China Univ. Sci. Tech. 20 (1990), 259–266.Google Scholar
[2]Hile, G. N. and Protter, M. H., ‘Inequalities for eigenvalues of the Laplacian’, Indiana Univ. Math. J. 29 (1980), 523–538.CrossRefGoogle Scholar
[3]Hile, G. N. and Yeh, R. Z., ‘Inequalities for eigenvalues of the biharmonic operators’, Pacific J. Math. 112 (1984), 115–133.CrossRefGoogle Scholar
[4]Ku, H. T. and Ku, M. C., Eigenvalue problems for higher order Laplace operators on Riemannian manifolds, mimeographed (University of Massachusetts, Amherst, 1990).Google Scholar
[5]Ku, H. T., Ku, M. C. and Tang, D. Y., ‘Inequalities for eigenvalues of elliptic equations and the generalized Polya conjecture’, J. Differential Equations 97 (1992), 127–139.CrossRefGoogle Scholar
[6]Payne, L. E., Polya, G. and Weinberger, H. F., ‘On the ratio of consecutive eigenvalues’, J. Math. Phys. 35 (1956), 289–298.CrossRefGoogle Scholar
You have
Access