Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-05T17:01:58.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Definitions of integral elements and quotient rings over non-commutative rings with identity

Published online by Cambridge University Press:  09 April 2009

T. W. Atterton
T. W. Atterton
Affiliation:
Department of Pure Mathematics, University of New South Wales
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B be an associative ring with identity, A a subring of B containing the identity of B. If B is commutative then it is customary to define an element b of B to be integral over A if it satisties an equation of the form 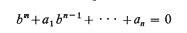for some a1, a2, …, an A. This definition does not generalize readily to the case when B is non-commutative. Van der Waerden ([11], p. 75) defines b ∈ B to be integral over A if all powers of b belong to a finite A-module. This definition is quite satisfactory when A satisfies the ascending chain condition for left ideals, but in the general case this type of integrity is not necessarily transitive, even when B is commutative. Krull [6] calls an element b ∈ B which satisfies the above condition almost integral over A (but he only considers the commutative case). The subset Ā of B consisting of all almost integral elements over A is called the complete integral closure of A in B. If Ā = A, A is said to be completely integrally closed in B. More recently (in [3]), Gilmer and Heinzer (see also Bourbaki, [1]) have discussed these properties in the commutative case and have shown that the complete integral closure of A in B need not be completely integrally closed in B. If B is not commutative, the set A of elements of B almost integral over A, may not even form a ring. In [5] p. 122, Jacobson uses a definition equivalent to Van der Waerden's for the non-commutative case but the definition applies only for a very restricted class of rings.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 13 , Issue 4 , June 1972 , pp. 433 - 446
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Bourbaki, N., Eléments de Mathématique, Algèbre Commutative, XXX (Hermann, Paris, 1964).Google Scholar
[2]Cohen, I. S. and Seidenberg, A., ‘Prime ideals and integral dependence’, Bull. Amer. Math. Soc. 52 (1946), 252–261.CrossRefGoogle Scholar
[3]Gilmer, R. W. and Heinzer, W. J., ‘On the complete integral closure of an integral domain’, J. Australian Math. Soc. 6 (1966), 351–361.CrossRefGoogle Scholar
[4]Jacobson, N., Structure of Rings (Colloquium Publications, number 37, Amer. Math. Soc., 1956).CrossRefGoogle Scholar
[5]Jacobson, N., Theory of Rings (Math. Surveys, number 2, Amer. Math. Soc., New York, 1943).CrossRefGoogle Scholar
[6]Krull, W., ‘Beiträge zur Arithmetik kommutativer Integritätsbereiche II’, Math. Z. 41 (1936), 665–679.CrossRefGoogle Scholar
[7]Lambek, J., Lectures on Rings and Modules (Blaisdell, Mass. 1966).Google Scholar
[8]McCoy, N. H., The Theory of Rings (Macmillan, New York, 1964).Google Scholar
[9]Nagata, M., Local Rings (Interscience, New York, 1962).Google Scholar
[10]Utumi, Y., ‘On Quotient Rings’, Osaka Math. J. 8 (1956), 1–18.Google Scholar
[11]van der Waerden, B. L., Modern Algebra, II (Frederick Ungar, New York, 1950).Google Scholar
[12]Zariski, O. and Samuel, P., Commutotive Algebra, I (Van Nostrand, Princeton, 1962).Google Scholar