Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-29T11:30:37.899Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition theorems for the generalized metaharmonic equation in several independent variables

Published online by Cambridge University Press:  09 April 2009

David Colton
David Colton
Affiliation:
Department of Mathematics McGill UniversityMontreal, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper solutions of the generalized metaharmonic equation in several independent variables 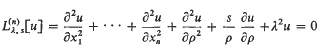where λ > 0 are uniquely decomposed into the sum of a solution regular in the entire space and one satisfying a generalized Sommerfeld radiation condition. Due to the singular nature of the partial differential equation under investigation it is shown that the radiation condition in general must hold uniformly in a domain lying in the space of several complex variables. This result indicates that function theoretic methods are not only the correct and natural avenue of approach in the study of singular ordinary differential equations, but are basic in the investigation of singular partial differential equations as well.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 13 , Issue 1 , February 1972 , pp. 35 - 46
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Colton, D., ‘A Contribution to the Analytic Theory of Partial Differential Equations’, J. Diff. Eqns. 5 (1969), 117–135.CrossRefGoogle Scholar
[2]Colton, D., ‘John's Decomposition Theorem for Generalized Metaharmonic Functions’, J. London Math. Soc. (2), 1 (1969), 737–742.CrossRefGoogle Scholar
[3]Colton, D., ‘Uniqueness Theorems for Axially Symmetric Partial Differential Equations’, J. Math. Mech. 18 (1969), 921–930.Google Scholar
[4]Colton, D., ‘On the Analytic Theory of a Class of Singular Partial Differential Equations’, Proceedings of the Symposium on Analytic Methods in Mathematical Physics, (Gordon and Breach, New York (1970), 415–424.Google Scholar
[5]Colton, D. and Gilbert, R. P., ‘A Contribution to the Vekua-Rellich Theory of Metaharmonic Functions’, American J. Math. (to appear).Google Scholar
[6]Colton, D. and Gilbert, R. P., ‘Function Theoretic Methods in the Theory of Boundary Value Problems for Generalized Metaharmonic Functions’, Bull. Amer. Math. Soc. 75 (1969), 948–952.CrossRefGoogle Scholar
[7]Courant, R. and Hilbert, D., Methods of Mathematical Physics. Vol. II (Wiley, New York (1962)).Google Scholar
[8]Gilbert, R. P., ‘An Invesitgation of the Analytic Properties of Solutions to the Generalized Axially Symmetric Reduced Wave Equation in n+ 1 Variables, with an Application to the Theory of Potential Scattering’, SIAM J. App. Math. 16 (1968), 30–50.CrossRefGoogle Scholar
[9]Gilbert, R. P., Function Theoretic Methods in Partial Differential Equations (Academic Press, New York (1969)).Google Scholar
[10]Erdélyi, A., Higher Transcendental Functions, Vol. II (McGraw-Hill, New York, (1953)).Google Scholar
[11]Erdélyi, A., ‘The Analytic Theory of Systems of Partial Differential Equations’, Bull. Amer. Soc. 57 (1951), 339–353.CrossRefGoogle Scholar
[12]Gunning, R. and Rossi, H., Analytic Functions of Several Complex Variables, (Prentice-Hall, Englewood Cliffs (1965)).Google Scholar
[13]John, F., Recent Developments in the Theory of Wave Propagation, (N.Y.U. Lecture Notes, 1955).Google Scholar
[14]Karp, S., ‘A Convergent ‘Farfield’ Expansion for Two Dimensional Radiation Functions’, Comm. Pure Appl. Math. 14, (1961), 427–434.CrossRefGoogle Scholar