Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Davis, Richard
and
Resnick, Sidney
1988.
Extremes of moving averages of random variables from the domain of attraction of the double exponential distribution.
Stochastic Processes and their Applications,
Vol. 30,
Issue. 1,
p.
41.
Goldie, Charles M.
and
Sidney, Resnick
1988.
Subexponential distribution tails and point processes.
Communications in Statistics. Stochastic Models,
Vol. 4,
Issue. 2,
p.
361.
Goldie, Charles M.
and
Resnick, Sidney
1988.
Distributions that are both subexponential and in the domain of attraction of an extreme-value distribution.
Advances in Applied Probability,
Vol. 20,
Issue. 4,
p.
706.
Goldie, Charles M.
and
Resnick, Sidney
1988.
Distributions that are both subexponential and in the domain of attraction of an extreme-value distribution.
Advances in Applied Probability,
Vol. 20,
Issue. 4,
p.
706.
Klüppelberg, Claudia
1989.
Subexponential distributions and characterizations of related classes.
Probability Theory and Related Fields,
Vol. 82,
Issue. 2,
p.
259.
Leslie, J. R.
1989.
On the non-closure under convolution of the subexponential family.
Journal of Applied Probability,
Vol. 26,
Issue. 1,
p.
58.
Klüppelberg, Claudia
1990.
Asymptotic ordering of distribution functions and convolution semigroups.
Semigroup Forum,
Vol. 40,
Issue. 1,
p.
77.
Cline, Daren B. H.
1990.
Convolutions of distrbutions with exponential and subexponential tails: Corrigendum.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 48,
Issue. 1,
p.
152.
Klüppelberg, Claudia
and
Villasenor, JoséA
1991.
The full solution of the convolution closure problem for convolution-equivalent distributions.
Journal of Mathematical Analysis and Applications,
Vol. 160,
Issue. 1,
p.
79.
Willekens, E.
and
Teugels, J. L.
1992.
Asymptotic expansions for waiting time probabilities in an M/G/1 queue with long-tailed service time.
Queueing Systems,
Vol. 10,
Issue. 4,
p.
295.
Beirlant, Jan
and
Teugels, Jozef L.
1992.
Modeling large claims in non-life insurance.
Insurance: Mathematics and Economics,
Vol. 11,
Issue. 1,
p.
17.
Cline, Daren B.H.
and
Resnick, Sidney I.
1992.
Multivariate subexponential distributions.
Stochastic Processes and their Applications,
Vol. 42,
Issue. 1,
p.
49.
Cline, D.B.H.
and
Samorodnitsky, G.
1994.
Subexponentiality of the product of independent random variables.
Stochastic Processes and their Applications,
Vol. 49,
Issue. 1,
p.
75.
Alzaid, Abdulhamid A.
1994.
Aging concepts for items of unknown age.
Communications in Statistics. Stochastic Models,
Vol. 10,
Issue. 3,
p.
649.
Yakymiv, A. L.
1995.
Sufficient conditions for the subexponential property of the convolution of two distributions.
Mathematical Notes,
Vol. 58,
Issue. 5,
p.
1227.
Braverman, Michael
and
Samorodnitsky, Gennady
1995.
Functionals of infinitely divisible stochastic processes with exponential tails.
Stochastic Processes and their Applications,
Vol. 56,
Issue. 2,
p.
207.
Jelenković, Predrag R.
and
Lazar, Aurel A.
1996.
Stochastic Networks.
Vol. 117,
Issue. ,
p.
215.
Geluk, J.L.
1996.
Tails of subordinated laws: The regularly varying case.
Stochastic Processes and their Applications,
Vol. 61,
Issue. 1,
p.
147.
Samorodnitsky, Gennady
1996.
Athens Conference on Applied Probability and Time Series Analysis.
Vol. 114,
Issue. ,
p.
332.
Yakymiv, A. L.
1997.
Some properties of subexponential distributions.
Mathematical Notes,
Vol. 62,
Issue. 1,
p.
116.
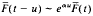 and
and 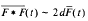 as t → ∞. A real analytic proof is obtained of a theorem by Chover, Wainger and Ney, namely that
as t → ∞. A real analytic proof is obtained of a theorem by Chover, Wainger and Ney, namely that 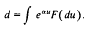 .
.