Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T17:39:07.376Z Has data issue: false hasContentIssue false
  • English
  • Français

CONVOLUTION OPERATORS AND HOMOMORPHISMS OF LOCALLY COMPACT GROUPS

Part of: Abstract harmonic analysis Special classes of linear operators

Published online by Cambridge University Press:  01 June 2008

CÉDRIC DELMONICO
CÉDRIC DELMONICO*
Affiliation:
EPFL SB IACS, Station 8, CH-1015 LAUSANNE, Switzerland (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 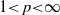, let G and H be locally compact groups and let ω be a continuous homomorphism of G into H. We prove, if G is amenable, the existence of a linear contraction of the Banach algebra CVp(G) of the p-convolution operators on G into CVp(H) which extends the usual definition of the image of a bounded measure by ω. We also discuss the uniqueness of this linear contraction onto important subalgebras of CVp(G). Even if G and H are abelian, we obtain new results. Let Gd denote the group G provided with a discrete topology. As a corollary, we obtain, for every discrete measure, 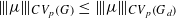, for Gd amenable. For arbitrary G, we also obtain 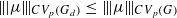. These inequalities were already known for p=2 . The proofs presented in this paper avoid the use of the Hilbertian techniques which are not applicable to 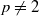. Finally, for Gd amenable, we construct a natural map of CVp (G) into CVp (Gd) .

Keywords

convolution operatorspseudomeasuresp-multiplierstransform theoremHerz algebra

MSC classification

Secondary: 43A22: Homomorphisms and multipliers of function spaces on groups, semigroups, etc. 43A25: Fourier and Fourier-Stieltjes transforms on locally compact and other abelian groups 43A45: Spectral synthesis on groups, semigroups, etc. 47B38: Operators on function spaces (general)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 3 , June 2008 , pp. 329 - 344
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Anker, J.-P., ‘Aspects de la p-induction en analyse harmonique’, PhD Thesis, Université de Lausanne, 1982.Google Scholar
[2]Anker, J.-P., ‘Applications de la p-induction en analyse harmonique’, Comment. Math. Helv. 58(4) (1983), 622–645.CrossRefGoogle Scholar
[3]Bédos, E., ‘On the C *-algebra generated by the left regular representation of a locally compact group’, Proc. Amer. Math. Soc. 120(2) (1994), 603–608.Google Scholar
[4]Bekka, M. B., Kaniuth, E., Lau, A. T. and Schlichting, G., ‘On C *-algebras associated with locally compact groups’, Proc. Amer. Math. Soc. 124(10) (1996), 3151–3158.CrossRefGoogle Scholar
[5]de Leeuw, K., ‘On Lp multipliers’, Ann. of Math. (2) 81 (1965), 364–379.CrossRefGoogle Scholar
[6]Delaporte, J., ‘Convoluteurs continus et topologie stricte’, in: Harmonic Analysis (Luxembourg, 1987) (Springer, Berlin, 1988), pp. 135–141.CrossRefGoogle Scholar
[7]Delaporte, J. and Derighetti, A., ‘p-pseudomeasures and closed subgroups’, Monatsh. Math. 119(1–2) (1995), 37–47.CrossRefGoogle Scholar
[8]Derighetti, A., ‘Relations entre les convoluteurs d’un groupe localement compact et ceux d’un sous-groupe fermé’, Bull. Sci. Math. (2) 106(1) (1982), 69–84.Google Scholar
[9]Derighetti, A., ‘À propos des convoluteurs d’un groupe quotient’, Bull. Sci. Math. (2) 107(1) (1983), 3–23.Google Scholar
[10]Eymard, P., ‘L’algèbre de Fourier d’un groupe localement compact’, Bull. Soc. Math. France 92 (1964), 181–236.CrossRefGoogle Scholar
[11]Herz, C., ‘The theory of p-spaces with an application to convolution operators’, Trans. Amer. Math. Soc. 154 (1971), 69–82.Google Scholar
[12]Herz, C., ‘Harmonic synthesis for subgroups’, Ann. Inst. Fourier (Grenoble) 23(3) (1973), 91–123.CrossRefGoogle Scholar
[13]Herz, C., ‘Une généralisation de la notion de transformée de Fourier–Stieltjes’, Ann. Inst. Fourier (Grenoble) 24(3) (1974), 145–157.CrossRefGoogle Scholar
[14]Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Vol. II: Structure and Analysis for Compact Groups. Analysis on Locally Compact Abelian Groups (Springer, New York, 1970).Google Scholar
[15]Lohoué, N., ‘Sur certains ensembles de synthèse dans les algèbres Ap(G)’, C. R. Acad. Sci. Paris Sér. A–B 270 (1970), A589–A591.Google Scholar
[16]Lohoué, N., ‘Sur le critère de S. Bochner dans les algèbres Bp(Rn) et l’approximation bornée des convoluteurs’, C. R. Acad. Sci. Paris Sér. A–B 271 (1970), A247–A250.Google Scholar
[17]Lohoué, N., ‘Algèbres Ap(G) et convoluteurs de L p(G)’. Doctorat d’état, Université Paris-Sud, Centre d’Orsay, 1971.Google Scholar
[18]Lohoué, N., ‘Approximation et transfert d’opérateurs de convolution’, Ann. Inst. Fourier (Grenoble) 26(4) (1976), 133–150.CrossRefGoogle Scholar
[19]Lust-Piquard, F., ‘Means on CVp(G)-subspaces of CVp(G) with RNP and Schur property’, Ann. Inst. Fourier (Grenoble) 39(4) (1989), 969–1006.CrossRefGoogle Scholar
[20]Pier, J.-P., Amenable Locally Compact Groups (John Wiley & Sons, New York, 1984).Google Scholar
[21]Reiter, H. and Stegeman, J. D., Classical Harmonic Analysis and Locally Compact Groups, 2nd edn (The Clarendon Press/Oxford University Press, New York, 2000).CrossRefGoogle Scholar
[22]Saeki, S., ‘Translation invariant operators on groups’, Tôhoku Math. J. (2) 22 (1970), 409–419.CrossRefGoogle Scholar