Article contents
Convolution, fixed point, and approximation in Stieltjes-Volterra integral equations
Published online by Cambridge University Press: 09 April 2009
Extract
This paper focuses primarily on two aspects of Stieltjes-Volterra integral equation theory. One is a theory for convolution integrals — that is, integrals of the form 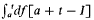 — and the other is a fixed point theorem for a mapping which is induced by an integral equation. Throughout the paper I will denote the identity function whose range of definition should be clear from the context and all integrals will be left integrals, written
— and the other is a fixed point theorem for a mapping which is induced by an integral equation. Throughout the paper I will denote the identity function whose range of definition should be clear from the context and all integrals will be left integrals, written 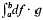 , whose simplest approximating sum is [f(b) – f(a)]·g(a) and whose value is the limit of approximating sums with respect to successive refinements of the interval. Also, N will denote the set of elements of a complete normed ring with unity 1 and S will denote a set linearly ordered by ≦.
, whose simplest approximating sum is [f(b) – f(a)]·g(a) and whose value is the limit of approximating sums with respect to successive refinements of the interval. Also, N will denote the set of elements of a complete normed ring with unity 1 and S will denote a set linearly ordered by ≦.
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 14 , Issue 2 , September 1972 , pp. 182 - 199
- Copyright
- Copyright © Australian Mathematical Society 1972
References
- 3
- Cited by


