Published online by Cambridge University Press: 09 April 2009
It is known that various cases of the steady isentropic irrotational motion of a compressible fluid are expressible as variational principle [1], [5]. in particular, the aerofoil problem i.e. the case of plane flow in which a uniform stream is locally deflected, without circulation, by a bounded obstacle, can be expressed in such a form. Thus we make stationary 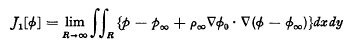 where the region R is that bounded internally by the obstacle (C0) and externally by a circle (CR) of radius R. In this expression φ∞ is the velocity potential for a uniform stream, and φ0 is the velocity potential for the corresponding incompressible flow.
where the region R is that bounded internally by the obstacle (C0) and externally by a circle (CR) of radius R. In this expression φ∞ is the velocity potential for a uniform stream, and φ0 is the velocity potential for the corresponding incompressible flow.