Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T13:35:20.697Z Has data issue: false hasContentIssue false
  • English
  • Français

CONTINUITY OF A CONDITION SPECTRUM AND ITS LEVEL SETS

Part of: Topological algebras, normed rings and algebras, Banach algebras General theory of linear operators

Published online by Cambridge University Press:  09 September 2019

D. SUKUMAR  and
S. VEERAMANI
D. SUKUMAR
Affiliation:
Department of Mathematics, Indian Institute of Technology, Hyderabad, India email [email protected]
S. VEERAMANI*
Affiliation:
Department of Mathematics, School of Advanced Sciences, Vellore Institute of Technology, Vellore, India email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 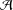${\mathcal{A}}$ be a complex unital Banach algebra, let $a$ be an element in it and let 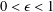$0<\unicode[STIX]{x1D716}<1$. In this article, we study the upper and lower hemicontinuity and joint continuity of the condition spectrum and its level set maps in appropriate settings. We emphasize that the empty interior of the $\unicode[STIX]{x1D716}$-level set of a condition spectrum at a given 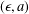$(\unicode[STIX]{x1D716},a)$ plays a pivotal role in the continuity of the required maps at that point. Further, uniform continuity of the condition spectrum map is obtained in the domain of normal matrices.

Keywords

condition spectrumupper and lower hemicontinuous correspondence

MSC classification

Primary: 46H05: General theory of topological algebras
Secondary: 47A10: Spectrum, resolvent
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 3 , June 2020 , pp. 412 - 430
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author thanks the University Grants Commission (UGC), India for the financial support (Ref. no. 23/12/2012(ii)EU-V) provided as a form of Research Fellowship to carry out this research work at IIT Hyderabad.

References

Aliprantis, C. D. and Border, K. C., Infinite Dimensional Analysis, 3rd edn (Springer, Berlin, 2006).Google Scholar
Aubin, J.-P. and Frankowska, H., Set-Valued Analysis, reprint of the 1990 edition, Modern Birkhäuser Classics (Birkhäuser, Boston, MA, 2009).Google Scholar
Bhatia, R., Notes on Functional Analysis, Texts and Readings in Mathematics, 50 (Hindustan Book Agency, New Delhi, 2009).Google Scholar
Burlando, L., ‘Continuity of spectrum and spectral radius in Banach algebras’, in: Functional Analysis and Operator Theory (Warsaw, 1992), Banach Center Publications, 30 (Institute of Mathematics Polish Academy of Sciences, Warsaw, 1994), 53–100.Google Scholar
Globevnik, J., ‘Norm-constant analytic functions and equivalent norms’, Illinois J. Math. 20(3) (1976), 503–506.Google Scholar
Horn, R. A. and Johnson, C. R., Matrix Analysis, 2nd edn (Cambridge University Press, Cambridge, 2013).Google Scholar
Krishnan, A. and Kulkarni, S. H., ‘Pseudospectrum of an element of a Banach algebra’, Oper. Matrices 11(1) (2017), 263–287.Google Scholar
Kulkarni, S. H. and Sukumar, D., ‘The condition spectrum’, Acta Sci. Math. (Szeged) 74(3–4) (2008), 625–641.Google Scholar
Newburgh, J. D., ‘The variation of spectra’, Duke Math. J. 18 (1951), 165–176.Google Scholar
Rickart, C. E., General Theory of Banach Algebras, The University Series in Higher Mathematics (van Nostrand, Princeton, NJ, 1960).Google Scholar
Shargorodsky, E., ‘On the level sets of the resolvent norm of a linear operator’, Bull. Lond. Math. Soc. 40(3) (2008), 493–504.Google Scholar
Shargorodsky, E., ‘On the definition of pseudospectra’, Bull. Lond. Math. Soc. 41(3) (2009), 524–534.Google Scholar
Sukumar, D. and Veeramani, S., ‘Level sets of the condition spectrum’, Ann. Funct. Anal. 8(3) (2017), 314–328.Google Scholar