Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-25T20:09:06.657Z Has data issue: false hasContentIssue false
  • English
  • Français

CONTACT METRIC THREE-MANIFOLDS WITH CONSTANT SCALAR TORSION

Part of: Global differential geometry Symplectic geometry, contact geometry

Published online by Cambridge University Press:  29 October 2018

T. KOUFOGIORGOS  and
C. TSICHLIAS
T. KOUFOGIORGOS*
Affiliation:
University of Ioannina, Department of Mathematics, Ioannina 45110, Greece email [email protected]
C. TSICHLIAS
Affiliation:
University of the Aegean, Department of Mathematics, Karlovassi 83200, Samos, Greece email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study three-dimensional contact metric manifolds satisfying 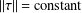$\Vert \unicode[STIX]{x1D70F}\Vert =\text{constant}$. The local description, as well as several global results and new examples of such manifolds are given.

Keywords

contact metric manifoldsscalar torsionJacobi operator

MSC classification

Primary: 53D10: Contact manifolds, general 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.)
Secondary: 53C15: General geometric structures on manifolds (almost complex, almost product structures, etc.)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 2 , October 2019 , pp. 234 - 255
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Blair, D. E., Riemannian Geometry of Contact and Symplectic Manifolds, 2nd edn, Progress in Mathematics, 203 (Birkhäuser, Boston, 2010).Google Scholar
Blair, D. E., Koufogiorgos, T. and Papantoniou, B., ‘Contact metric manifolds satisfying a nullity condition’, Israel J. Math. 91 (1995), 189–214.Google Scholar
Calvaruso, G., Perrone, D. and Vanhecke, L., ‘Homogeneity on three-dimensional contact metric manifolds’, Israel J. Math. 114 (1999), 301–321.Google Scholar
Chern, S. S. and Hamilton, R. S., On Riemannian Metrics Adapted to Three-Dimensional Contact Manifolds, Lecture Notes in Mathematics, 1111 (Springer, Berlin, 1985), 279–305.Google Scholar
Ghosh, A. and Sharma, R., ‘A generalization of K-contact and (𝜅, 𝜇)-contact manifolds’, J. Geom. 103(3) (2012), 431–443.Google Scholar
Gouli-Andreou, F. and Moutafi, E., ‘Two classes of pseudosymmetric contact metric 3-manifolds’, Pacific J. Math. 239(1) (2009), 17–37.Google Scholar
Gouli-Andreou, F. and Moutafi, E., ‘Three classes of pseudosymmetric contact metric 3-manifolds’, Pacific J. Math. 245(1) (2010), 57–77.Google Scholar
Gouli-Andreou, F. and Xenos, P., ‘On 3-dimensional contact metric manifolds with 𝛻𝜉𝜏 = 0’, J. Geom. 62 (1998), 154–165.Google Scholar
Koufogiorgos, T., Markellos, M. and Tsichlias, C., ‘Tangent sphere bundles with constant trace of the Jacobi operator’, Beitr. Algebra Geom. 53(2) (2012), 551–568.Google Scholar
Koufogiorgos, T. and Tsichlias, C., ‘On the existence of a new class of contact metric manifolds’, Canad. Math. Bull. 43 (2000), 440–447.Google Scholar
Koufogiorgos, T. and Tsichlias, C., ‘Three dimensional contact metric manifolds with vanishing Jacobi operator’, Beitr. Algebra Geom. 50(2) (2009), 563–573.Google Scholar
Perrone, D., ‘Homogeneous contact Riemannian three-manifolds’, Illinois J. Math. 42(2) (1998), 243–256.Google Scholar
Perrone, D., ‘Contact metric manifolds whose characteristic vector field is a harmonic vector field’, Differential Geom. Appl. 20(3) (2004), 367–378.Google Scholar
Tanno, S., ‘The topology of contact Riemannian manifolds’, Illinois J. Math. 12 (1968), 700–717.Google Scholar