Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-11T10:01:10.348Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruence networks for completely simple semigroups

Part of: Semigroups

Published online by Cambridge University Press:  09 April 2009

Mario Petrich
Mario Petrich
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, B.C. V5A156, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The operators K, k, T and t are defined on the lattice 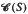of congruences on a Rees matrix semigroup S as follows. For ρ ∈ 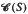(S), ρK and ρk (ρT and ρt) are the greatest and the least congruences with the same kernel (trace) as ρ, respectively. We determine the semigroup generated by the operators K, k, T and t as they act on all completely simple semigroups. We also determine the network of congruences associated with a congruence ρ ∈ 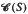(S) and the lattice generated by it. The latter is then represented by generators and relations.

MSC classification

Secondary: 20M10: General structure theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 56 , Issue 2 , April 1994 , pp. 243 - 266
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Howie, J. M., An introduction to semigroup theory (Academic Press, London, 1976).Google Scholar
[2]Pastijn, F. and Petrich, M., ‘Congruences on a regular semigroup’, Trans. Amer. Math. Soc. 295 (1986), 607–633.CrossRefGoogle Scholar
[3]Pastijn, F. and Trotter, P. G., ‘Lattices of completely regular semigroup varieties’, Pacific J. Math 119 (1985), 191–214.CrossRefGoogle Scholar
[4]Petrich, M., ‘A special sublattice of the congruence lattice of a regular semigroup’, preprint.CrossRefGoogle Scholar
[5]Petrich, M., ‘Congruence lattices of regular semigroups related to kernels and traces’, Proc. Edinburgh Math. Soc. 34 (1991), 179–203.CrossRefGoogle Scholar
[6]Petrich, M. and Reilly, N. R., ‘The kernel-trace approach to congruences on completely simple semigroups’, Studia Sci. Math. Hungar. 16 (1981), 103–114.Google Scholar
[7]Petrich, M. and Reilly, N. R., ‘A network of congruences on an inverse semigroup’, Trans. Amer. Math. Soc. 270 (1982), 309–325.CrossRefGoogle Scholar
[8]Petrich, M. and Reilly, N. R., ‘Semigroups generated by certain operators on varieties of completely regular semigroups’, Pacific J. Math. 132 (1988), 151–175.CrossRefGoogle Scholar