Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T14:25:49.180Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPLEX NUMBERS WITH BOUNDED PARTIAL QUOTIENTS

Part of: Elementary number theory

Published online by Cambridge University Press:  16 April 2013

WIEB BOSMA  and
DAVID GRUENEWALD
WIEB BOSMA*
Affiliation:
Department of Mathematics, Radboud Universiteit, PO Box 9010, 6500 GL Nijmegen, The Netherlands
DAVID GRUENEWALD
Affiliation:
Laboratoire de Mathématiques Nicolas Oresme, CNRS—UMR 6139, Université de Caen Basse-Normandie, Boulevard Maréchal Juin, BP 5186, 14032 Caen cedex, France email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Conjecturally, the only real algebraic numbers with bounded partial quotients in their regular continued fraction expansion are rationals and quadratic irrationals. We show that the corresponding statement is not true for complex algebraic numbers in a very strong sense, by constructing, for every even degree 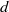$d$, algebraic numbers of degree 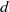$d$ that have bounded complex partial quotients in their Hurwitz continued fraction expansion. The Hurwitz expansion is the complex generalization of the nearest integer continued fraction for real numbers. In the case of real numbers the boundedness of regular and nearest integer partial quotients is equivalent.

Keywords

continued fractionbounded partial quotientsalgebraic numbers

MSC classification

Secondary: 11A55: Continued fractions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 93 , Issue 1-2 , October 2012 , pp. 9 - 20
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc.

References

Hensley, D., ‘Complex continued fractions’, in: Continued Fractions (World Scientific, Singapore, 2006), Ch. 5.CrossRefGoogle Scholar
Hurwitz, A., ‘Über die Entwicklung complexer Grössen in Kettenbrüche’, Acta Math. 11 (1888), 187–200.CrossRefGoogle Scholar
Hurwitz, J., ‘Über die Reduction der binären quadratischen Formen mit complexen Coëfficiënten und Variabeln’, Acta Math. 25 (1901), 231–290.CrossRefGoogle Scholar
Schmidt, A., ‘Diophantine approximation of complex numbers’, Acta Math. 134 (1975), 1–85.CrossRefGoogle Scholar
Shallit, J. O., ‘Real numbers with bounded partial quotients. A survey’, Enseign. Math. 38 (1992), 151–187.Google Scholar