Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-22T23:13:32.984Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact Semirings Which are Multiplicatively 0-Simple1

Published online by Cambridge University Press:  09 April 2009

K. R. Pearson
K. R. Pearson
Affiliation:
The University of Adelaide South Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A topological semiring is a system (S, +, ⋅) where (S, +) and (S, ⋅) are topological semigroups and the distributive laws 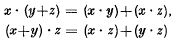, hold for all x, y, z in S; + and ⋅ are called addition and multiplication respectively.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 10 , Issue 3-4 , November 1969 , pp. 320 - 329
Copyright
Copyright © Australian Mathematical Society 1969

References

[1]Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. I (Amer. Math. Soc., 1961).Google Scholar
[2]Koch, R. J. and Wallace, A. D., ‘Maximal ideals in compact semigroups’, Duke Math. J. 21 (1954), 681–685.CrossRefGoogle Scholar
[3]Miranda, A. B. Paalman-de, Topological semigroups (Mathematisch Centrum, Amsterdam, 1964).Google Scholar
[4]Pearson, K. R., ‘Compact semirings which are multiplicatively groups or groups with zero’, Math. Zeitschr. 106 (1968), 388–394.CrossRefGoogle Scholar
[5]Pearson, K. R., ‘The three kernels of a compact semiring’, J. Australian Math. Soc. 10 (1969), 299–319.CrossRefGoogle Scholar
[6]Selden, J., Theorems on topological semigroups and semirings (Doctoral Dissertation, University of Georgia, 1963).Google Scholar
[7]Selden, J., ‘Left zero simplicity in semirings’, Proc. Amer. Math. Soc. 17 (1966), 694–698.Google Scholar
[8]Wallace, A. D., ‘Cohomology, dimension and mobs’, Summa Brasil. Math. 3 (1953), 43–54.Google Scholar
[9]Wallace, A. D., ‘The Rees-Suschkewitsch structure theorem for compact simple semigroups’, Proc. Nat. Acad. Sci. 42 (1956), 430–432.CrossRefGoogle ScholarPubMed
[10]Zassenhaus, H., The theory of groups (Chelsea, New York, 1949).Google Scholar