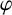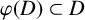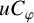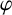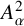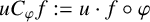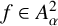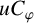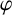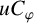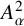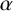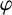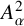1 Introduction
Let D be the unit disk
![]() $\{z \in {\mathbb C} : |z| < 1\}$
in the complex plane
$\{z \in {\mathbb C} : |z| < 1\}$
in the complex plane
![]() ${\mathbb C}$
and T be the unit circle
${\mathbb C}$
and T be the unit circle
![]() $\{z \in {\mathbb C} : |z| = 1\}$
. For
$\{z \in {\mathbb C} : |z| = 1\}$
. For
![]() $0 < p < \infty $
and
$0 < p < \infty $
and
![]() $\alpha> -1$
, the weighted Bergman space
$\alpha> -1$
, the weighted Bergman space
![]() $A^p_{\alpha }$
of D consists of all analytic functions f in
$A^p_{\alpha }$
of D consists of all analytic functions f in
![]() $L^p(D, dA_{\alpha })$
, that is,
$L^p(D, dA_{\alpha })$
, that is,
where
![]() $dA_{\alpha }(z) := (\alpha + 1)(1 - |z|^2)^{\alpha } dA(z)$
and
$dA_{\alpha }(z) := (\alpha + 1)(1 - |z|^2)^{\alpha } dA(z)$
and
![]() $dA(z) := ({1}/{\pi })\,dx\,dy$
is the normalized area measure on D. It is known that
$dA(z) := ({1}/{\pi })\,dx\,dy$
is the normalized area measure on D. It is known that
![]() $A^2_{\alpha }$
is a closed subspace of
$A^2_{\alpha }$
is a closed subspace of
![]() $L^2(D, dA_{\alpha })$
and is thus a Hilbert space with the inner product
$L^2(D, dA_{\alpha })$
and is thus a Hilbert space with the inner product
![]() $\langle \cdot ,\cdot \rangle $
given by
$\langle \cdot ,\cdot \rangle $
given by
In what follows, we denote the norm on
![]() $A^2_{\alpha }$
by
$A^2_{\alpha }$
by
![]() $\|\cdot \|$
for brevity. By writing
$\|\cdot \|$
for brevity. By writing
![]() $f(z) = \sum _{k = 0}^{\infty } a_k z^k$
, we have
$f(z) = \sum _{k = 0}^{\infty } a_k z^k$
, we have
 $$ \begin{align*}\|f\|^2 = \sum_{k = 0}^{\infty} \frac{k! \, \Gamma(\alpha + 2)}{\Gamma(\alpha + 2 + k)}|a_k|^2, \end{align*} $$
$$ \begin{align*}\|f\|^2 = \sum_{k = 0}^{\infty} \frac{k! \, \Gamma(\alpha + 2)}{\Gamma(\alpha + 2 + k)}|a_k|^2, \end{align*} $$
where
![]() $\Gamma $
is the usual gamma function. If we let
$\Gamma $
is the usual gamma function. If we let
 $$ \begin{align} e_k(z) = \sqrt{\frac{\Gamma(\alpha + 2 + k)}{k!\,\Gamma(\alpha + 2)}}\, z^k \quad {\textrm{for}} \ k = 0, 1, \ldots, \end{align} $$
$$ \begin{align} e_k(z) = \sqrt{\frac{\Gamma(\alpha + 2 + k)}{k!\,\Gamma(\alpha + 2)}}\, z^k \quad {\textrm{for}} \ k = 0, 1, \ldots, \end{align} $$
then
![]() $\{e_k\}_{k=0}^{\infty }$
is the standard orthonormal basis for
$\{e_k\}_{k=0}^{\infty }$
is the standard orthonormal basis for
![]() $A^2_{\alpha }$
. Furthermore, if w is an arbitrary point in D, then
$A^2_{\alpha }$
. Furthermore, if w is an arbitrary point in D, then
![]() $\langle f, k_w\rangle = f(w)$
for all
$\langle f, k_w\rangle = f(w)$
for all
![]() $f \in A^2_{\alpha }$
, where
$f \in A^2_{\alpha }$
, where
![]() $k_w(z) := 1/(1 - \overline {w}z)^{\alpha + 2}$
is the reproducing kernel representing the point evaluation functional on
$k_w(z) := 1/(1 - \overline {w}z)^{\alpha + 2}$
is the reproducing kernel representing the point evaluation functional on
![]() $A^2_{\alpha }$
at
$A^2_{\alpha }$
at
![]() $z = w$
. Moreover,
$z = w$
. Moreover,
![]() $\|k_w\|^2 = 1/(1 - |w|^2)^{\alpha + 2}$
.
$\|k_w\|^2 = 1/(1 - |w|^2)^{\alpha + 2}$
.
Let u and
![]() $\varphi $
be two analytic functions on D such that
$\varphi $
be two analytic functions on D such that
![]() $\varphi (D) \subset D$
. They induce a weighted composition operator
$\varphi (D) \subset D$
. They induce a weighted composition operator
![]() $uC_{\varphi }$
from
$uC_{\varphi }$
from
![]() $A^2_{\alpha }$
into the linear space of all analytic functions on D by
$A^2_{\alpha }$
into the linear space of all analytic functions on D by
When
![]() $u \equiv 1$
, the corresponding operator, denoted by
$u \equiv 1$
, the corresponding operator, denoted by
![]() $C_{\varphi }$
, is known as a composition operator. From exercise 3.1.3 in [Reference Cowen and MacCluer3, page 127],
$C_{\varphi }$
, is known as a composition operator. From exercise 3.1.3 in [Reference Cowen and MacCluer3, page 127],
![]() $C_{\varphi }$
is always bounded. However, this is not necessarily true for weighted composition operators. When
$C_{\varphi }$
is always bounded. However, this is not necessarily true for weighted composition operators. When
![]() $uC_{\varphi }$
maps
$uC_{\varphi }$
maps
![]() $A^2_{\alpha }$
into itself, we say
$A^2_{\alpha }$
into itself, we say
![]() $uC_{\varphi }$
is a weighted composition operator on
$uC_{\varphi }$
is a weighted composition operator on
![]() $A^2_{\alpha }$
. In this case,
$A^2_{\alpha }$
. In this case,
![]() $u = uC_{\varphi }1 \in A^2_{\alpha }$
. An appeal to the closed graph theorem shows that every operator
$u = uC_{\varphi }1 \in A^2_{\alpha }$
. An appeal to the closed graph theorem shows that every operator
![]() $uC_{\varphi }$
on
$uC_{\varphi }$
on
![]() $A^2_{\alpha }$
is bounded. Furthermore, if
$A^2_{\alpha }$
is bounded. Furthermore, if
![]() $g \in A^2_{\alpha }$
and
$g \in A^2_{\alpha }$
and
![]() $w \in D$
, then
$w \in D$
, then
Thus,
During the past two decades, several authors have studied the properties of (weighted) composition operators on
![]() $A^p_{\alpha }$
with Berezin transforms and Carleson-type measures (see for example [Reference Čučković and Zhao4, Reference Čučković and Zhao5, Reference MacCluer and Shapiro11, Reference Mirzakarimi and Seddighi13]). In Section 2, we obtain sufficient conditions for the compactness of
$A^p_{\alpha }$
with Berezin transforms and Carleson-type measures (see for example [Reference Čučković and Zhao4, Reference Čučković and Zhao5, Reference MacCluer and Shapiro11, Reference Mirzakarimi and Seddighi13]). In Section 2, we obtain sufficient conditions for the compactness of
![]() $uC_{\varphi }$
in terms of function-theoretic properties of u and
$uC_{\varphi }$
in terms of function-theoretic properties of u and
![]() $\varphi $
. In Section 3, we characterize Hilbert–Schmidt weighted composition operators and the Hilbert–Schmidt difference of two weighted composition operators on
$\varphi $
. In Section 3, we characterize Hilbert–Schmidt weighted composition operators and the Hilbert–Schmidt difference of two weighted composition operators on
![]() $A^2_{\alpha }$
.
$A^2_{\alpha }$
.
2 Compact weighted composition operators
A bounded linear operator T from a Banach space
![]() $B_1$
to a Banach space
$B_1$
to a Banach space
![]() $B_2$
is said to be compact if it maps bounded subsets of
$B_2$
is said to be compact if it maps bounded subsets of
![]() $B_1$
into relatively compact subsets of
$B_1$
into relatively compact subsets of
![]() $B_2$
. Equivalently, T is compact if and only if it maps every bounded sequence
$B_2$
. Equivalently, T is compact if and only if it maps every bounded sequence
![]() $\{x_n\}_{n = 1}^{\infty }$
in
$\{x_n\}_{n = 1}^{\infty }$
in
![]() $B_1$
onto a sequence
$B_1$
onto a sequence
![]() $\{Tx_n\}_{n = 1}^{\infty }$
in
$\{Tx_n\}_{n = 1}^{\infty }$
in
![]() $B_2$
which has a convergent subsequence. It was shown in [Reference Mirzakarimi and Seddighi13, Theorem 4.3] that
$B_2$
which has a convergent subsequence. It was shown in [Reference Mirzakarimi and Seddighi13, Theorem 4.3] that
![]() $uC_{\varphi }$
is compact on
$uC_{\varphi }$
is compact on
![]() $A^p_{\alpha }$
if and only if
$A^p_{\alpha }$
if and only if
 $$ \begin{align*}\lim_{\delta \to 0^+} \sup_{\zeta \in T} \frac{\mu_{\alpha,\, p} \circ \varphi^{-1}(S(\zeta, \delta))}{\delta^{\alpha + 2}} = 0, \end{align*} $$
$$ \begin{align*}\lim_{\delta \to 0^+} \sup_{\zeta \in T} \frac{\mu_{\alpha,\, p} \circ \varphi^{-1}(S(\zeta, \delta))}{\delta^{\alpha + 2}} = 0, \end{align*} $$
where
![]() $S(\zeta , \delta ) := \{z \in D : |z - \zeta | < \delta \}$
and
$S(\zeta , \delta ) := \{z \in D : |z - \zeta | < \delta \}$
and
![]() $\mu _{\alpha ,\, p} \circ \varphi ^{-1}$
is the measure such that
$\mu _{\alpha ,\, p} \circ \varphi ^{-1}$
is the measure such that
![]() $\|uC_{\varphi }f\|_{A^p_{\alpha }}^p = \int _D |f|^p d\mu _{\alpha ,\, p} \circ \varphi ^{-1}$
for all
$\|uC_{\varphi }f\|_{A^p_{\alpha }}^p = \int _D |f|^p d\mu _{\alpha ,\, p} \circ \varphi ^{-1}$
for all
![]() $f \in A^p_{\alpha }$
. Later, Čučković and Zhao estimated the essential norm of
$f \in A^p_{\alpha }$
. Later, Čučković and Zhao estimated the essential norm of
![]() $uC_{\varphi }$
and deduced that
$uC_{\varphi }$
and deduced that
![]() $uC_{\varphi }$
is compact on
$uC_{\varphi }$
is compact on
![]() $A^2_0$
if and only if
$A^2_0$
if and only if
 $$ \begin{align*}\lim_{|a| \to 1^-} \int_D \frac{(1 - |a|^2)^2 |u(z)|^2}{|1 - \overline{a}\varphi(z)|^4} \, dA(z) = 0 \end{align*} $$
$$ \begin{align*}\lim_{|a| \to 1^-} \int_D \frac{(1 - |a|^2)^2 |u(z)|^2}{|1 - \overline{a}\varphi(z)|^4} \, dA(z) = 0 \end{align*} $$
[Reference Čučković and Zhao4, Corollary 2]. These characterizations, however, are rather implicit and less tractable. In this section, we provide more explicit sufficient conditions that guarantee
![]() $uC_{\varphi }$
is compact on
$uC_{\varphi }$
is compact on
![]() $A^2_{\alpha }$
. To this end, we first state a useful result to the study of compact weighted composition operators on
$A^2_{\alpha }$
. To this end, we first state a useful result to the study of compact weighted composition operators on
![]() $A^2_{\alpha }$
.
$A^2_{\alpha }$
.
Lemma 2.1. Let
![]() $uC_{\varphi }$
be a weighted composition operator on
$uC_{\varphi }$
be a weighted composition operator on
![]() $A^2_{\alpha }$
. The following two statements are equivalent:
$A^2_{\alpha }$
. The following two statements are equivalent:
-
(i)
 $uC_{\varphi }$
is compact on
$uC_{\varphi }$
is compact on
 $A^2_{\alpha }$
;
$A^2_{\alpha }$
; -
(ii) if
 $\{f_n\}_{n = 1}^{\infty }$
is a bounded sequence in
$\{f_n\}_{n = 1}^{\infty }$
is a bounded sequence in
 $A^2_{\alpha }$
and
$A^2_{\alpha }$
and
 $f_n \to 0$
uniformly on compact subsets of D, then
$f_n \to 0$
uniformly on compact subsets of D, then
 $\|uC_{\varphi }f_n\| \to 0$
.
$\|uC_{\varphi }f_n\| \to 0$
.
While the above lemma is a generalization of [Reference Cowen and MacCluer3, Proposition 3.11], it can also be obtained by a Hilbert space argument. From exercise 4.7.1 in [Reference Zhu17, page 97], a sequence of functions in
![]() $A^2_{\alpha }$
is weakly convergent to zero if and only if this sequence is norm bounded and converges to zero uniformly on compact subsets of D. Lemma 2.1 now follows from this fact and [Reference Zhu17, Theorem 1.14].
$A^2_{\alpha }$
is weakly convergent to zero if and only if this sequence is norm bounded and converges to zero uniformly on compact subsets of D. Lemma 2.1 now follows from this fact and [Reference Zhu17, Theorem 1.14].
One simple sufficient condition for the compactness of
![]() $uC_{\varphi }$
, which is analogous to [Reference Gunatillake7, Theorem 2], is given below.
$uC_{\varphi }$
, which is analogous to [Reference Gunatillake7, Theorem 2], is given below.
Theorem 2.2. Suppose that
![]() $uC_{\varphi }$
is a weighted composition operator on
$uC_{\varphi }$
is a weighted composition operator on
![]() $A^2_{\alpha }$
. If
$A^2_{\alpha }$
. If
![]() $\overline {\varphi (D)} \subset D$
, then
$\overline {\varphi (D)} \subset D$
, then
![]() $uC_{\varphi }$
is compact.
$uC_{\varphi }$
is compact.
Proof. Since
![]() $\overline {\varphi (D)} \subset D$
, there is a constant M such that
$\overline {\varphi (D)} \subset D$
, there is a constant M such that
![]() $0 < M < 1$
and
$0 < M < 1$
and
![]() $|\varphi (z)| \leq M$
for all
$|\varphi (z)| \leq M$
for all
![]() $z \in D$
. Let
$z \in D$
. Let
![]() $\{f_n\}_{n = 1}^{\infty }$
be a bounded sequence in
$\{f_n\}_{n = 1}^{\infty }$
be a bounded sequence in
![]() $A^2_{\alpha }$
such that
$A^2_{\alpha }$
such that
![]() $f_n \to 0$
uniformly on compact subsets of D. In particular, this sequence converges to zero uniformly on
$f_n \to 0$
uniformly on compact subsets of D. In particular, this sequence converges to zero uniformly on
![]() $\overline {S(0, M)}$
. Then there exists some
$\overline {S(0, M)}$
. Then there exists some
![]() $N \in {\mathbb N}$
for which
$N \in {\mathbb N}$
for which
![]() $|f_n(\varphi (z))| < \epsilon $
whenever
$|f_n(\varphi (z))| < \epsilon $
whenever
![]() $n> N$
and
$n> N$
and
![]() $z \in D$
. With
$z \in D$
. With
![]() $u \in A^2_{\alpha }$
, it follows that
$u \in A^2_{\alpha }$
, it follows that
![]() $\|uC_{\varphi } f_n\| \leq \epsilon \|u\|$
for all
$\|uC_{\varphi } f_n\| \leq \epsilon \|u\|$
for all
![]() $n> N$
. By Lemma 2.1,
$n> N$
. By Lemma 2.1,
![]() $uC_{\varphi }$
is compact.
$uC_{\varphi }$
is compact.
We remark that the condition
![]() $\overline {\varphi (D)} \subset D$
in Theorem 2.2 is sufficient, but not necessary for the compactness of
$\overline {\varphi (D)} \subset D$
in Theorem 2.2 is sufficient, but not necessary for the compactness of
![]() $uC_{\varphi }$
. This is shown below.
$uC_{\varphi }$
. This is shown below.
Example 2.3. Let
![]() $u(z) = z-1$
and
$u(z) = z-1$
and
![]() $\varphi (z) = (z + 1) / 2$
. Note that
$\varphi (z) = (z + 1) / 2$
. Note that
![]() $1 \in \overline {\varphi (D)}$
. Choose any
$1 \in \overline {\varphi (D)}$
. Choose any
![]() $\varepsilon> 0$
. With
$\varepsilon> 0$
. With
![]() $u(1) = 0$
and the continuity of u at
$u(1) = 0$
and the continuity of u at
![]() $z = 1$
, there is a sufficiently small
$z = 1$
, there is a sufficiently small
![]() $\delta> 0$
such that
$\delta> 0$
such that
![]() $|u|^2 < \varepsilon $
on
$|u|^2 < \varepsilon $
on
![]() $S(1, \delta )$
. We show that
$S(1, \delta )$
. We show that
![]() $uC_{\varphi }$
is compact by using Lemma 2.1.
$uC_{\varphi }$
is compact by using Lemma 2.1.
Let
![]() $\{f_n\}_{n = 1}^{\infty }$
be a sequence in
$\{f_n\}_{n = 1}^{\infty }$
be a sequence in
![]() $A^2_{\alpha }$
such that
$A^2_{\alpha }$
such that
![]() $\|f_n\| \leq 1$
for all
$\|f_n\| \leq 1$
for all
![]() $n \in {\mathbb N}$
and
$n \in {\mathbb N}$
and
![]() $f_n \to 0$
uniformly on compact subsets of D. Since
$f_n \to 0$
uniformly on compact subsets of D. Since
![]() $\varphi $
is continuous on the compact set
$\varphi $
is continuous on the compact set
![]() $\overline {D \setminus S(1, \delta )}$
, the set
$\overline {D \setminus S(1, \delta )}$
, the set
![]() $\varphi (\overline {D \setminus S(1, \delta )})$
is compact in D. Then there exists some
$\varphi (\overline {D \setminus S(1, \delta )})$
is compact in D. Then there exists some
![]() $N \in {\mathbb N}$
for which if
$N \in {\mathbb N}$
for which if
![]() $n> N$
and
$n> N$
and
![]() $z \in D \setminus S(1, \delta )$
, we have
$z \in D \setminus S(1, \delta )$
, we have
These, together with the fact that
![]() $C_{\varphi }$
is bounded on
$C_{\varphi }$
is bounded on
![]() $A^2_{\alpha }$
, imply
$A^2_{\alpha }$
, imply
 $$ \begin{align*} \|uC_{\varphi} f_n\|^2 & = \int_{S(1, \delta)} |u(z)|^2 |f_n(\varphi(z))|^2\, dA_{\alpha}(z) + \int_{D \setminus S(1, \delta)} |u(z)|^2 |f_n(\varphi(z))|^2\, dA_{\alpha}(z) \\[3pt] & \leq \varepsilon\int_{S(1, \delta)} |f_n(\varphi(z))|^2\, dA_{\alpha}(z) + \varepsilon\int_{D \setminus S(1, \delta)} |u(z)|^2\, dA_{\alpha}(z) \\[3pt] & \leq \varepsilon \|C_{\varphi} f_n\|^2 + \varepsilon \int_D |u(z)|^2\, dA_{\alpha}(z) \\[3pt] & \leq (\|C_{\varphi}\|^2 + 4)\varepsilon \end{align*} $$
$$ \begin{align*} \|uC_{\varphi} f_n\|^2 & = \int_{S(1, \delta)} |u(z)|^2 |f_n(\varphi(z))|^2\, dA_{\alpha}(z) + \int_{D \setminus S(1, \delta)} |u(z)|^2 |f_n(\varphi(z))|^2\, dA_{\alpha}(z) \\[3pt] & \leq \varepsilon\int_{S(1, \delta)} |f_n(\varphi(z))|^2\, dA_{\alpha}(z) + \varepsilon\int_{D \setminus S(1, \delta)} |u(z)|^2\, dA_{\alpha}(z) \\[3pt] & \leq \varepsilon \|C_{\varphi} f_n\|^2 + \varepsilon \int_D |u(z)|^2\, dA_{\alpha}(z) \\[3pt] & \leq (\|C_{\varphi}\|^2 + 4)\varepsilon \end{align*} $$
whenever
![]() $n> N$
.
$n> N$
.
In this example,
![]() $\varphi $
has an angular derivative at
$\varphi $
has an angular derivative at
![]() $z = 1$
because
$z = 1$
because
![]() $(1 - \varphi (z)) / (1 - z) = 1 / 2$
. Then it follows from [Reference Cowen and MacCluer3, Corollary 3.14] that
$(1 - \varphi (z)) / (1 - z) = 1 / 2$
. Then it follows from [Reference Cowen and MacCluer3, Corollary 3.14] that
![]() $C_{\varphi }$
is not compact on
$C_{\varphi }$
is not compact on
![]() $A^2_{\alpha }$
. However,
$A^2_{\alpha }$
. However,
![]() $uC_{\varphi }$
is compact.
$uC_{\varphi }$
is compact.
There is another question of interest: does the compactness of
![]() $C_{\varphi }$
guarantee that of
$C_{\varphi }$
guarantee that of
![]() $uC_{\varphi }$
? The answer to this question is generally no, at least when u is unbounded on D. To see this, we first state a necessary condition for
$uC_{\varphi }$
? The answer to this question is generally no, at least when u is unbounded on D. To see this, we first state a necessary condition for
![]() $uC_{\varphi }$
to be compact.
$uC_{\varphi }$
to be compact.
Theorem 2.4. If
![]() $uC_{\varphi }$
is a compact weighted composition operator on
$uC_{\varphi }$
is a compact weighted composition operator on
![]() $A^2_{\alpha }$
, then
$A^2_{\alpha }$
, then
 $$ \begin{align} \lim_{|z| \to 1^-} |u(z)|\bigg(\frac{1 - |z|^2}{1 - |\varphi(z)|^2}\bigg)^{{\alpha}/{2} + 1} = 0. \end{align} $$
$$ \begin{align} \lim_{|z| \to 1^-} |u(z)|\bigg(\frac{1 - |z|^2}{1 - |\varphi(z)|^2}\bigg)^{{\alpha}/{2} + 1} = 0. \end{align} $$
This theorem is a simple generalization of [Reference Čučković and Zhao4, Proposition 1]: since
 $$ \begin{align*}\|(uC_{\varphi})^*K_z\| = (1 - |z|^2)^{{\alpha}/{2} + 1}|u(z)|\|k_{\varphi(z)}\| = |u(z)|\bigg(\frac{1 - |z|^2}{1 - |\varphi(z)|^2}\bigg)^{{\alpha}/{2} + 1}, \end{align*} $$
$$ \begin{align*}\|(uC_{\varphi})^*K_z\| = (1 - |z|^2)^{{\alpha}/{2} + 1}|u(z)|\|k_{\varphi(z)}\| = |u(z)|\bigg(\frac{1 - |z|^2}{1 - |\varphi(z)|^2}\bigg)^{{\alpha}/{2} + 1}, \end{align*} $$
where
![]() $K_z$
is the normalized reproducing kernel corresponding to the point evaluation functional on
$K_z$
is the normalized reproducing kernel corresponding to the point evaluation functional on
![]() $A^2_{\alpha }$
at z, the condition in Equation (2-1) follows from the compactness of
$A^2_{\alpha }$
at z, the condition in Equation (2-1) follows from the compactness of
![]() $(uC_{\varphi })^*$
and the result that
$(uC_{\varphi })^*$
and the result that
![]() $K_z \to 0$
weakly in
$K_z \to 0$
weakly in
![]() $A^2_{\alpha }$
as
$A^2_{\alpha }$
as
![]() $|z| \to 1^-$
.
$|z| \to 1^-$
.
While the validity of the converse of Theorem 2.4 awaits further investigation, the condition in Equation (2-1) actually is equivalent to the compactness of composition operators on
![]() $A^2_{\alpha }$
[Reference Zhu17, Theorem 11.8]. Under additional assumptions on u and
$A^2_{\alpha }$
[Reference Zhu17, Theorem 11.8]. Under additional assumptions on u and
![]() $\varphi $
, however, the condition in Equation (2-1) does characterize the compactness of
$\varphi $
, however, the condition in Equation (2-1) does characterize the compactness of
![]() $uC_{\varphi }$
. This will be shown in Theorem 2.8.
$uC_{\varphi }$
. This will be shown in Theorem 2.8.
Example 2.5. Let
![]() $u(z) = 1 / (1 - z)^{1/2 + {\alpha }/{4}}$
and
$u(z) = 1 / (1 - z)^{1/2 + {\alpha }/{4}}$
and
![]() $\varphi (z) = 1 - (1 - z)^{1/2}$
. From [Reference Lo and Loh10, Example 3.4],
$\varphi (z) = 1 - (1 - z)^{1/2}$
. From [Reference Lo and Loh10, Example 3.4],
![]() $\varphi $
has no finite angular derivative at any point of T. Thus,
$\varphi $
has no finite angular derivative at any point of T. Thus,
![]() $C_{\varphi }$
is compact by [Reference Cowen and MacCluer3, Theorem 3.22]. However,
$C_{\varphi }$
is compact by [Reference Cowen and MacCluer3, Theorem 3.22]. However,
 $$ \begin{align*}\lim_{r \to 1^-} u(r)\bigg[\frac{1 - r^2}{1 - (\varphi(r))^2}\bigg]^{{\alpha}/{2} + 1} = \lim_{r \to 1^-} \bigg[\frac{1 + r}{2- (1 - r)^{{1}/{2}}}\bigg]^{{\alpha}/{2} + 1} = 1 \ (\ne 0). \end{align*} $$
$$ \begin{align*}\lim_{r \to 1^-} u(r)\bigg[\frac{1 - r^2}{1 - (\varphi(r))^2}\bigg]^{{\alpha}/{2} + 1} = \lim_{r \to 1^-} \bigg[\frac{1 + r}{2- (1 - r)^{{1}/{2}}}\bigg]^{{\alpha}/{2} + 1} = 1 \ (\ne 0). \end{align*} $$
According to Theorem 2.4,
![]() $uC_{\varphi }$
is not compact on
$uC_{\varphi }$
is not compact on
![]() $A^2_{\alpha }$
.
$A^2_{\alpha }$
.
When
![]() $C_{\varphi }$
is compact, how can we choose u such that
$C_{\varphi }$
is compact, how can we choose u such that
![]() $uC_{\varphi }$
is compact? The next result provides one criterion. Its statement and proof are similar to those of [Reference Lo and Loh10, Theorem 4.1].
$uC_{\varphi }$
is compact? The next result provides one criterion. Its statement and proof are similar to those of [Reference Lo and Loh10, Theorem 4.1].
Theorem 2.6. Suppose
![]() $u \in A^2_{\alpha }$
and
$u \in A^2_{\alpha }$
and
![]() $C_{\varphi }$
is compact on
$C_{\varphi }$
is compact on
![]() $A^2_{\alpha }$
. If there is a constant c with
$A^2_{\alpha }$
. If there is a constant c with
![]() $0 < c < 1$
such that u is bounded on the set
$0 < c < 1$
such that u is bounded on the set
![]() $\{z \in D : |\varphi (z)|> c\}$
, then
$\{z \in D : |\varphi (z)|> c\}$
, then
![]() $uC_{\varphi }$
is compact on
$uC_{\varphi }$
is compact on
![]() $A^2_{\alpha }$
.
$A^2_{\alpha }$
.
We prove a ‘converse’ of Theorem 2.4 with extra assumptions on u and
![]() $\varphi $
. While Moorhouse showed that the condition in Equation (2-1) characterizes the compactness of
$\varphi $
. While Moorhouse showed that the condition in Equation (2-1) characterizes the compactness of
![]() $uC_{\varphi }$
when u is bounded on D [Reference Moorhouse14, Corollary 1], the validity of our result does not require the boundedness of u. The following lemma is needed.
$uC_{\varphi }$
when u is bounded on D [Reference Moorhouse14, Corollary 1], the validity of our result does not require the boundedness of u. The following lemma is needed.
Lemma 2.7. If
![]() $f \in A^2_{\alpha }$
, then
$f \in A^2_{\alpha }$
, then
where
![]() $c := \min \{1, [(\alpha + 1)(\alpha + 2)] / (\alpha + 3)\}$
and
$c := \min \{1, [(\alpha + 1)(\alpha + 2)] / (\alpha + 3)\}$
and
![]() $d := \max \{1, (\alpha + 1)(\alpha + 2)\}$
.
$d := \max \{1, (\alpha + 1)(\alpha + 2)\}$
.
The proof of this lemma is direct and follows from a straightforward computation of the integral
![]() $\int _D |f'(z)|^2 (1 - |z|^2)^2 \,dA_{\alpha }(z)$
in terms of the Taylor coefficients of f. An immediate consequence of Lemma 2.7 is that
$\int _D |f'(z)|^2 (1 - |z|^2)^2 \,dA_{\alpha }(z)$
in terms of the Taylor coefficients of f. An immediate consequence of Lemma 2.7 is that
![]() $f \in A^2_{\alpha }$
if and only if
$f \in A^2_{\alpha }$
if and only if
![]() $f' \in L^2(D, dA_{\alpha + 2})$
. Indeed, this is a particular case of a more general result in [Reference Hedenmalm, Korenblum and Zhu8, Proposition 1.11]. Moreover, the lemma implies that
$f' \in L^2(D, dA_{\alpha + 2})$
. Indeed, this is a particular case of a more general result in [Reference Hedenmalm, Korenblum and Zhu8, Proposition 1.11]. Moreover, the lemma implies that
![]() $\|f\|$
is equivalent to
$\|f\|$
is equivalent to
![]() $\|f'\|_{A_{\alpha + 2}^2}$
if
$\|f'\|_{A_{\alpha + 2}^2}$
if
![]() $f \in A^2_{\alpha }$
and
$f \in A^2_{\alpha }$
and
![]() $f(0)=0$
.
$f(0)=0$
.
Theorem 2.8. Let
![]() $uC_{\varphi }$
be a weighted composition operator on
$uC_{\varphi }$
be a weighted composition operator on
![]() $A^2_{\alpha }$
. If
$A^2_{\alpha }$
. If
-
(i)
 $\varphi $
is univalent on D;
$\varphi $
is univalent on D; -
(ii)
 $ \lim _{|z| \to 1^-} |u'(z)|(1 - |z|^2) = 0$
; and
$ \lim _{|z| \to 1^-} |u'(z)|(1 - |z|^2) = 0$
; and -
(iii)
 $ \lim _{|z| \to 1^-} |u(z)|(({1 - |z|^2})/({1 - |\varphi (z)|^2}))^{{\alpha }/{2} + 1} = 0$
;
$ \lim _{|z| \to 1^-} |u(z)|(({1 - |z|^2})/({1 - |\varphi (z)|^2}))^{{\alpha }/{2} + 1} = 0$
;
then
![]() $uC_{\varphi }$
is compact on
$uC_{\varphi }$
is compact on
![]() $A^2_{\alpha }$
.
$A^2_{\alpha }$
.
Proof. Fix any
![]() $\varepsilon> 0$
. By conditions (ii) and (iii), there is a constant r with
$\varepsilon> 0$
. By conditions (ii) and (iii), there is a constant r with
![]() ${1 / 2 < r < 1}$
such that
${1 / 2 < r < 1}$
such that
whenever
![]() $r < |z| < 1$
. Let
$r < |z| < 1$
. Let
![]() $\{f_n\}_{n = 1}^{\infty }$
be a sequence in
$\{f_n\}_{n = 1}^{\infty }$
be a sequence in
![]() $A^2_{\alpha }$
with
$A^2_{\alpha }$
with
![]() $\|f_n\| \leq 1$
for all
$\|f_n\| \leq 1$
for all
![]() $n \in {\mathbb N}$
and
$n \in {\mathbb N}$
and
![]() $f_n \to 0$
uniformly on compact subsets of D. By Lemma 2.7,
$f_n \to 0$
uniformly on compact subsets of D. By Lemma 2.7,
where c is the constant defined in Lemma 2.7. Then
so that
where
 $$ \begin{align*}A_n := \int_{\overline{S(0, r)}} |u(z)|^2 |f_n'(\varphi(z))|^2 |\varphi'(z)|^2 (1 - |z|^2)^2\, dA_{\alpha}(z), \end{align*} $$
$$ \begin{align*}A_n := \int_{\overline{S(0, r)}} |u(z)|^2 |f_n'(\varphi(z))|^2 |\varphi'(z)|^2 (1 - |z|^2)^2\, dA_{\alpha}(z), \end{align*} $$
 $$ \begin{align*}B_n := \int_{D \setminus \overline{S(0, r)}} |u(z)|^2 |f_n'(\varphi(z))|^2 |\varphi'(z)|^2 (1 - |z|^2)^2\, dA_{\alpha}(z), \end{align*} $$
$$ \begin{align*}B_n := \int_{D \setminus \overline{S(0, r)}} |u(z)|^2 |f_n'(\varphi(z))|^2 |\varphi'(z)|^2 (1 - |z|^2)^2\, dA_{\alpha}(z), \end{align*} $$
 $$ \begin{align*}C_n := \int_{\overline{S(0, r)}} |u'(z)|^2 |f_n(\varphi(z))|^2 (1 - |z|^2)^2\, dA_{\alpha}(z), \end{align*} $$
$$ \begin{align*}C_n := \int_{\overline{S(0, r)}} |u'(z)|^2 |f_n(\varphi(z))|^2 (1 - |z|^2)^2\, dA_{\alpha}(z), \end{align*} $$
and
 $$ \begin{align*}D_n := \int_{D \setminus \overline{S(0, r)}} |u'(z)|^2 |f_n(\varphi(z))|^2 (1 - |z|^2)^2\, dA_{\alpha}(z). \end{align*} $$
$$ \begin{align*}D_n := \int_{D \setminus \overline{S(0, r)}} |u'(z)|^2 |f_n(\varphi(z))|^2 (1 - |z|^2)^2\, dA_{\alpha}(z). \end{align*} $$
Both sets
![]() $\{\varphi (0)\}$
and
$\{\varphi (0)\}$
and
![]() $\varphi (\overline {S(0, r)})$
are compact in D. Thus, there exists some
$\varphi (\overline {S(0, r)})$
are compact in D. Thus, there exists some
![]() $N \in {\mathbb N}$
for which if
$N \in {\mathbb N}$
for which if
![]() $n> N$
and
$n> N$
and
![]() $z \in \overline {S(0, r)}$
, then
$z \in \overline {S(0, r)}$
, then
From the continuity of
![]() $u\varphi '$
and
$u\varphi '$
and
![]() $u'$
on the compact set
$u'$
on the compact set
![]() $\overline {S(0, r)}$
, there is a positive constant M such that
$\overline {S(0, r)}$
, there is a positive constant M such that
for all
![]() $z \in \overline {S(0, r)}$
. Therefore, if
$z \in \overline {S(0, r)}$
. Therefore, if
![]() $n> N$
, we have
$n> N$
, we have
 $$\begin{align} A_n + C_n \leq 2M\varepsilon \int_{\overline{S(0, r)}}\, dA_{\alpha}(z) \leq 2M\varepsilon \int_D\, dA_{\alpha}(z) = 2M\varepsilon. \end{align} $$
$$\begin{align} A_n + C_n \leq 2M\varepsilon \int_{\overline{S(0, r)}}\, dA_{\alpha}(z) \leq 2M\varepsilon \int_D\, dA_{\alpha}(z) = 2M\varepsilon. \end{align} $$
The boundedness of
![]() $C_{\varphi }$
on
$C_{\varphi }$
on
![]() $A^2_{\alpha }$
implies that
$A^2_{\alpha }$
implies that
 $$\begin{align} D_n \leq \varepsilon\int_{D \setminus \overline{S(0, r)}} |f_n(\varphi(z))|^2\, dA_{\alpha}(z) \leq \varepsilon\|C_{\varphi}f_n\|^2 \leq \|C_{\varphi}\|^2 \varepsilon. \end{align} $$
$$\begin{align} D_n \leq \varepsilon\int_{D \setminus \overline{S(0, r)}} |f_n(\varphi(z))|^2\, dA_{\alpha}(z) \leq \varepsilon\|C_{\varphi}f_n\|^2 \leq \|C_{\varphi}\|^2 \varepsilon. \end{align} $$
It remains to estimate
![]() $B_n$
. Note that
$B_n$
. Note that
 $$ \begin{align*} B_n & = (\alpha + 1)\int_{D \setminus \overline{S(0, r)}} |u(z)|^2 |f_n'(\varphi(z))|^2 |\varphi'(z)|^2 (1 - |z|^2)^{\alpha + 2}\, dA(z) \\[3pt] & \leq (\alpha + 1)\varepsilon\int_{D \setminus \overline{S(0, r)}} |f_n'(\varphi(z))|^2 |\varphi'(z)|^2 (1 - |\varphi(z)|^2)^{\alpha + 2}\, dA(z). \end{align*} $$
$$ \begin{align*} B_n & = (\alpha + 1)\int_{D \setminus \overline{S(0, r)}} |u(z)|^2 |f_n'(\varphi(z))|^2 |\varphi'(z)|^2 (1 - |z|^2)^{\alpha + 2}\, dA(z) \\[3pt] & \leq (\alpha + 1)\varepsilon\int_{D \setminus \overline{S(0, r)}} |f_n'(\varphi(z))|^2 |\varphi'(z)|^2 (1 - |\varphi(z)|^2)^{\alpha + 2}\, dA(z). \end{align*} $$
Put
![]() $w = \varphi (z)$
. By the change-of-variable formula in [Reference MacCluer and Shapiro11, page 891] and the univalence of
$w = \varphi (z)$
. By the change-of-variable formula in [Reference MacCluer and Shapiro11, page 891] and the univalence of
![]() $\varphi $
,
$\varphi $
,
 $$ \begin{align} B_n & \leq (\alpha + 1)\varepsilon\int_D |f_n'(w)|^2 (1 - |w|^2)^{\alpha + 2}\, dA(w) \nonumber \\[3pt] & \leq \varepsilon\int_D |f_n'(w)|^2 (1 - |w|^2)^2\, dA_{\alpha}(w) \nonumber \\[3pt] & \leq \varepsilon d\|f_n\|^2 \nonumber \\[3pt] & \leq \varepsilon d , \end{align} $$
$$ \begin{align} B_n & \leq (\alpha + 1)\varepsilon\int_D |f_n'(w)|^2 (1 - |w|^2)^{\alpha + 2}\, dA(w) \nonumber \\[3pt] & \leq \varepsilon\int_D |f_n'(w)|^2 (1 - |w|^2)^2\, dA_{\alpha}(w) \nonumber \\[3pt] & \leq \varepsilon d\|f_n\|^2 \nonumber \\[3pt] & \leq \varepsilon d , \end{align} $$
where d is the constant defined in Lemma 2.7. From Equations (2-2)–(2-6), it now follows that
for all
![]() $n> N$
. Hence,
$n> N$
. Hence,
![]() $\|uC_{\varphi }f_n\| \to 0$
as
$\|uC_{\varphi }f_n\| \to 0$
as
![]() $n \to \infty $
.
$n \to \infty $
.
3 Hilbert–Schmidt weighted composition operators
An important class of compact operators is the Hilbert–Schmidt operators. Let
![]() $H_1$
and
$H_1$
and
![]() $H_2$
be separable Hilbert spaces and
$H_2$
be separable Hilbert spaces and
![]() $T : H_1 \to H_2$
be a bounded linear operator. Then T is said to be Hilbert–Schmidt if
$T : H_1 \to H_2$
be a bounded linear operator. Then T is said to be Hilbert–Schmidt if
![]() $\sum _{k=0}^{\infty } \|T e_k\|_{H_2}^2 < \infty $
for some orthonormal basis
$\sum _{k=0}^{\infty } \|T e_k\|_{H_2}^2 < \infty $
for some orthonormal basis
![]() $\{e_k\}_{k=0}^{\infty }$
of
$\{e_k\}_{k=0}^{\infty }$
of
![]() $H_1$
. The value of this sum is independent of the choice of an orthonormal basis. It is well known that every Hilbert–Schmidt operator is compact, but the converse is not necessarily true. In what follows, we take
$H_1$
. The value of this sum is independent of the choice of an orthonormal basis. It is well known that every Hilbert–Schmidt operator is compact, but the converse is not necessarily true. In what follows, we take
![]() $\{e_k\}_{k=0}^{\infty }$
to be the standard orthonormal basis for
$\{e_k\}_{k=0}^{\infty }$
to be the standard orthonormal basis for
![]() $A^2_{\alpha }$
, as given by Equation (1-1) in Section 1. We also recall a few identities for useful reference:
$A^2_{\alpha }$
, as given by Equation (1-1) in Section 1. We also recall a few identities for useful reference:
-
(a)
 $ {1}/{(1 - x)^{\alpha + 2}} = \sum _{k=0}^{\infty } ({\Gamma (\alpha + 2 + k)}/{k! \,\Gamma (\alpha + 2)}) x^k$
for
$ {1}/{(1 - x)^{\alpha + 2}} = \sum _{k=0}^{\infty } ({\Gamma (\alpha + 2 + k)}/{k! \,\Gamma (\alpha + 2)}) x^k$
for
 $|x| < 1$
;
$|x| < 1$
; -
(b)
 $ 1 - |({w - z})/({1 - \overline {w}z})|^2 = {(1 - |w|^2)(1 - |z|^2)}/{|1 - \overline {w}z|^2}$
and
$ 1 - |({w - z})/({1 - \overline {w}z})|^2 = {(1 - |w|^2)(1 - |z|^2)}/{|1 - \overline {w}z|^2}$
and
 $ 1 - \overline {w}(({w - z})/ ({1 - \overline {w}z})) = ({1 - |w|^2})/({1 - \overline {w}z})$
for every
$ 1 - \overline {w}(({w - z})/ ({1 - \overline {w}z})) = ({1 - |w|^2})/({1 - \overline {w}z})$
for every
 $w, z \in D$
.
$w, z \in D$
.
Using the criterion for
![]() $uC_{\varphi }$
to belong to the Schatten class, Čučković and Zhao obtained a characterization for Hilbert–Schmidt weighted composition maps on
$uC_{\varphi }$
to belong to the Schatten class, Čučković and Zhao obtained a characterization for Hilbert–Schmidt weighted composition maps on
![]() $A^2_0$
[Reference Čučković and Zhao4, Corollary 3]. We first generalize this result to the weighted Bergman space and provide a direct proof.
$A^2_0$
[Reference Čučković and Zhao4, Corollary 3]. We first generalize this result to the weighted Bergman space and provide a direct proof.
Theorem 3.1. Let
![]() $uC_{\varphi }$
be a weighted composition operator on
$uC_{\varphi }$
be a weighted composition operator on
![]() $A^2_{\alpha }$
. Then
$A^2_{\alpha }$
. Then
![]() $uC_{\varphi }$
is Hilbert–Schmidt if and only if
$uC_{\varphi }$
is Hilbert–Schmidt if and only if
 $$ \begin{align} \int_D \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) < \infty. \end{align} $$
$$ \begin{align} \int_D \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) < \infty. \end{align} $$
Proof. Direct computation gives
 $$ \begin{align*} \sum_{k=0}^{\infty} \|uC_{\varphi} e_k\|^2 & = \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} \int_D |u(z)|^2 |\varphi(z)|^{2k}\, dA_{\alpha}(z) \\[3pt] & = \int_D |u(z)|^2 \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} |\varphi(z)|^{2k}\, dA_{\alpha}(z) \\[3pt] & = \int_D \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z). \end{align*} $$
$$ \begin{align*} \sum_{k=0}^{\infty} \|uC_{\varphi} e_k\|^2 & = \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} \int_D |u(z)|^2 |\varphi(z)|^{2k}\, dA_{\alpha}(z) \\[3pt] & = \int_D |u(z)|^2 \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} |\varphi(z)|^{2k}\, dA_{\alpha}(z) \\[3pt] & = \int_D \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z). \end{align*} $$
Interchanging the summation and integral sums in the second equality is legitimate because the terms are all non-negative. The assertion now follows.
It is shown in Theorem 2.2 that if
![]() $\overline {\varphi (D)} \subset D$
, then
$\overline {\varphi (D)} \subset D$
, then
![]() $uC_{\varphi }$
is compact. By Theorem 3.1,
$uC_{\varphi }$
is compact. By Theorem 3.1,
![]() $uC_{\varphi }$
is also Hilbert–Schmidt. The next result shows that when
$uC_{\varphi }$
is also Hilbert–Schmidt. The next result shows that when
![]() $\varphi $
is an automorphism of D, the characterization of when a weighted composition operator is Hilbert–Schmidt becomes simpler.
$\varphi $
is an automorphism of D, the characterization of when a weighted composition operator is Hilbert–Schmidt becomes simpler.
Corollary 3.2. Let
![]() $\varphi $
be an automorphism of D. Then the weighted composition operator
$\varphi $
be an automorphism of D. Then the weighted composition operator
![]() $uC_{\varphi }$
is Hilbert–Schmidt on
$uC_{\varphi }$
is Hilbert–Schmidt on
![]() $A^2_{\alpha }$
if and only if
$A^2_{\alpha }$
if and only if
 $$ \begin{align} \int_D \frac{|u(z)|^2}{(1 - |z|^2)^2} \, dA(z) < \infty. \end{align} $$
$$ \begin{align} \int_D \frac{|u(z)|^2}{(1 - |z|^2)^2} \, dA(z) < \infty. \end{align} $$
Proof. By the Schwarz–Pick theorem [Reference Cowen and MacCluer3, page 48], we have
 $$ \begin{align*}\frac{1 - |\varphi(z)|}{1 - |z|} \geq \frac{1 - |\varphi(0)|}{1 + |\varphi(0)|}. \end{align*} $$
$$ \begin{align*}\frac{1 - |\varphi(z)|}{1 - |z|} \geq \frac{1 - |\varphi(0)|}{1 + |\varphi(0)|}. \end{align*} $$
Thus,
 $$ \begin{align} \frac{|u(z)|^2}{(1 - |z|^2)^{\alpha + 2}} \geq \bigg(\frac{1}{2} \cdot \frac{1 - |\varphi(0)|}{1 + |\varphi(0)|}\bigg)^{\alpha + 2}\frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}}. \end{align} $$
$$ \begin{align} \frac{|u(z)|^2}{(1 - |z|^2)^{\alpha + 2}} \geq \bigg(\frac{1}{2} \cdot \frac{1 - |\varphi(0)|}{1 + |\varphi(0)|}\bigg)^{\alpha + 2}\frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}}. \end{align} $$
Write
![]() $\varphi (z) = c(a - z) / (1 - \overline {a}z)$
, where
$\varphi (z) = c(a - z) / (1 - \overline {a}z)$
, where
![]() $a \in D$
and
$a \in D$
and
![]() $|c| = 1$
. Since
$|c| = 1$
. Since
 $$ \begin{align*}1 - |\varphi(z)|^2 = \frac{(1 - |a|^2)(1 - |z|^2)}{|1 - \overline{a}z|^2} \quad\mathrm{and}\quad |1 -\overline{a}z| \geq 1 - |a| \end{align*} $$
$$ \begin{align*}1 - |\varphi(z)|^2 = \frac{(1 - |a|^2)(1 - |z|^2)}{|1 - \overline{a}z|^2} \quad\mathrm{and}\quad |1 -\overline{a}z| \geq 1 - |a| \end{align*} $$
for every
![]() $z \in D$
, it follows that
$z \in D$
, it follows that
 $$ \begin{align} \frac{|u(z)|^2}{(1 - |z|^2)^{\alpha + 2}} \leq \bigg(\frac{1 + |a|}{1 - |a|}\bigg)^{\alpha + 2}\frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}}. \end{align} $$
$$ \begin{align} \frac{|u(z)|^2}{(1 - |z|^2)^{\alpha + 2}} \leq \bigg(\frac{1 + |a|}{1 - |a|}\bigg)^{\alpha + 2}\frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}}. \end{align} $$
We obtain the desired result by combining Equations (3-3) and (3-4), Theorem 3.1, and the fact that
![]() ${dA_{\alpha }(z) \kern1.2pt{=}\kern1.2pt (\alpha + 1) (1 - |z|^2)^{\alpha } dA(z)}$
.
${dA_{\alpha }(z) \kern1.2pt{=}\kern1.2pt (\alpha + 1) (1 - |z|^2)^{\alpha } dA(z)}$
.
The condition in Equation (3-2) is independent of the parameter
![]() $\alpha $
and can be expressed as ‘
$\alpha $
and can be expressed as ‘
![]() $u \in L^2(D, d\tau )$
’, where
$u \in L^2(D, d\tau )$
’, where
![]() $\tau $
is the Möbius invariant measure on D defined by
$\tau $
is the Möbius invariant measure on D defined by
Here the term ‘invariant measure’ is justified by the fact that if
![]() $\varphi $
is an automorphism of D, then
$\varphi $
is an automorphism of D, then
for all analytic functions f on D [Reference Zhu17, Section 5.3.1].
Corollary 3.2 is also in contrast to the corresponding result for the Hardy space
![]() $H^2$
of D: if
$H^2$
of D: if
![]() $\varphi $
is an automorphism, then it follows from [Reference Matache12, Theorem 9] that the only Hilbert–Schmidt weighted composition operator on
$\varphi $
is an automorphism, then it follows from [Reference Matache12, Theorem 9] that the only Hilbert–Schmidt weighted composition operator on
![]() $H^2$
is the zero operator.
$H^2$
is the zero operator.
Example 3.3. Let
![]() $u(z) = 1 / (1 - z)^{1/4}$
and
$u(z) = 1 / (1 - z)^{1/4}$
and
![]() $\varphi $
be any automorphism of D. Since, for all
$\varphi $
be any automorphism of D. Since, for all
![]() $z \in D$
we have
$z \in D$
we have
![]() $1 - |z|^2 \leq 2|1-z|$
, it follows that
$1 - |z|^2 \leq 2|1-z|$
, it follows that
 $$ \begin{align*} \int_D \frac{|u(z)|^2}{(1 - |z|^2)^2} \, dA(z) & = \int_D \frac{1}{|1-z|^{{1}/{2}}(1 - |z|^2)^2} \, dA(z) \\[3pt] & \geq \frac{1}{4}\int_D \frac{1}{|1-z|^{{5}/{2}}} \, dA(z). \end{align*} $$
$$ \begin{align*} \int_D \frac{|u(z)|^2}{(1 - |z|^2)^2} \, dA(z) & = \int_D \frac{1}{|1-z|^{{1}/{2}}(1 - |z|^2)^2} \, dA(z) \\[3pt] & \geq \frac{1}{4}\int_D \frac{1}{|1-z|^{{5}/{2}}} \, dA(z). \end{align*} $$
By [Reference Cowen and MacCluer3, Lemma 7.3],
![]() $\int _D ({1}/{|1-z|^{5 / 2}}) \, dA(z) = \infty $
. According to Corollary 3.2,
$\int _D ({1}/{|1-z|^{5 / 2}}) \, dA(z) = \infty $
. According to Corollary 3.2,
![]() $uC_{\varphi }$
is not Hilbert–Schmidt on
$uC_{\varphi }$
is not Hilbert–Schmidt on
![]() $A^2_{\alpha }$
.
$A^2_{\alpha }$
.
The inequality in Equation (3-3) in fact holds for all analytic self-maps
![]() $\varphi $
of D. Thus, Equation (3-2) provides a sufficient condition for
$\varphi $
of D. Thus, Equation (3-2) provides a sufficient condition for
![]() $uC_{\varphi }$
to be Hilbert–Schmidt on
$uC_{\varphi }$
to be Hilbert–Schmidt on
![]() $A^2_{\alpha }$
. However, this condition is not necessary, as shown by the following example.
$A^2_{\alpha }$
. However, this condition is not necessary, as shown by the following example.
Example 3.4. Let
![]() $u(z) = (1 - z)^{(\alpha + 1) / 4}$
and
$u(z) = (1 - z)^{(\alpha + 1) / 4}$
and
![]() $\varphi (z) = 1 - (1 - z)^{1/2}$
. Then
$\varphi (z) = 1 - (1 - z)^{1/2}$
. Then
![]() $u \in A^2_{\alpha }$
. We claim that
$u \in A^2_{\alpha }$
. We claim that
![]() $uC_{\varphi }$
is Hilbert–Schmidt on
$uC_{\varphi }$
is Hilbert–Schmidt on
![]() $A^2_{\alpha }$
. Since
$A^2_{\alpha }$
. Since
![]() $\varphi $
takes D into a polygonal region inscribed in T, there exist positive constants
$\varphi $
takes D into a polygonal region inscribed in T, there exist positive constants
![]() $c, \delta $
such that
$c, \delta $
such that
![]() $\delta < 1/2$
, and
$\delta < 1/2$
, and
![]() $1 - |\varphi (z)| \geq c|1 - z|^{1/2}$
on
$1 - |\varphi (z)| \geq c|1 - z|^{1/2}$
on
![]() $S(1, \delta )$
. Write
$S(1, \delta )$
. Write
 $$ \begin{align*} & \int_D \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) \\[3pt] &\quad = \int_{S(1, \delta)} \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) + \int_{D \setminus S(1, \delta)} \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z). \end{align*} $$
$$ \begin{align*} & \int_D \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) \\[3pt] &\quad = \int_{S(1, \delta)} \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) + \int_{D \setminus S(1, \delta)} \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z). \end{align*} $$
By choosing
![]() $1 + {\alpha }/{2} < \beta < \tfrac 32 + \alpha $
, we have
$1 + {\alpha }/{2} < \beta < \tfrac 32 + \alpha $
, we have
for
![]() $z \in S(1, \delta )$
. Thus,
$z \in S(1, \delta )$
. Thus,
 $$ \begin{align*} \int_{S(1, \delta)} \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) & \leq \frac{1}{c^{\alpha + 2}}\int_{S(1, \delta)} \frac{1}{|1 - z|^{\beta - ({\alpha + 1})/{2}}} \, dA_{\alpha}(z) \\[3pt] & \leq \frac{1}{c^{\alpha + 2}}\int_D \frac{1}{|1 - z|^{\beta - ({\alpha + 1})/{2}}} \, dA_{\alpha}(z) \\[3pt] & < \infty, \end{align*} $$
$$ \begin{align*} \int_{S(1, \delta)} \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) & \leq \frac{1}{c^{\alpha + 2}}\int_{S(1, \delta)} \frac{1}{|1 - z|^{\beta - ({\alpha + 1})/{2}}} \, dA_{\alpha}(z) \\[3pt] & \leq \frac{1}{c^{\alpha + 2}}\int_D \frac{1}{|1 - z|^{\beta - ({\alpha + 1})/{2}}} \, dA_{\alpha}(z) \\[3pt] & < \infty, \end{align*} $$
since
![]() $|\,\beta - ({\alpha + 1})/{2}| < 1 + {\alpha }/{2}$
. On
$|\,\beta - ({\alpha + 1})/{2}| < 1 + {\alpha }/{2}$
. On
![]() $D \setminus S(1, \delta )$
, the continuity of
$D \setminus S(1, \delta )$
, the continuity of
![]() $\varphi $
ensures that
$\varphi $
ensures that
![]() $|\varphi (z)| \leq d$
for a constant d with
$|\varphi (z)| \leq d$
for a constant d with
![]() $0 < d < 1$
. Then
$0 < d < 1$
. Then
 $$ \begin{align*} \int_{D \setminus S(1, \delta)} \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) & \leq \frac{1}{(1 - d^2)^{\alpha + 2}}\int_{D \setminus S(1, \delta)} |u(z)|^2\, dA_{\alpha}(z) \\[3pt] & \leq \frac{1}{(1 - d^2)^{\alpha + 2}}\|u\|^2 \\[3pt] & < \infty. \end{align*} $$
$$ \begin{align*} \int_{D \setminus S(1, \delta)} \frac{|u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) & \leq \frac{1}{(1 - d^2)^{\alpha + 2}}\int_{D \setminus S(1, \delta)} |u(z)|^2\, dA_{\alpha}(z) \\[3pt] & \leq \frac{1}{(1 - d^2)^{\alpha + 2}}\|u\|^2 \\[3pt] & < \infty. \end{align*} $$
From Theorem 3.1,
![]() $uC_{\varphi }$
is Hilbert–Schmidt. However, since
$uC_{\varphi }$
is Hilbert–Schmidt. However, since
![]() $1 - |z|^2 \leq 2|1 - z|$
on D, we have
$1 - |z|^2 \leq 2|1 - z|$
on D, we have
 $$ \begin{align*}\int_D \frac{|u(z)|^2}{(1 - |z|^2)^2} \, dA(z) \geq \frac{1}{4}\int_D \frac{1}{|1 - z|^{({3 - \alpha})/{2}}} \, dA(z) = \infty, \end{align*} $$
$$ \begin{align*}\int_D \frac{|u(z)|^2}{(1 - |z|^2)^2} \, dA(z) \geq \frac{1}{4}\int_D \frac{1}{|1 - z|^{({3 - \alpha})/{2}}} \, dA(z) = \infty, \end{align*} $$
provided that
![]() $|(3 - \alpha ) / 2| \geq 1$
, that is,
$|(3 - \alpha ) / 2| \geq 1$
, that is,
![]() $-1 < \alpha \leq 1$
or
$-1 < \alpha \leq 1$
or
![]() $\alpha \geq 5$
.
$\alpha \geq 5$
.
The rest of this section is devoted to characterizing when
![]() $uC_{\varphi } - vC_{\psi }$
on
$uC_{\varphi } - vC_{\psi }$
on
![]() $A^2_{\alpha }$
is Hilbert–Schmidt, where v and
$A^2_{\alpha }$
is Hilbert–Schmidt, where v and
![]() $\psi $
are two analytic functions on D such that
$\psi $
are two analytic functions on D such that
![]() $\psi (D) \subset D$
. This problem originates from the study of the topological structure of the space of (weighted) composition operators on
$\psi (D) \subset D$
. This problem originates from the study of the topological structure of the space of (weighted) composition operators on
![]() $A^2_{\alpha }$
. There has been extensive investigation about differences of composition operators on the Hardy space
$A^2_{\alpha }$
. There has been extensive investigation about differences of composition operators on the Hardy space
![]() $H^2$
of D (see for example [Reference Bourdon1, Reference Gallardo-Gutiérrez, González, Nieminen and Saksman6, Reference Shapiro and Sundberg16]). The compact difference of two composition operators between weighted Bergman spaces was completely characterized in [Reference Lindstrom and Saukko9, Reference Moorhouse14, Reference Saukko15].
$H^2$
of D (see for example [Reference Bourdon1, Reference Gallardo-Gutiérrez, González, Nieminen and Saksman6, Reference Shapiro and Sundberg16]). The compact difference of two composition operators between weighted Bergman spaces was completely characterized in [Reference Lindstrom and Saukko9, Reference Moorhouse14, Reference Saukko15].
In [Reference Choe, Hosokawa and Koo2], Choe et al. topologized the space of composition operators on
![]() $A^2_{\alpha }$
and described its components. By putting
$A^2_{\alpha }$
and described its components. By putting
 $$ \begin{align*}\phi(z) = \frac{\psi(z) - \varphi(z)}{1 - \overline{\psi(z)}\varphi(z)} \end{align*} $$
$$ \begin{align*}\phi(z) = \frac{\psi(z) - \varphi(z)}{1 - \overline{\psi(z)}\varphi(z)} \end{align*} $$
for
![]() $z \in D$
, they also characterized the Hilbert–Schmidt difference of two composition operators
$z \in D$
, they also characterized the Hilbert–Schmidt difference of two composition operators
![]() $C_{\varphi }$
and
$C_{\varphi }$
and
![]() $C_{\psi }$
in terms of
$C_{\psi }$
in terms of
![]() $|\phi |$
, which is known as the pseudo-hyperbolic distance between
$|\phi |$
, which is known as the pseudo-hyperbolic distance between
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
. We generalize such characterization to the weighted case and construct an example to illustrate the result.
$\psi $
. We generalize such characterization to the weighted case and construct an example to illustrate the result.
Theorem 3.5. Let
![]() $uC_{\varphi }$
and
$uC_{\varphi }$
and
![]() $vC_{\psi }$
be two weighted composition operators on
$vC_{\psi }$
be two weighted composition operators on
![]() $A^2_{\alpha }$
. Then the following statements are equivalent.
$A^2_{\alpha }$
. Then the following statements are equivalent.
-
(i) The operator
 $uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
$uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
 $A^2_{\alpha }$
.
$A^2_{\alpha }$
. -
(ii)
 $ {|\phi | u}/{(1 - |\varphi |^2)^{1 + {\alpha }/{2}}}, \, {v}/{(1 - |\psi |^2)^{1 + {\alpha }/{2}}} - {u(1 - |\psi |^2)^{1 + {\alpha }/{2}}}/{(1 - \overline {\psi }{\varphi })^{\alpha + 2}} \in L^2 (D, dA_{\alpha })$
.
$ {|\phi | u}/{(1 - |\varphi |^2)^{1 + {\alpha }/{2}}}, \, {v}/{(1 - |\psi |^2)^{1 + {\alpha }/{2}}} - {u(1 - |\psi |^2)^{1 + {\alpha }/{2}}}/{(1 - \overline {\psi }{\varphi })^{\alpha + 2}} \in L^2 (D, dA_{\alpha })$
. -
(iii)
 $ {|\phi | v}/{(1 - |\psi |^2)^{1 + {\alpha }/{2}}}, \, {u}/{(1 - |\varphi |^2)^{1 + {\alpha }/{2}}} - {v(1 - |\varphi |^2)^{1 + {\alpha }/{2}}}/{(1 - \overline {\varphi }{\psi })^{\alpha + 2}} \in L^2 (D, dA_{\alpha })$
.
$ {|\phi | v}/{(1 - |\psi |^2)^{1 + {\alpha }/{2}}}, \, {u}/{(1 - |\varphi |^2)^{1 + {\alpha }/{2}}} - {v(1 - |\varphi |^2)^{1 + {\alpha }/{2}}}/{(1 - \overline {\varphi }{\psi })^{\alpha + 2}} \in L^2 (D, dA_{\alpha })$
.
Proof. We first compute
![]() $\sum _{k=0}^{\infty } \|(uC_{\varphi } - vC_{\psi })e_k\|^2$
:
$\sum _{k=0}^{\infty } \|(uC_{\varphi } - vC_{\psi })e_k\|^2$
:
 $$ \begin{align*} & \sum_{k=0}^{\infty} \|(uC_{\varphi} - vC_{\psi})e_k\|^2 \\[6pt] &\quad = \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} \|u\varphi^k - v\psi^k\|^2 \\[6pt] &\quad = \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} \int_D |u\varphi^k - v\psi^k|^2\, dA_{\alpha} \\[6pt] &\quad = \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} \int_D [|u|^2|\varphi|^{2k} + |v|^2|\psi|^{2k} - 2\,{\textrm{Re}}(u\overline{v}(\varphi\overline{\psi})^k)] \, dA_{\alpha}. \end{align*} $$
$$ \begin{align*} & \sum_{k=0}^{\infty} \|(uC_{\varphi} - vC_{\psi})e_k\|^2 \\[6pt] &\quad = \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} \|u\varphi^k - v\psi^k\|^2 \\[6pt] &\quad = \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} \int_D |u\varphi^k - v\psi^k|^2\, dA_{\alpha} \\[6pt] &\quad = \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} \int_D [|u|^2|\varphi|^{2k} + |v|^2|\psi|^{2k} - 2\,{\textrm{Re}}(u\overline{v}(\varphi\overline{\psi})^k)] \, dA_{\alpha}. \end{align*} $$
Interchanging the summation and integral signs in the last equality is valid because all the terms
![]() ${\Gamma (\alpha + 2 + k)}/{k! \,\Gamma (\alpha + 2)}|u\varphi ^k - v\psi ^k|^2$
are nonnegative. Then
${\Gamma (\alpha + 2 + k)}/{k! \,\Gamma (\alpha + 2)}|u\varphi ^k - v\psi ^k|^2$
are nonnegative. Then
 $$ \begin{align*} & \sum_{k=0}^{\infty} \|(uC_{\varphi} - vC_{\psi})e_k\|^2 \\[6pt] &\quad = \int_D \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} [|u|^2|\varphi|^{2k} + |v|^2|\psi|^{2k} - 2\,{\textrm{Re}}(u\overline{v}(\varphi\overline{\psi})^k)] \, dA_{\alpha} \\[6pt] &\quad = \int_D \bigg[|u|^2 \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} |\varphi|^{2k} + |v|^2 \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} |\psi|^{2k} \\[6pt] & \quad\quad -2\,{\textrm{Re}}\bigg(u\overline{v}\sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)}(\varphi\overline{\psi})^k\bigg)\bigg]\, dA_{\alpha} \\[6pt] &\quad = \int_D \bigg[\frac{|u|^2}{(1 - |\varphi|^2)^{\alpha + 2}} + \frac{|v|^2}{(1 - |\psi|^2)^{\alpha + 2}} - 2\,{\textrm{Re}}\bigg(\frac{u\overline{v}}{(1 - \varphi\overline{\psi})^{\alpha + 2}}\bigg)\bigg]\, dA_{\alpha}. \end{align*} $$
$$ \begin{align*} & \sum_{k=0}^{\infty} \|(uC_{\varphi} - vC_{\psi})e_k\|^2 \\[6pt] &\quad = \int_D \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} [|u|^2|\varphi|^{2k} + |v|^2|\psi|^{2k} - 2\,{\textrm{Re}}(u\overline{v}(\varphi\overline{\psi})^k)] \, dA_{\alpha} \\[6pt] &\quad = \int_D \bigg[|u|^2 \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} |\varphi|^{2k} + |v|^2 \sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)} |\psi|^{2k} \\[6pt] & \quad\quad -2\,{\textrm{Re}}\bigg(u\overline{v}\sum_{k=0}^{\infty} \frac{\Gamma(\alpha + 2 + k)}{k! \,\Gamma(\alpha + 2)}(\varphi\overline{\psi})^k\bigg)\bigg]\, dA_{\alpha} \\[6pt] &\quad = \int_D \bigg[\frac{|u|^2}{(1 - |\varphi|^2)^{\alpha + 2}} + \frac{|v|^2}{(1 - |\psi|^2)^{\alpha + 2}} - 2\,{\textrm{Re}}\bigg(\frac{u\overline{v}}{(1 - \varphi\overline{\psi})^{\alpha + 2}}\bigg)\bigg]\, dA_{\alpha}. \end{align*} $$
Since
![]() $\varphi = (\psi - \phi ) / (1 - \overline {\psi }\phi )$
, it follows that
$\varphi = (\psi - \phi ) / (1 - \overline {\psi }\phi )$
, it follows that
 $$ \begin{align*} & \frac{|u|^2}{(1 - |\varphi|^2)^{\alpha + 2}} + \frac{|v|^2}{(1 - |\psi|^2)^{\alpha + 2}} - 2\,{\textrm{Re}}\bigg(\frac{u\overline{v}}{(1 - \varphi\overline{\psi})^{\alpha + 2}}\bigg) \\[3pt] &\quad = |u|^2\bigg[\frac{|1 - \overline{\psi}\phi|^2}{(1 - |\psi|^2)(1 - |\phi|^2)}\bigg]^{\alpha + 2} + \frac{|v|^2}{(1 - |\psi|^2)^{\alpha + 2}} - 2\,{\textrm{Re}}\bigg[u\overline{v}\bigg(\frac{1 - \overline{\psi}\phi}{1 - |\psi|^2}\bigg)^{\alpha + 2}\bigg] \\[3pt] &\quad = \frac{1}{(1 - |\psi|^2)^{\alpha + 2}}\bigg[|u|^2\bigg(\frac{|1 - \overline{\psi}\phi|^2}{1 - |\phi|^2}\bigg)^{\alpha + 2} + |v|^2 - 2\,{\textrm{Re}}(u\overline{v}(1 - \overline{\psi}\phi)^{\alpha + 2})\bigg] \\[3pt] &\quad = \frac{1}{(1 - |\psi|^2)^{\alpha + 2}}\bigg[|u|^2\bigg(\frac{|1 - \overline{\psi}\phi|^2}{1 - |\phi|^2}\bigg)^{\alpha + 2} + |v - u(1 - \overline{\psi}\phi)^{\alpha + 2}|^2 \ - |u|^2 |1 - \overline{\psi}\phi|^{2\alpha + 4}\bigg] \\[3pt] &\quad = \frac{1}{(1 - |\psi|^2)^{\alpha + 2}}\bigg[|u|^2\bigg(\frac{|1 - \overline{\psi}\phi|^2}{1 - |\phi|^2}\bigg)^{\alpha + 2}(1 - (1 - |\phi|^2)^{\alpha + 2}) \ + |v - u(1 - \overline{\psi}\phi)^{\alpha + 2}|^2\bigg] \\[3pt] &\quad = \frac{[1 - (1 - |\phi|^2)^{\alpha + 2}] |u|^2}{(1 - |\varphi|^2)^{\alpha + 2}} + \bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg|^2. \end{align*} $$
$$ \begin{align*} & \frac{|u|^2}{(1 - |\varphi|^2)^{\alpha + 2}} + \frac{|v|^2}{(1 - |\psi|^2)^{\alpha + 2}} - 2\,{\textrm{Re}}\bigg(\frac{u\overline{v}}{(1 - \varphi\overline{\psi})^{\alpha + 2}}\bigg) \\[3pt] &\quad = |u|^2\bigg[\frac{|1 - \overline{\psi}\phi|^2}{(1 - |\psi|^2)(1 - |\phi|^2)}\bigg]^{\alpha + 2} + \frac{|v|^2}{(1 - |\psi|^2)^{\alpha + 2}} - 2\,{\textrm{Re}}\bigg[u\overline{v}\bigg(\frac{1 - \overline{\psi}\phi}{1 - |\psi|^2}\bigg)^{\alpha + 2}\bigg] \\[3pt] &\quad = \frac{1}{(1 - |\psi|^2)^{\alpha + 2}}\bigg[|u|^2\bigg(\frac{|1 - \overline{\psi}\phi|^2}{1 - |\phi|^2}\bigg)^{\alpha + 2} + |v|^2 - 2\,{\textrm{Re}}(u\overline{v}(1 - \overline{\psi}\phi)^{\alpha + 2})\bigg] \\[3pt] &\quad = \frac{1}{(1 - |\psi|^2)^{\alpha + 2}}\bigg[|u|^2\bigg(\frac{|1 - \overline{\psi}\phi|^2}{1 - |\phi|^2}\bigg)^{\alpha + 2} + |v - u(1 - \overline{\psi}\phi)^{\alpha + 2}|^2 \ - |u|^2 |1 - \overline{\psi}\phi|^{2\alpha + 4}\bigg] \\[3pt] &\quad = \frac{1}{(1 - |\psi|^2)^{\alpha + 2}}\bigg[|u|^2\bigg(\frac{|1 - \overline{\psi}\phi|^2}{1 - |\phi|^2}\bigg)^{\alpha + 2}(1 - (1 - |\phi|^2)^{\alpha + 2}) \ + |v - u(1 - \overline{\psi}\phi)^{\alpha + 2}|^2\bigg] \\[3pt] &\quad = \frac{[1 - (1 - |\phi|^2)^{\alpha + 2}] |u|^2}{(1 - |\varphi|^2)^{\alpha + 2}} + \bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg|^2. \end{align*} $$
Therefore,
 $$ \begin{align*} & \sum_{k=0}^{\infty} \|(uC_{\varphi} - vC_{\psi})e_k\|^2 \\[3pt] &\quad = \int_D \bigg[\frac{(1 - (1 - |\phi|^2)^{\alpha + 2}) |u|^2}{(1 - |\varphi|^2)^{\alpha + 2}} + \bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg|^2\bigg]\, dA_{\alpha}. \end{align*} $$
$$ \begin{align*} & \sum_{k=0}^{\infty} \|(uC_{\varphi} - vC_{\psi})e_k\|^2 \\[3pt] &\quad = \int_D \bigg[\frac{(1 - (1 - |\phi|^2)^{\alpha + 2}) |u|^2}{(1 - |\varphi|^2)^{\alpha + 2}} + \bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg|^2\bigg]\, dA_{\alpha}. \end{align*} $$
The operator
![]() $uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
$uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
![]() $A^2_{\alpha }$
if and only if
$A^2_{\alpha }$
if and only if
 $$ \begin{align*}\frac{\sqrt{1 - (1 - |\phi|^2)^{\alpha + 2}} \, u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}}, \, \frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}} \in L^2(D, dA_{\alpha}). \end{align*} $$
$$ \begin{align*}\frac{\sqrt{1 - (1 - |\phi|^2)^{\alpha + 2}} \, u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}}, \, \frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}} \in L^2(D, dA_{\alpha}). \end{align*} $$
Moreover, write
 $$ \begin{align*}\frac{\sqrt{1 - (1 - |\phi|^2)^{\alpha + 2}} \, u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}} = \sqrt{\frac{1 - (1 - |\phi|^2)^{\alpha + 2}}{|\phi|^2}} \cdot \frac{|\phi| u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}}. \end{align*} $$
$$ \begin{align*}\frac{\sqrt{1 - (1 - |\phi|^2)^{\alpha + 2}} \, u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}} = \sqrt{\frac{1 - (1 - |\phi|^2)^{\alpha + 2}}{|\phi|^2}} \cdot \frac{|\phi| u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}}. \end{align*} $$
Note that the function
![]() $f(x) = [1 - (1 - x^2)^{\alpha + 2}] / x^2$
is continuous and positive on
$f(x) = [1 - (1 - x^2)^{\alpha + 2}] / x^2$
is continuous and positive on
![]() $(0, 1]$
. This, in conjunction with the fact
$(0, 1]$
. This, in conjunction with the fact
![]() $\lim _{x \to 0^+} f(x) = \alpha + 2> 0$
, implies that f is bounded above and away from zero on
$\lim _{x \to 0^+} f(x) = \alpha + 2> 0$
, implies that f is bounded above and away from zero on
![]() $(0, 1)$
. Thus,
$(0, 1)$
. Thus,
 $$ \begin{align*}\frac{\sqrt{1 - (1 - |\phi|^2)^{\alpha + 2}} \, u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}} \in L^2(D, dA_{\alpha}) \end{align*} $$
$$ \begin{align*}\frac{\sqrt{1 - (1 - |\phi|^2)^{\alpha + 2}} \, u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}} \in L^2(D, dA_{\alpha}) \end{align*} $$
if and only if
![]() $|\phi | u / (1 - |\varphi |^2)^{1 + {\alpha }/{2}} \in L^2(D, dA_{\alpha })$
. This establishes the equivalence of statements (i) and (ii).
$|\phi | u / (1 - |\varphi |^2)^{1 + {\alpha }/{2}} \in L^2(D, dA_{\alpha })$
. This establishes the equivalence of statements (i) and (ii).
Furthermore, upon switching the roles of
![]() $u, v$
and the roles of
$u, v$
and the roles of
![]() $\varphi , \psi $
in the preceding calculations, we obtain
$\varphi , \psi $
in the preceding calculations, we obtain
 $$ \begin{align*} & \sum_{k=0}^{\infty} \|(vC_{\psi} - uC_{\varphi})e_k\|^2 \\[3pt] &\quad = \int_D \bigg[\frac{(1 - (1 - |\phi|^2)^{\alpha + 2}) |v|^2}{(1 - |\psi|^2)^{\alpha + 2}} + \bigg|\frac{u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}} - \frac{v(1 - |\varphi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\varphi}{\psi})^{\alpha + 2}}\bigg|^2\bigg]\, dA_{\alpha}. \end{align*} $$
$$ \begin{align*} & \sum_{k=0}^{\infty} \|(vC_{\psi} - uC_{\varphi})e_k\|^2 \\[3pt] &\quad = \int_D \bigg[\frac{(1 - (1 - |\phi|^2)^{\alpha + 2}) |v|^2}{(1 - |\psi|^2)^{\alpha + 2}} + \bigg|\frac{u}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}} - \frac{v(1 - |\varphi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\varphi}{\psi})^{\alpha + 2}}\bigg|^2\bigg]\, dA_{\alpha}. \end{align*} $$
By a similar argument, statements (i) and (iii) are also equivalent.
Taking
![]() $v = 0$
and
$v = 0$
and
![]() $\varphi = \psi $
in the above theorem, we obtain the characterization in Equation (3-1) for a single Hilbert–Schmidt weighted composition operator. There are also two nontrivial consequences of Theorem 3.5. The first one characterizes the Hilbert–Schmidt difference of two composition operators on
$\varphi = \psi $
in the above theorem, we obtain the characterization in Equation (3-1) for a single Hilbert–Schmidt weighted composition operator. There are also two nontrivial consequences of Theorem 3.5. The first one characterizes the Hilbert–Schmidt difference of two composition operators on
![]() $A^2_{\alpha }$
. The second one, which generalizes [Reference Choe, Hosokawa and Koo2, Corollary 3.8], states that the Hilbert–Schmidt property of the difference of weighted composition operators on a smaller space extends to larger spaces.
$A^2_{\alpha }$
. The second one, which generalizes [Reference Choe, Hosokawa and Koo2, Corollary 3.8], states that the Hilbert–Schmidt property of the difference of weighted composition operators on a smaller space extends to larger spaces.
Corollary 3.6 [Reference Choe, Hosokawa and Koo2, Corollary 3.7].
The operator
![]() $C_{\varphi } - C_{\psi }$
is Hilbert–Schmidt on
$C_{\varphi } - C_{\psi }$
is Hilbert–Schmidt on
![]() $A^2_{\alpha }$
if and only if
$A^2_{\alpha }$
if and only if
 $$ \begin{align*}\frac{|\phi|}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}}, \, \frac{|\phi|}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} \in L^2(D, dA_{\alpha}). \end{align*} $$
$$ \begin{align*}\frac{|\phi|}{(1 - |\varphi|^2)^{1 + {\alpha}/{2}}}, \, \frac{|\phi|}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} \in L^2(D, dA_{\alpha}). \end{align*} $$
Proof. The ‘only if’ part is evident by taking
![]() $u = v = 1$
in Theorem 3.5. To prove the ‘if’ part, assume that both
$u = v = 1$
in Theorem 3.5. To prove the ‘if’ part, assume that both
![]() $|\phi | / (1 - |\varphi |^2)^{1 + {\alpha }/{2}}$
and
$|\phi | / (1 - |\varphi |^2)^{1 + {\alpha }/{2}}$
and
![]() $|\phi | / (1 - |\psi |^2)^{1 + {\alpha }/{2}}$
are in
$|\phi | / (1 - |\psi |^2)^{1 + {\alpha }/{2}}$
are in
![]() $L^2(D, dA_{\alpha })$
. Write
$L^2(D, dA_{\alpha })$
. Write
 $$ \begin{align*} &\frac{1}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}} = \frac{1 - (1 - \overline{\psi}{\phi})^{\alpha + 2}}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} \\[3pt] &\quad = \frac{1 - (1 - \overline{\psi}{\phi})^{\alpha + 2}}{\phi} \cdot \frac{\phi}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}. \end{align*} $$
$$ \begin{align*} &\frac{1}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}} = \frac{1 - (1 - \overline{\psi}{\phi})^{\alpha + 2}}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} \\[3pt] &\quad = \frac{1 - (1 - \overline{\psi}{\phi})^{\alpha + 2}}{\phi} \cdot \frac{\phi}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}. \end{align*} $$
By the continuity of the function
![]() $g(z) = [1 - (1 - \overline {w}{z})^{\alpha + 2}] / z$
(
$g(z) = [1 - (1 - \overline {w}{z})^{\alpha + 2}] / z$
(
![]() $w \in D$
) on
$w \in D$
) on
![]() $D \setminus \{0\}$
and the fact that
$D \setminus \{0\}$
and the fact that
![]() $\lim _{z \to 0} g(z)$
exists (and equals
$\lim _{z \to 0} g(z)$
exists (and equals
![]() $(\alpha + 2)\overline {w}$
), the expression
$(\alpha + 2)\overline {w}$
), the expression
![]() $[1 - (1 - \overline {\psi }{\phi })^{\alpha + 2}] / \phi $
is bounded on the set
$[1 - (1 - \overline {\psi }{\phi })^{\alpha + 2}] / \phi $
is bounded on the set
![]() $\{z \in D : \phi (z) \ne 0\}$
. Thus,
$\{z \in D : \phi (z) \ne 0\}$
. Thus,
 $$ \begin{align*}\frac{1}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}} \in L^2(D, dA_{\alpha}) \end{align*} $$
$$ \begin{align*}\frac{1}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}} \in L^2(D, dA_{\alpha}) \end{align*} $$
as well. In light of Theorem 3.5,
![]() $C_{\varphi } - C_{\psi }$
is Hilbert–Schmidt on
$C_{\varphi } - C_{\psi }$
is Hilbert–Schmidt on
![]() $A^2_{\alpha }$
.
$A^2_{\alpha }$
.
Corollary 3.7. Let
![]() $uC_{\varphi }$
and
$uC_{\varphi }$
and
![]() $vC_{\psi }$
be two weighted composition operators on
$vC_{\psi }$
be two weighted composition operators on
![]() $A^2_{\alpha }$
. If
$A^2_{\alpha }$
. If
![]() $uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
$uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
![]() $A^2_{\alpha }$
, then
$A^2_{\alpha }$
, then
![]() $uC_{\varphi } - vC_{\psi }$
is also Hilbert–Schmidt on
$uC_{\varphi } - vC_{\psi }$
is also Hilbert–Schmidt on
![]() $A^2_{\beta }$
for every
$A^2_{\beta }$
for every
![]() $\beta> \alpha > -1$
.
$\beta> \alpha > -1$
.
Proof. Since
![]() $uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
$uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
![]() $A^2_{\alpha }$
, the following functions are all in
$A^2_{\alpha }$
, the following functions are all in
![]() $L^2(D, d\tau )$
, where
$L^2(D, d\tau )$
, where
![]() $\tau $
is the measure defined in Equation (3-5):
$\tau $
is the measure defined in Equation (3-5):
-
(i)
 $ |\phi | u (({1 - |z|^2})/({1 - |\varphi |^2}))^{1 + {\alpha }/{2}}$
;
$ |\phi | u (({1 - |z|^2})/({1 - |\varphi |^2}))^{1 + {\alpha }/{2}}$
; -
(ii)
 $ |\phi | v (({1 - |z|^2})/({1 - |\psi |^2}))^{1 + {\alpha }/{2}}$
;
$ |\phi | v (({1 - |z|^2})/({1 - |\psi |^2}))^{1 + {\alpha }/{2}}$
; -
(iii)
 $ [{v}/{(1 - |\psi |^2)^{1 + {\alpha }/{2}}} - {u(1 - |\psi |^2)^{1 + {\alpha }/{2}}}/{(1 - \overline {\psi }{\varphi })^{\alpha + 2}}](1 - |z|^2)^{1 + {\alpha }/{2}}$
;
$ [{v}/{(1 - |\psi |^2)^{1 + {\alpha }/{2}}} - {u(1 - |\psi |^2)^{1 + {\alpha }/{2}}}/{(1 - \overline {\psi }{\varphi })^{\alpha + 2}}](1 - |z|^2)^{1 + {\alpha }/{2}}$
;
since
 $$ \begin{align} \bigg(\frac{1 - |z|}{1 - |\varphi|}\bigg)^{\beta - \alpha} \leq \bigg(\frac{1 + |\varphi(0)|}{1 - |\varphi(0)|}\bigg)^{\beta - \alpha} \end{align} $$
$$ \begin{align} \bigg(\frac{1 - |z|}{1 - |\varphi|}\bigg)^{\beta - \alpha} \leq \bigg(\frac{1 + |\varphi(0)|}{1 - |\varphi(0)|}\bigg)^{\beta - \alpha} \end{align} $$
[Reference Cowen and MacCluer3, page 48] and
 $$ \begin{align} \frac{1}{2}\bigg(\frac{1 - |z|}{1 - |\varphi|}\bigg) \leq \frac{1 - |z|^2}{1 - |\varphi|^2} \leq 2\bigg(\frac{1 - |z|}{1 - |\varphi|}\bigg) \end{align} $$
$$ \begin{align} \frac{1}{2}\bigg(\frac{1 - |z|}{1 - |\varphi|}\bigg) \leq \frac{1 - |z|^2}{1 - |\varphi|^2} \leq 2\bigg(\frac{1 - |z|}{1 - |\varphi|}\bigg) \end{align} $$
(both Equations (3-6) and (3-7) hold if
![]() $\varphi $
is replaced by
$\varphi $
is replaced by
![]() $\psi $
), we have
$\psi $
), we have
 $$ \begin{align*} & \int_D |\phi|^2 |u|^2 \bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2}\, d\tau(z) \\[3pt] &\quad \leq 2^{\alpha + \beta + 4}\bigg(\frac{1 + |\varphi(0)|}{1 - |\varphi(0)|}\bigg)^{\beta - \alpha}\int_D |\phi|^2 |u|^2 \bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\alpha + 2}\, d\tau(z)\\[3pt] &\quad < \infty. \end{align*} $$
$$ \begin{align*} & \int_D |\phi|^2 |u|^2 \bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2}\, d\tau(z) \\[3pt] &\quad \leq 2^{\alpha + \beta + 4}\bigg(\frac{1 + |\varphi(0)|}{1 - |\varphi(0)|}\bigg)^{\beta - \alpha}\int_D |\phi|^2 |u|^2 \bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\alpha + 2}\, d\tau(z)\\[3pt] &\quad < \infty. \end{align*} $$
From the proof of Corollary 3.6,
 $$ \begin{align*} & \bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\beta}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg|^2 \\[3pt] &\quad = \bigg|v\bigg[\frac{1}{(1 - |\psi|^2)^{1 + {\beta}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg] + (v - u)\frac{(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg|^2 \\[3pt] &\quad \leq 2\bigg[\bigg|\frac{1 - (1 - \overline{\psi}{\phi})^{\,\beta + 2}}{\phi}\bigg|^2 \frac{|\phi|^2 |v|^2}{(1 - |\psi|^2)^{\,\beta + 2}} + |v-u|^2 \frac{(1 - |\psi|^2)^{\,\beta + 2}}{|1 - \overline{\psi}{\varphi}|^{2\beta + 4}}\bigg] \\[3pt] &\quad \leq 2\bigg[M_{\beta} \frac{|\phi|^2 |v|^2}{(1 - |\psi|^2)^{\,\beta + 2}} + |v - u|^2 \bigg(\frac{1 - |\phi|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2}\bigg], \end{align*} $$
$$ \begin{align*} & \bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\beta}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg|^2 \\[3pt] &\quad = \bigg|v\bigg[\frac{1}{(1 - |\psi|^2)^{1 + {\beta}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg] + (v - u)\frac{(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg|^2 \\[3pt] &\quad \leq 2\bigg[\bigg|\frac{1 - (1 - \overline{\psi}{\phi})^{\,\beta + 2}}{\phi}\bigg|^2 \frac{|\phi|^2 |v|^2}{(1 - |\psi|^2)^{\,\beta + 2}} + |v-u|^2 \frac{(1 - |\psi|^2)^{\,\beta + 2}}{|1 - \overline{\psi}{\varphi}|^{2\beta + 4}}\bigg] \\[3pt] &\quad \leq 2\bigg[M_{\beta} \frac{|\phi|^2 |v|^2}{(1 - |\psi|^2)^{\,\beta + 2}} + |v - u|^2 \bigg(\frac{1 - |\phi|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2}\bigg], \end{align*} $$
where
![]() $M_{\beta }$
is a constant depending on
$M_{\beta }$
is a constant depending on
![]() $\beta $
only. Then
$\beta $
only. Then
 $$ \begin{align*} & \bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\beta}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg|^2 (1 - |z|^2)^{\,\beta + 2} \\[3pt] &\quad \leq 2\bigg[M_{\beta} |\phi|^2 |v|^2 \bigg(\frac{1 - |z|^2}{1 - |\psi|^2}\bigg)^{\,\beta + 2} + (1 - |\phi|^2)^{\,\beta + 2}|v - u|^2\bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2}\bigg]. \end{align*} $$
$$ \begin{align*} & \bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\beta}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg|^2 (1 - |z|^2)^{\,\beta + 2} \\[3pt] &\quad \leq 2\bigg[M_{\beta} |\phi|^2 |v|^2 \bigg(\frac{1 - |z|^2}{1 - |\psi|^2}\bigg)^{\,\beta + 2} + (1 - |\phi|^2)^{\,\beta + 2}|v - u|^2\bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2}\bigg]. \end{align*} $$
Note that
 $$ \begin{align} & \int_D |\phi|^2 |v|^2 \bigg(\frac{1 - |z|^2}{1 - |\psi|^2}\bigg)^{\,\beta + 2}\, d\tau(z) \nonumber \\[3pt] &\quad \leq 2^{\alpha + \beta + 4}\bigg(\frac{1 + |\psi(0)|}{1 - |\psi(0)|}\bigg)^{\beta - \alpha}\int_D |\phi|^2 |v|^2 \bigg(\frac{1 - |z|^2}{1 - |\psi|^2}\bigg)^{\alpha + 2}\, d\tau(z) \nonumber \\[3pt] &\quad < \infty. \end{align} $$
$$ \begin{align} & \int_D |\phi|^2 |v|^2 \bigg(\frac{1 - |z|^2}{1 - |\psi|^2}\bigg)^{\,\beta + 2}\, d\tau(z) \nonumber \\[3pt] &\quad \leq 2^{\alpha + \beta + 4}\bigg(\frac{1 + |\psi(0)|}{1 - |\psi(0)|}\bigg)^{\beta - \alpha}\int_D |\phi|^2 |v|^2 \bigg(\frac{1 - |z|^2}{1 - |\psi|^2}\bigg)^{\alpha + 2}\, d\tau(z) \nonumber \\[3pt] &\quad < \infty. \end{align} $$
Moreover, if we put
![]() $c = 2^{\alpha + \beta + 4}(({1 + |\varphi (0)|})/({1 - |\varphi (0)|}))^{\beta - \alpha }$
, then appealing to the proof of Corollary 3.6 again gives
$c = 2^{\alpha + \beta + 4}(({1 + |\varphi (0)|})/({1 - |\varphi (0)|}))^{\beta - \alpha }$
, then appealing to the proof of Corollary 3.6 again gives
 $$ \begin{align*} & (1 - |\phi|^2)^{\,\beta + 2}|v - u|^2\bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2} \\[3pt] &\quad \leq c(1 - |\phi|^2)^{\alpha + 2}|v - u|^2\bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\alpha + 2} \\[3pt] &\quad = c\bigg|v\bigg[\frac{1}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg] + (v - u)\frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}} \\[3pt] & \quad\quad -v\bigg[\frac{1}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg]\bigg|^2 (1 - |z|^2)^{\alpha + 2} \\[3pt] &\quad \leq 2c\bigg[\bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg|^2 \\[3pt] & \quad\quad +\bigg|\frac{1 - (1 - \overline{\psi}{\phi})^{\alpha + 2}}{\phi}\bigg|^2 \frac{|\phi|^2 |v|^2}{(1 - |\psi|^2)^{\alpha + 2}}\bigg](1 - |z|^2)^{\alpha + 2} \\[3pt] &\quad \leq 2c\bigg[\bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg|^2(1 - |z|^2)^{\alpha + 2} \\[3pt] & \quad\quad + M_{\alpha} |\phi|^2 |v|^2 \bigg(\frac{1 - |z|^2}{1 - |\psi|^2}\bigg)^{\alpha + 2}\bigg], \end{align*} $$
$$ \begin{align*} & (1 - |\phi|^2)^{\,\beta + 2}|v - u|^2\bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2} \\[3pt] &\quad \leq c(1 - |\phi|^2)^{\alpha + 2}|v - u|^2\bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\alpha + 2} \\[3pt] &\quad = c\bigg|v\bigg[\frac{1}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg] + (v - u)\frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}} \\[3pt] & \quad\quad -v\bigg[\frac{1}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg]\bigg|^2 (1 - |z|^2)^{\alpha + 2} \\[3pt] &\quad \leq 2c\bigg[\bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg|^2 \\[3pt] & \quad\quad +\bigg|\frac{1 - (1 - \overline{\psi}{\phi})^{\alpha + 2}}{\phi}\bigg|^2 \frac{|\phi|^2 |v|^2}{(1 - |\psi|^2)^{\alpha + 2}}\bigg](1 - |z|^2)^{\alpha + 2} \\[3pt] &\quad \leq 2c\bigg[\bigg|\frac{v}{(1 - |\psi|^2)^{1 + {\alpha}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi}{\varphi})^{\alpha + 2}}\bigg|^2(1 - |z|^2)^{\alpha + 2} \\[3pt] & \quad\quad + M_{\alpha} |\phi|^2 |v|^2 \bigg(\frac{1 - |z|^2}{1 - |\psi|^2}\bigg)^{\alpha + 2}\bigg], \end{align*} $$
where
![]() $M_{\alpha }$
is a constant depending on
$M_{\alpha }$
is a constant depending on
![]() $\alpha $
only. Thus,
$\alpha $
only. Thus,
 $$ \begin{align*}\int_D (1 - |\phi|^2)^{\,\beta + 2}|v - u|^2\bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2}\, d\tau(z) < \infty. \end{align*} $$
$$ \begin{align*}\int_D (1 - |\phi|^2)^{\,\beta + 2}|v - u|^2\bigg(\frac{1 - |z|^2}{1 - |\varphi|^2}\bigg)^{\,\beta + 2}\, d\tau(z) < \infty. \end{align*} $$
This, in conjunction with Equation (3-8), implies that
 $$ \begin{align*}\bigg[\frac{v}{(1 - |\psi|^2)^{1 + {\beta}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg](1 - |z|^2)^{1 + {\beta}/{2}}\in L^2(D, d\tau). \end{align*} $$
$$ \begin{align*}\bigg[\frac{v}{(1 - |\psi|^2)^{1 + {\beta}/{2}}} - \frac{u(1 - |\psi|^2)^{1 + {\beta}/{2}}}{(1 - \overline{\psi}{\varphi})^{\,\beta + 2}}\bigg](1 - |z|^2)^{1 + {\beta}/{2}}\in L^2(D, d\tau). \end{align*} $$
According to Theorem 3.5,
![]() $uC_{\varphi } - vC_{\psi }$
is also Hilbert–Schmidt on
$uC_{\varphi } - vC_{\psi }$
is also Hilbert–Schmidt on
![]() $A^2_{\beta }$
.
$A^2_{\beta }$
.
Example 3.8. Let
![]() $u(z) = v(z) = z$
,
$u(z) = v(z) = z$
,
![]() $\varphi (z) = az + 1 - a$
and
$\varphi (z) = az + 1 - a$
and
![]() $\psi (z) = \varphi (z) + \varepsilon (1 - \varphi (z))^b$
, where a, b,
$\psi (z) = \varphi (z) + \varepsilon (1 - \varphi (z))^b$
, where a, b,
![]() $\varepsilon $
are positive constants such that
$\varepsilon $
are positive constants such that
![]() $a \leq 1/2$
,
$a \leq 1/2$
,
![]() $b> 2$
, and
$b> 2$
, and
![]() $\varepsilon $
is to be determined. Since
$\varepsilon $
is to be determined. Since
![]() ${\textrm{Re}} (z) < 1$
for
${\textrm{Re}} (z) < 1$
for
![]() $z \in D$
, we have
$z \in D$
, we have
 $$ \begin{align*} 1 - |\varphi(z)|^2 - |1 - \varphi(z)|^2 & = 2a - 2a^2 - 2a^2|z|^2 + 2a(2a - 1){\textrm{Re}}(z) \\[3pt] & \geq 2a - 2a^2 - 2a^2|z|^2 + 2a(2a - 1) \\[3pt] & = 2a^2(1 - |z|^2) \\[3pt] &> 0, \end{align*} $$
$$ \begin{align*} 1 - |\varphi(z)|^2 - |1 - \varphi(z)|^2 & = 2a - 2a^2 - 2a^2|z|^2 + 2a(2a - 1){\textrm{Re}}(z) \\[3pt] & \geq 2a - 2a^2 - 2a^2|z|^2 + 2a(2a - 1) \\[3pt] & = 2a^2(1 - |z|^2) \\[3pt] &> 0, \end{align*} $$
that is,
Note that
![]() $0 < |1 - \varphi (z)| = a|1-z| < 1$
on D. In what follows, we choose
$0 < |1 - \varphi (z)| = a|1-z| < 1$
on D. In what follows, we choose
![]() $\varepsilon < 1/4$
. Then
$\varepsilon < 1/4$
. Then
 $$ \begin{align*} 1 - |\psi(z)|^2 &> 1 - |\varphi(z)|^2 - 2\varepsilon |1 - \varphi(z)|^b - \varepsilon^2 |1 - \varphi(z)|^{2b} \\[3pt] & > (1 - 2\varepsilon - \varepsilon^2)|1 - \varphi(z)|^2 \\[3pt] & > \tfrac{7}{16}a^2|1 - z|^2 \\[3pt] & > 0, \end{align*} $$
$$ \begin{align*} 1 - |\psi(z)|^2 &> 1 - |\varphi(z)|^2 - 2\varepsilon |1 - \varphi(z)|^b - \varepsilon^2 |1 - \varphi(z)|^{2b} \\[3pt] & > (1 - 2\varepsilon - \varepsilon^2)|1 - \varphi(z)|^2 \\[3pt] & > \tfrac{7}{16}a^2|1 - z|^2 \\[3pt] & > 0, \end{align*} $$
or
![]() $\psi (D) \subset D$
. We claim that
$\psi (D) \subset D$
. We claim that
![]() $uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
$uC_{\varphi } - vC_{\psi }$
is Hilbert–Schmidt on
![]() $A^2_{\alpha }$
if
$A^2_{\alpha }$
if
![]() ${3\alpha }/{4} + \tfrac 72 < b < {5\alpha }/{4} + \tfrac 92$
. Since
${3\alpha }/{4} + \tfrac 72 < b < {5\alpha }/{4} + \tfrac 92$
. Since
 $$ \begin{align*} |1 - \overline{\psi(z)}\varphi(z)| & = |1 - |\psi(z)|^2 + \overline{\psi(z)}(\psi(z) - \varphi(z))| \\[3pt] & \geq 1 - |\psi(z)|^2 - \varepsilon|1 - \varphi(z)|^b \\[3pt] &> \tfrac{7}{16}a^2|1 - z|^2 - \tfrac{1}{4}a^2|1 - z|^2 \\[3pt] & = \tfrac{3}{16}a^2|1 - z|^2, \end{align*} $$
$$ \begin{align*} |1 - \overline{\psi(z)}\varphi(z)| & = |1 - |\psi(z)|^2 + \overline{\psi(z)}(\psi(z) - \varphi(z))| \\[3pt] & \geq 1 - |\psi(z)|^2 - \varepsilon|1 - \varphi(z)|^b \\[3pt] &> \tfrac{7}{16}a^2|1 - z|^2 - \tfrac{1}{4}a^2|1 - z|^2 \\[3pt] & = \tfrac{3}{16}a^2|1 - z|^2, \end{align*} $$
we have
 $$ \begin{align*}|\phi(z)| = \bigg|\frac{\psi(z) - \varphi(z)}{1 - \overline{\psi(z)}\varphi(z)}\bigg| < \frac{16\varepsilon|1 - \varphi(z)|^b}{3a^2|1 - z|^2} < \frac{4}{3}a^{b-2}|1 - z|^{b-2}. \end{align*} $$
$$ \begin{align*}|\phi(z)| = \bigg|\frac{\psi(z) - \varphi(z)}{1 - \overline{\psi(z)}\varphi(z)}\bigg| < \frac{16\varepsilon|1 - \varphi(z)|^b}{3a^2|1 - z|^2} < \frac{4}{3}a^{b-2}|1 - z|^{b-2}. \end{align*} $$
Thus,
 $$ \begin{align*}\int_D \frac{|\phi(z)|^2 |u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) \leq M_1 \int_D \frac{1}{|1 - z|^{8 - 2b + 2\alpha}} \, dA_{\alpha}(z); \end{align*} $$
$$ \begin{align*}\int_D \frac{|\phi(z)|^2 |u(z)|^2}{(1 - |\varphi(z)|^2)^{\alpha + 2}} \, dA_{\alpha}(z) \leq M_1 \int_D \frac{1}{|1 - z|^{8 - 2b + 2\alpha}} \, dA_{\alpha}(z); \end{align*} $$
and from the proof of Corollary 3.6,
 $$ \begin{align*} & \int_D \bigg|\frac{v(z)}{(1 - |\psi(z)|^2)^{1 + {\alpha}/{2}}} - \frac{u(z)(1 - |\psi(z)|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi(z)}{\varphi(z)})^{\alpha + 2}}\bigg|^2\, dA_{\alpha}(z) \\[3pt] &\quad = \int_D \bigg|\frac{1 - (1 - \overline{\psi(z)}\phi(z))^{\alpha + 2}}{\phi(z)}\bigg|^2 \frac{|\phi(z)|^2 |z|^2}{(1 - |\psi(z)|^2)^{\alpha + 2}}\, dA_{\alpha}(z) \\[3pt] &\quad \leq M_2\int_D \frac{1}{|1 - z|^{8 - 2b + 2\alpha}} \, dA_{\alpha}(z), \end{align*} $$
$$ \begin{align*} & \int_D \bigg|\frac{v(z)}{(1 - |\psi(z)|^2)^{1 + {\alpha}/{2}}} - \frac{u(z)(1 - |\psi(z)|^2)^{1 + {\alpha}/{2}}}{(1 - \overline{\psi(z)}{\varphi(z)})^{\alpha + 2}}\bigg|^2\, dA_{\alpha}(z) \\[3pt] &\quad = \int_D \bigg|\frac{1 - (1 - \overline{\psi(z)}\phi(z))^{\alpha + 2}}{\phi(z)}\bigg|^2 \frac{|\phi(z)|^2 |z|^2}{(1 - |\psi(z)|^2)^{\alpha + 2}}\, dA_{\alpha}(z) \\[3pt] &\quad \leq M_2\int_D \frac{1}{|1 - z|^{8 - 2b + 2\alpha}} \, dA_{\alpha}(z), \end{align*} $$
where
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are positive constants depending on a, b, and
$M_2$
are positive constants depending on a, b, and
![]() $\alpha $
. The integral
$\alpha $
. The integral
![]() $\int _D ({1}/{|1 - z|^{8 - 2b + 2\alpha }}) \, dA_{\alpha }(z)$
is finite if and only if
$\int _D ({1}/{|1 - z|^{8 - 2b + 2\alpha }}) \, dA_{\alpha }(z)$
is finite if and only if
![]() $|8 - 2b + 2\alpha | < 1 + {\alpha }/{2}$
, that is,
$|8 - 2b + 2\alpha | < 1 + {\alpha }/{2}$
, that is,
![]() ${3\alpha }/{4} + \tfrac 72 < b < {5\alpha }/{4} + \tfrac 92$
. The claim now follows from Theorem 3.5.
${3\alpha }/{4} + \tfrac 72 < b < {5\alpha }/{4} + \tfrac 92$
. The claim now follows from Theorem 3.5.
Acknowledgment
The authors would like to thank the anonymous referee for his/her careful reading of the manuscript and helpful suggestions, which have improved the clarity of this paper.