Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T13:18:33.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Commutative rings with comparable regular elements

Part of: General commutative ring theory Arithmetic rings and other special rings

Published online by Cambridge University Press:  09 April 2009

Paolo Zanardo
Paolo Zanardo
Affiliation:
Dipartimento di Matematica Pura e ApplicataVia Belzoni 7 35131 PadovaItaly e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℜ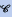 be the class of commutative rings R with comparable regular elements, that is, given two non zero-divisors in R, one divides the other. Applying the notion of V-valuation due to Harrison and Vitulli, we define the class V-val of V-valuated rings, which is contained in ℜ 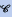and contains the class of Manis valuation rings. We prove that these inclusions of classes are both proper. We investigate Prüfer rings inside ℜ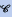, showing that there exist Prüfer rings which lie in ℜ 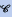but not in V-val; we prove that a ring R is a Prüfer valuation ring if and only if it is Prüfer and V-valuated, if and only if its lattice of regular ideals is a chain. Finally, we introduce and investigate the ideal I∞ of a ring R ∈ ℜ, which corresponds to the counterimage of ∞, whenever R is V-valuated.

MSC classification

Secondary: 13A18: Valuations and their generalizations 13F30: Valuation rings
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 60 , Issue 1 , February 1996 , pp. 90 - 108
Copyright
Copyright © Australian Mathematical Society 1996

References

[1]Alajbegovic, J. and Zanardo, P., ‘Uniserial modules over manis rings’, Comm. Algebra 17 (1989), 1463–1476.CrossRefGoogle Scholar
[2]Anderson, D. D. and Pascual, J., ‘Regular ideals in commutative rings, sublattices of regular ideals, and Prüfer rings’, J. Algebra 111 (1987), 404–426.Google Scholar
[3]Gräter, J., ‘An integrally closed ring which is not the intersection of valuation rings’, Proc. Amer. Math. Soc. 107 (1989), 333–336.Google Scholar
[4]Harrison, D. K. and Vitulli, M. A., ‘V-valuations of a commutative ring’, J. Algebra 126 (1989), 264–292.CrossRefGoogle Scholar
[5]Harrison, D. K. and Vitulli, M. A., ‘Complex-valued places and cmc subsets of a field’, Comm. Algebra 17 (1989), 2529–2537.Google Scholar
[6]Harrison, D. K. and Vitulli, M. A., ‘A categorical approach to the theory of equations’, J. Pure Appl. Algebra. 67 (1990), 15–31.CrossRefGoogle Scholar
[7]Huckaba, J. A., Commutative rings with zero divisors (Marcel Dekker, New York, 1988).Google Scholar
[8]Lucas, T. G., ‘Valuation rings and integral closure’, Canad. Math. Bull. 33 (1990), 327–330.Google Scholar
[9]Krull, W., ‘Allgemeine Bewertungstheorie’, J. Reine Angew. Math. 167 (1932), 160–196.Google Scholar
[10]Manis, M., ‘Valuations on a commutative ring’, Proc. Amer. Math. Soc. 20 (1969), 193–198.Google Scholar
[11]Marcus, D. A., Number fields (Springer, New York, 1977).Google Scholar
[12]Marot, J., ‘Extension de la notion d'anneau valuation’, Dept. Math. Faculté Sci. de Brest (1968).Google Scholar
[13]Nagata, M., Local rings (Wiley, Interscience, New York, 1962).Google Scholar
[14]Samuel, P., ‘La notion de place dans un anneau’, Bull. Soc. Math. France 85 (1957), 123–133.CrossRefGoogle Scholar
[15]Silverman, J. H., The arithmetic of elliptic curves (Springer, New York, 1986).Google Scholar
[16]Zanardo, P., ‘Constructions of Manis valuation rings’, Comm. Algebra 21 (1993), 4183–4194.CrossRefGoogle Scholar