Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Odlyzko, A. M.
1981.
On the ranks of some (0, 1)-matrices with constant row sums.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 31,
Issue. 2,
p.
193.
Ahlswede, R.
Aydinian, H.
and
Khachatrian, L.H.
2001.
Extremal problems under dimension constraints.
Electronic Notes in Discrete Mathematics,
Vol. 10,
Issue. ,
p.
154.
Ahlswede, R.
Aydinian, H.
and
Khachatrian, L.H.
2003.
Extremal problems under dimension constraints.
Discrete Mathematics,
Vol. 273,
Issue. 1-3,
p.
9.
Grosu, Codruţ
Person, Yury
and
Szabó, Tibor
2014.
On the rank of higher inclusion matrices.
Journal of the London Mathematical Society,
Vol. 90,
Issue. 2,
p.
333.
Penz, Markus
and
van Leeuwen, Robert
2021.
Density-functional theory on graphs.
The Journal of Chemical Physics,
Vol. 155,
Issue. 24,


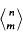 denote the least integer
denote the least integer 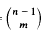 +1 for
+1 for 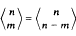 for 1 ≦ m < n.
for 1 ≦ m < n.