No CrossRef data available.
Published online by Cambridge University Press: 09 April 2009
Let A denote the set of all functions analytic in U = {z: |;z| < 1} equipped with the topology of unifrom convergence on compact subsets of U. For F ∈ A define 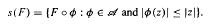 Let
Let 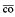 s(F) and
s(F) and 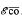 s(F) denote the closed convex hull of s(F) and the set of extreme points of
s(F) denote the closed convex hull of s(F) and the set of extreme points of 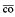 , respectively. Let R denote the class of all F ∈ A such that
, respectively. Let R denote the class of all F ∈ A such that 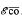 = {Fx}: |x| = 1} where Fx = F(xz).
= {Fx}: |x| = 1} where Fx = F(xz).
We prove that |An| ≤ |AMN| for all positive integers M and N, and 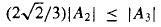 for
for 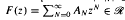 . We also prove that if
. We also prove that if 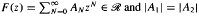 , then F is a univelaent halfplane mapping.
, then F is a univelaent halfplane mapping.