Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T05:24:21.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficients for the study of Runge-Kutta integration processes

Published online by Cambridge University Press:  09 April 2009

J. C. Butcher
J. C. Butcher
Affiliation:
Department of Mathematics, University of Canterbury, Christchurch, New Zealand.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

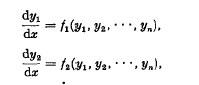
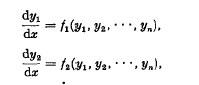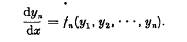We consider a set of η first order simultaneous differential equations in the dependent variables y1, y2, …, yn and the independent variable x ⋮ No loss of gernerality results from taking the functions f1, f2, …, fn to be independent of x, for if this were not so an additional dependent variable yn+1, anc be introduced which always equals x and thus satisfies the differential equation

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 3 , Issue 2 , May 1963 , pp. 185 - 201
Copyright
Copyright © Australian Mathematical Society 1963

References

[1]Runge, C., Über die numerische Auflösung von Differentialgleichungen. Math. Ann. 46 (1895), 167–178.CrossRefGoogle Scholar
[2]Kutta, W., Beitrag zur näherungsweisen Integration totaler Differentialgleichungen. Zeit. Math. Physik, 46 (1901), 435–452.Google Scholar
[3]Nyström, E. J., Über die numerische Integration von Differentialgleichungen. Acta Soc. Sci. Fennicae 50, No. 13 (1925).Google Scholar
[4]Gill, S., A process for the step-by-step Integration of Differential Equations in an Automatic Digital Computing Machine. Proc. Camb. Phil. Soc. 47 (1951), 96–108.CrossRefGoogle Scholar
[5]Merson, R. H., An operational method for the study of integration processes. Proceedings of conference on data processing and Automatic Computing Machines at Weapons Research Establishment, Salisbury, South Australia (1957).Google Scholar
[6]Polya, G. and Szegö, G., Aufgaben und Lehrsätze aus der Analysis I, p. 301. Grind. Math. Wiss. 19 (Springer, 1925).Google Scholar