Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T01:02:08.744Z Has data issue: false hasContentIssue false
  • English
  • Français

COEFFICIENT INEQUALITIES AND YAMASHITA’S CONJECTURE FOR SOME CLASSES OF ANALYTIC FUNCTIONS

Part of: Geometric function theory

Published online by Cambridge University Press:  29 September 2015

MD FIROZ ALI  and
A. VASUDEVARAO
MD FIROZ ALI*
Affiliation:
Department of Mathematics, IIT Kharagpur, Kharagpur-721 302, West Bengal, India email [email protected]
A. VASUDEVARAO
Affiliation:
Department of Mathematics, IIT Kharagpur, Kharagpur-721 302, West Bengal, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any real number 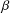${\it\beta}$ with 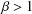${\it\beta}>1$, let 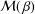${\mathcal{M}}(\,{\it\beta})$ (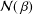${\mathcal{N}}(\,{\it\beta})$ respectively) denote the class of analytic functions 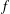$f$ in the unit disk 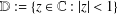$\mathbb{D}:=\{z\in \mathbb{C}:|z|<1\}$ of the form 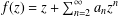$f(z)=z+\sum _{n=2}^{\infty }a_{n}z^{n}$ and satisfying 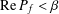$\text{Re}\,P_{f}<{\it\beta}$ (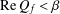$\text{Re}\,Q_{f}<{\it\beta}$ respectively) in 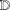$\mathbb{D}$, where 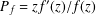$P_{f}=zf^{\prime }(z)/f(z)$ and 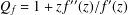$Q_{f}=1+zf^{\prime \prime }(z)/f^{\prime }(z)$. Also, for 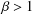${\it\beta}>1$, let 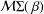${\mathcal{M}}{\rm\Sigma}(\,{\it\beta})$ (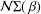${\mathcal{N}}{\rm\Sigma}(\,{\it\beta})$ respectively) denote the class of analytic functions 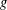$g$ of the form 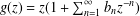$g(z)=z(1+\sum _{n=1}^{\infty }b_{n}z^{-n})$ and satisfying 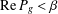$\text{Re}\,P_{g}<{\it\beta}$ (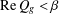$\text{Re}\,Q_{g}<{\it\beta}$ respectively) for 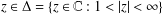$z\in {\rm\Delta}=\{z\in \mathbb{C}:1<|z|<\infty \}$. In this paper, we shall determine the coefficient bounds, inverse coefficient bounds, the growth and distortion theorem and the upper bounds for the Fekete–Szegő functional 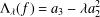${\rm\Lambda}_{{\it\lambda}}(f)=a_{3}-{\it\lambda}a_{2}^{2}$ for functions $f$ in the classes 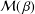${\mathcal{M}}(\,{\it\beta})$ and 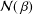${\mathcal{N}}(\,{\it\beta})$. Further, we shall solve the maximal area problem for functions of the type 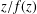$z/f(z)$ when 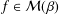$f\in {\mathcal{M}}(\,{\it\beta})$, which is Yamashita’s conjecture for the class 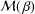${\mathcal{M}}(\,{\it\beta})$. We shall obtain the radius of convexity for the class 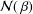${\mathcal{N}}(\,{\it\beta})$. We shall also determine the coefficient bounds for functions 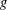$g$ in the classes 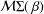${\mathcal{M}}{\rm\Sigma}(\,{\it\beta})$ and 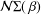${\mathcal{N}}{\rm\Sigma}(\,{\it\beta})$ and the inverse coefficient bounds for functions 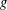$g$ in the class 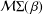${\mathcal{M}}{\rm\Sigma}(\,{\it\beta})$. All the results are sharp.

Keywords

univalentstarlikeconvex and hypergeometric functionscoefficient boundsradius of convexitymaximal area problem

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Secondary: 33C05: Classical hypergeometric functions, $_2F_1$
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 100 , Issue 1 , February 2016 , pp. 1 - 20
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Abdel-Gawad, H. R. and Thomas, D. K., ‘The Fekete–Szegő problem for strongly close-to-convex functions’, Proc. Amer. Math. Soc. 114(2) (1992), 345–349.Google Scholar
Bhowmik, B., Ponnusamy, S. and Wirths, K.-J., ‘On the Fekete–Szegő problem for concave univalent functions’, J. Math. Anal. Appl. 373 (2011), 432–438.CrossRefGoogle Scholar
Clunie, J. G., ‘On meromorphic schlicht functions’, J. Lond. Math. Soc. (2) 34 (1959), 215–216.CrossRefGoogle Scholar
Fekete, M. and Szegő, G., ‘Eine Bemerkung über ungerade schlichte Funktionen’, J. Lond. Math. Soc. (2) 8 (1933), 85–89.CrossRefGoogle Scholar
FitzGerald, C. H., ‘Quadratic inequalities and coefficient estimates for schlicht functions’, Arch. Ration. Mech. Anal. 46 (1972), 356–368.CrossRefGoogle Scholar
Goodman, A. W., Univalent Functions, I and II (Mariner, Tampa, FL, 1983).Google Scholar
Hallenbeck, D. J. and Ruscheweyh, St., ‘Subordination by convex functions’, Proc. Amer. Math. Soc. 52 (1975), 191–195.CrossRefGoogle Scholar
Jabotinsky, E., ‘Representation of functions by matrices: application to Faber polynomials’, Proc. Amer. Math. Soc. 4 (1953), 546–553.CrossRefGoogle Scholar
Jovanović, I. and Obradović, M., ‘A note on certain classes of univalent functions’, Filomat 9(1) (1995), 69–72.Google Scholar
Kapoor, G. P. and Mishra, A. K., ‘Coefficient estimates for inverses of starlike functions of positive order’, J. Math. Anal. Appl. 329 (2007), 922–934.CrossRefGoogle Scholar
Kirwan, W. E. and Schober, G., ‘Inverse coefficients for functions of bounded boundary rotations’, J. Anal. Math. 36 (1979), 167–178.CrossRefGoogle Scholar
Koepf, W., ‘On the Fekete–Szegő problem for close-to-convex functions’, Proc. Amer. Math. Soc. 101 (1987), 89–95.Google Scholar
Koepf, W., ‘On the Fekete–Szegő problem for close-to-convex functions II’, Arch. Math. 49 (1987), 420–433.CrossRefGoogle Scholar
Krzyż, J. G., Libera, R. J. and Złotkiewicz, E., ‘Coefficients of inverse of regular starlike functions’, Ann. Univ. Marie Curie-Sklodowska Sect. A 33(10) (1979), 103–109.Google Scholar
Libera, R. J. and Złotkiewicz, E. J., ‘Early coefficients of the inverse of a regular convex function’, Proc. Amer. Math. Soc. 85(2) (1982), 225–230.CrossRefGoogle Scholar
Libera, R. J. and Złotkiewicz, E. J., ‘Coefficient bounds for the inverse of a function with derivative in O-II’, Proc. Amer. Math. Soc. 92(1) (1984), 58–60.Google Scholar
Libera, R. J. and Złotkiewicz, E. J., ‘The coefficients of the inverse of an odd convex function’, Rocky Mountain J. Math. 15(3) (1985), 677–683.Google Scholar
Libera, R. J. and Złotkiewicz, E. J., ‘Löwner’s inverse coefficients theorem for starlike functions’, Amer. Math. Monthly 99(1) (1992), 49–50.Google Scholar
London, R. R., ‘Fekete–Szegő inequalities for close-to convex functions’, Proc. Amer. Math. Soc. 117 (1993), 947–950.Google Scholar
Löwner, K., ‘Untersuchungen über schlichte konforme Abbildungen des Einheitskreises I’, Math. Ann. 89 (1923), 103–121.CrossRefGoogle Scholar
Ma, W. and Minda, D., ‘A unified treatment of some special classes of univalent functions’, in: Proc. Conf. on Complex Analysis, Tianjin, China, 1992, Proceeding and Lecture Notes in Analysis, 1 (International Press, 1994), 157–169.Google Scholar
Miller, S. S. and Mocanu, P. T., Differential Subordinations: Theory and Applications, Monographs and Textbooks in Pure and Applied Mathematics, 225 (Marcel Dekker, New York, 2000).CrossRefGoogle Scholar
Nishiwaki, J. and Owa, S., ‘Coefficient inequalities for analytic functions’, Int. J. Math. Math. Sci. 29(5) (2002), 285–290.CrossRefGoogle Scholar
Obradović, M., Ponnusamy, S. and Wirths, K.-J., ‘Characteristics of the coefficients and partial sums of some univalent functions (Russian summary)’, Sibirsk. Mat. Zh. 54(4) (2013), 852–870; English translation in Sib. Math. J. 54(4) (2013), 679–696.Google Scholar
Obradović, M., Ponnusamy, S. and Wirths, K.-J., ‘A proof of Yamashita’s conjecture on area integral’, Comput. Methods Funct. Theory 13 (2013), 479–492.CrossRefGoogle Scholar
Obradović, M., Ponnusamy, S. and Wirths, K.-J., ‘Integral means and Dirichlet integral for analytic functions’, Math. Nachr. 288 (2015), 334–342.CrossRefGoogle Scholar
Owa, S. and Nishiwaki, J., ‘Coefficient estimates for certain classes of analytic functions’, J. Inequal. Pure Appl. Math. 3 (2002), 1–5.Google Scholar
Owa, S. and Srivastava, H. M., ‘Some generalized convolution properties associated with certain subclasses of analytic functions’, J. Inequal. Pure Appl. Math. 3 (2002), 1–13.Google Scholar
Ozaki, S., ‘On the theory of multivalent functions II’, Sci. Rep. Tokyo Bunrika Daigaku Sect. A 4 (1941), 45–87.Google Scholar
Pfluger, A., ‘The Fekete–Szegő inequality by a variational method’, Ann. Acad. Sci. Fenn. Math. Ser. AI 10 (1985), 447–454.Google Scholar
Pfluger, A., ‘The Fekete–Szegő inequality for complex parameters’, Complex Var. Theory Appl. 7 (1986), 149–160.Google Scholar
Pommerenke, Ch., Univalent Functions (Vandenhoeck and Ruprecht, Göttingen, 1975).Google Scholar
Ponnusamy, S. and Rajasekaran, S., ‘New sufficient conditions for starlike and univalent functions’, Soochow J. Math. 21(2) (1995), 193–201.Google Scholar
Ponnusamy, S. and Wirths, K.-J., ‘On the problem of Gromova and Vasil’ev on integral means, and Yamashita’s conjecture for spirallike functions’, Ann. Acad. Sci. Fenn. Math. Ser. AI 39 (2014), 721–731.CrossRefGoogle Scholar
Robertson, M. S., ‘Quasi-subordination and coefficient conjectures’, Bull. Amer. Math. Soc. 76 (1970), 1–9.CrossRefGoogle Scholar
Schaeffer, A. C. and Spencer, D. C., ‘The coefficients of schlicht functions. II’, Duke Math. J. 12 (1945), 107–125.CrossRefGoogle Scholar
Srivastava, H. M., Mishra, A. K. and Kund, S. N., ‘Coefficient estimates for the inverses of starlike functions represented by symmetric gap series (English summary)’, Panamer. Math. J. 21(4) (2011), 105–123.Google Scholar
Uralegaddi, B. A., Ganigi, M. D. and Sarangi, S. M., ‘Univalent functions with positive coefficients’, Tamkang J. Math. 25(3) (1994), 225–230.CrossRefGoogle Scholar
Yamashita, S., ‘Area and length maxima for univalent functions’, Bull. Aust. Math. Soc. 41(2) (1990), 435–439.CrossRefGoogle Scholar