Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T15:17:10.730Z Has data issue: false hasContentIssue false
  • English
  • Français

COCHAIN SEQUENCES AND THE QUILLEN CATEGORY OF A COCLASS FAMILY

Part of: Representation theory of groups Connections with homological algebra and category theory

Published online by Cambridge University Press:  12 May 2016

BETTINA EICK  and
DAVID J. GREEN
BETTINA EICK
Affiliation:
Institut Computational Mathematics, TU Braunschweig, 38106 Braunschweig, Germany email [email protected]
DAVID J. GREEN*
Affiliation:
Institut für Mathematik, Friedrich-Schiller-Universität Jena, 07737 Jena, Germany email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce the concept of infinite cochain sequences and initiate a theory of homological algebra for them. We show how these sequences simplify and improve the construction of infinite coclass families (as introduced by Eick and Leedham-Green) and also how they can be applied to prove that almost all groups in such a family have equivalent Quillen categories. We also include some examples of infinite families of 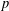$p$-groups from different coclass families that have equivalent Quillen categories.

Keywords

p-groupscoclassQuillen categoryextension class

MSC classification

Primary: 20D15: Nilpotent groups, $p$-groups
Secondary: 20J06: Cohomology of groups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 2 , April 2017 , pp. 185 - 204
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

Green received travel assistance from DFG grant GR 1585/6-1.

References

Adem, A. and Karagueuzian, D., ‘Essential cohomology of finite groups’, Comment. Math. Helv. 72(1) (1997), 101–109.CrossRefGoogle Scholar
Atiyah, M. F. and Macdonald, I. G., Introduction to Commutative Algebra (Addison-Wesley, Reading, MA, 1969).Google Scholar
Benson, D. J., Representations and Cohomology. I, Cambridge Studies in Advanced Mathematics, 30, 2nd edn (Cambridge University Press, Cambridge, 1998).Google Scholar
Cartan, H. and Eilenberg, S., Homological Algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
Couson, M., ‘On the character degrees and automorphism groups of finite $p$ -groups by coclass’, PhD Thesis, TU Braunschweig, 2013.CrossRefGoogle Scholar
Eick, B., ‘Automorphism groups of 2-groups’, J. Algebra 300(1) (2006), 91–101.CrossRefGoogle Scholar
Eick, B. and Feichtenschlager, D., ‘Computation of low-dimensional (co)homology groups for infinite sequences of p-groups with fixed coclass’, Internat. J. Algebra Comput. 21(4) (2011), 635–649.CrossRefGoogle Scholar
Eick, B. and Green, D. J., ‘The Quillen categories of p-groups and coclass theory’, Israel J. Math. 206(1) (2015), 183–212.CrossRefGoogle Scholar
Eick, B. and King, S., ‘The isomorphism problem for graded algebras and its application to mod-p cohomology rings of small p-groups’, J. Algebra 452 (2016), 487–501.CrossRefGoogle Scholar
Eick, B. and Leedham-Green, C., ‘On the classification of prime-power groups by coclass’, Bull. Lond. Math. Soc. 40 (2008), 274–288.CrossRefGoogle Scholar
Eick, B., Leedham-Green, C. R., Newman, M. F. and O’Brien, E. A., ‘On the classification of groups of prime-power order by coclass: the 3-groups of coclass 2’, Internat. J. Algebra Comput. 23(5) (2013), 1243–1288.CrossRefGoogle Scholar
Evens, L., The Cohomology of Groups (Oxford University Press, Oxford, 1991).CrossRefGoogle Scholar
Leedham-Green, C. R. and Mckay, S., The Structure of Groups of Prime Power Order, London Mathematical Society Monographs. New Series, 27 (Oxford Science Publications, Oxford University Press, Oxford, 2002).CrossRefGoogle Scholar
Leedham-Green, C. R. and Newman, M. F., ‘Space groups and groups of prime-power order. I’, Arch. Math. (Basel) 35(3) (1980), 193–202.CrossRefGoogle Scholar
Munkholm, H. J., ‘Mod 2 cohomology of D2 n and its extensions by Z 2 ’, in: Conference on Algebraic Topology (University of Illinois at Chicago Circle, Chicago, Illinois 1968) (University of Illinois, Chicago, Illinois, 1969), 234–252.Google Scholar
Quillen, D., ‘The spectrum of an equivariant cohomology ring. I, II’, Ann. of Math. (2) 94 (1971), 549–572; 573–602.CrossRefGoogle Scholar
Rusin, D. J., ‘The mod-2 cohomology of metacyclic 2-groups’, J. Pure Appl. Algebra 44(1–3) (1987), 315–327.CrossRefGoogle Scholar