Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T12:31:11.008Z Has data issue: false hasContentIssue false
  • English
  • Français

CLASSIFICATION OF UNIVALENT HARMONIC MAPPINGS ON THE UNIT DISK WITH HALF-INTEGER COEFFICIENTS

Part of: Geometric function theory

Published online by Cambridge University Press:  12 November 2014

SAMINATHAN PONNUSAMY  and
JINJING QIAO
SAMINATHAN PONNUSAMY*
Affiliation:
Indian Statistical Institute (ISI), Chennai Centre SETS (Society for Electronic Transactions and Security), MGR Knowledge City, CIT Campus, Taramani, Chennai 600 113, India email [email protected], [email protected]
JINJING QIAO
Affiliation:
Department of Mathematics, Hebei University, Baoding, Hebei 071002, PR China email [email protected]
*
✉[email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 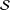${\mathcal{S}}$ denote the set of all univalent analytic functions 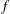$f$ of the form 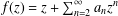$f(z)=z+\sum _{n=2}^{\infty }a_{n}z^{n}$ on the unit disk 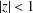$|z|<1$. In 1946, Friedman [‘Two theorems on Schlicht functions’, Duke Math. J.13 (1946), 171–177] found that the set 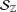${\mathcal{S}}_{\mathbb{Z}}$ of those functions in 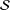${\mathcal{S}}$ which have integer coefficients consists of only nine functions. In a recent paper, Hiranuma and Sugawa [‘Univalent functions with half-integer coefficients’, Comput. Methods Funct. Theory13(1) (2013), 133–151] proved that the similar set obtained for functions with half-integer coefficients consists of only 21 functions; that is, 12 more functions in addition to these nine functions of Friedman from the set 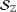${\mathcal{S}}_{\mathbb{Z}}$. In this paper, we determine the class of all normalized sense-preserving univalent harmonic mappings 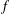$f$ on the unit disk with half-integer coefficients for the analytic and co-analytic parts of 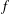$f$. It is surprising to see that there are only 27 functions out of which only six functions in this class are not conformal. This settles the recent conjecture of the authors. We also prove a general result, which leads to a new conjecture.

Keywords

typically real analytic mappingsharmonic mappingsunivalentstarlikeconvexclose-to-convextypically real harmonic mappingsconvex in real directionconvex in imaginary directionSchwarz lemmasubordinationhalf-integer coefficientsuniformly discrete set

MSC classification

Primary: 30C65: Quasiconformal mappings in $^n$, other generalizations
Secondary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.) 30C20: Conformal mappings of special domains
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 98 , Issue 2 , April 2015 , pp. 257 - 280
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Bshouty, D., Hengartner, W. and Hossian, O., ‘Harmonic typically real mappings’, Math. Proc. Cambridge Philos. Soc. 119(4) (1996), 673–680.Google Scholar
Clunie, J. G. and Sheil-Small, T., ‘Harmonic univalent functions’, Ann. Acad. Sci. Fenn. Ser. A I 9 (1984), 3–25.Google Scholar
Dorff, M., ‘Convolutions of planar harmonic convex mappings’, Complex Var. Theory Appl. 45 (2001), 263–271.Google Scholar
Dorff, M., ‘Anamorphosis, mapping problems, and harmonic univalent functions’, in: Explorations in Complex Analysis (Mathematical Association of America, Washington, DC, 2012), 197–269.Google Scholar
Dorff, M., Nowak, M. and Szapiel, W., ‘Typically real harmonic functions’, Rocky Mountain J. Math. 42(92) (2012), 567–581.CrossRefGoogle Scholar
Duren, P., Univalent Functions (Springer, New York–Berlin–Heidelberg–Tokyo, 1982).Google Scholar
Duren, P., Harmonic Mappings in the Plane (Cambridge University Press, New York, 2004).CrossRefGoogle Scholar
FitzGerald, C. H., ‘Quadratic inequalities and coefficient estimates for Schlicht functions’, Arch. Ration. Mech. Anal. 46 (1972), 356–368.CrossRefGoogle Scholar
Friedman, B., ‘Two theorems on Schlicht functions’, Duke Math. J. 13 (1946), 171–177.CrossRefGoogle Scholar
Goodman, A. W., Univalent Functions, Vols. 1–2 (Mariner, Tampa, FL, 1983).Google Scholar
Greiner, P., ‘Geometric properties of harmonic shears’, Comput. Methods Funct. Theory 4(1) (2004), 77–96.Google Scholar
Gronwall, T. H., ‘Some remarks on conformal representation’, Ann. of Math. (2) 16 (1914–1915), 72–76.Google Scholar
Hengartner, W. and Schober, G., ‘On Schlicht mappings to domains convex in one direction’, Comment. Math. Helv. 45 (1970), 303–314.CrossRefGoogle Scholar
Hiranuma, N. and Sugawa, T., ‘Univalent functions with half-integral coefficients’, Comput. Methods Funct. Theory 13(1) (2013), 133–151; see also arXiv:1208.2483.Google Scholar
Jenkins, J. A., ‘On univalent functions with integral coefficients’, Complex Var. Theory Appl. 9 (1987), 221–226.Google Scholar
Lecko, A., ‘On the class of functions convex in the negative direction of the imaginary axis’, J. Aust. Math. Soc. 73 (2002), 1–10.CrossRefGoogle Scholar
Lewy, H., ‘On the nonvanishing of the Jacobian in certain one-to-one mappings’, Bull. Amer. Math. Soc. 42 (1936), 689–692.Google Scholar
Linis, V., ‘Note on univalent functions’, Amer. Math. Monthly 62 (1955), 109–110.Google Scholar
Obradović, M. and Ponnusamy, S., ‘New criteria and distortion theorems for univalent functions’, Complex Var. Theory Appl. 44 (2001), 173–191.Google Scholar
Pommerenke, Ch., Univalent Functions (Vandenhoeck and Ruprecht, Göttingen, 1975).Google Scholar
Ponnusamy, S. and Qiao, J., ‘Univalent harmonic mappings with integer or half-integer coefficients’, Preprint, 2012, see arXiv:1207.3768.Google Scholar
Robertson, M. S., ‘Analytic functions starlike in one direction’, Amer. J. Math. 58 (1936), 465–472.CrossRefGoogle Scholar
Rogosinski, W., ‘Über positive harmonische Entwicklungen und typisch-reelle Potenzreihen’, Math. Z. 35(1) (1932), 93–121; (in German).Google Scholar
Rogosinski, W., ‘On the coefficients of subordinate functions’, Proc. Lond. Math. Soc. (3) 48 (1943), 48–82.Google Scholar
Royster, W. C., ‘Rational univalent functions’, Amer. Math. Monthly 63 (1956), 326–328.Google Scholar
Royster, W. C. and Ziegler, M., ‘Univalent functions convex in one direction’, Publ. Math. Debrecen 23 (1976), 339–345.Google Scholar
Shah, T.-S., ‘On the coefficients of Schlicht functions’, J. Chin. Math. Soc. (N.S.) 1 (1951), 98–107.Google Scholar
Suffridge, T. J., ‘Harmonic univalent polynomials’, Complex Var. Theory Appl. 35(2) (1998), 93–107.Google Scholar
Townes, S. B., ‘A theorem on Schlicht functions’, Proc. Amer. Math. Soc. 5 (1954), 585–588.Google Scholar