Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T22:32:32.673Z Has data issue: false hasContentIssue false
  • English
  • Français

A classification of the commutator subgroup of the group of a boundary link

Published online by Cambridge University Press:  09 April 2009

Bai Ching Chang
Bai Ching Chang
Affiliation:
University of Western Australia, Nedlands, West Australia, 6009
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In Neuwirth's book “Knot Groups” ([2]), the structure of the commutator subgroup of a knot is studied and characterized. Later Brown and Crowell refined Neuwith's result ([1], and we thus know that if G is the groups of a knot K, then [G, G] is either free of rank 2g, where g is the genus of K, or a nontrivial free product with amalgamation on a free group of rank 2g, and may be written in the form 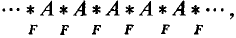, where F is free of rank 2g, and the amalgamations are all proper and identical.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 18 , Issue 2 , September 1974 , pp. 216 - 221
Copyright
Copyright © Australian Mathematical Society 1974

References

[1]Brown, E. M. and Crowell, R. H., ‘Deformation retract of 3-manifolds into their boundaries’, Ann. of Math. 82 (1965), 445–448.CrossRefGoogle Scholar
[2]Neuwirth, L. P., Knot Groups Annals of Mathematical Studies, No. 56 (Princeton University Press) (1965).CrossRefGoogle Scholar
[3]Papakyriakopoulos, C. D., ‘On solid tori’, Proc. London Math. Soc. (3) 1 (1957), 281–299.CrossRefGoogle Scholar
[4]Papakyriakopoulos, C. D., ‘On Dehn's lemma and the asphericity of knots’, Proc. Nat. Acad. Soc. U.S.A. 43 (1957), 169–172.CrossRefGoogle Scholar