Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-23T02:37:52.197Z Has data issue: false hasContentIssue false
  • English
  • Français

A class of multipliers

Published online by Cambridge University Press:  09 April 2009

R. E. Edwards
R. E. Edwards
Affiliation:
Department of MathematicsInstitute of Advanced Studies Australian National University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper G denotes an infinite compact connected Hausdorff Abelian group with character group X. Given a map of α X into itself, we are concerned with the set of a, ∈ G such that the function ϕa ∈ l∞ (X) defined by 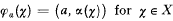is a multiplier of type (þ, þ), where it can be assumed without loss of generality that 1 ≤ þ < ∞.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 3 , August 1968 , pp. 584 - 590
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Rudin, W., Fourier analysis on groups (Interscience Publishers 1962).Google Scholar
[2]Edwards, R. E., ‘Translates of L∞ functions and of bounded measures’, J. Austr. Math. Soc. 4 (1964), 403–409.CrossRefGoogle Scholar
[3]Zygmund, A., Trigonometric series, Vol. 1 (Cambridge University Press 1959).Google Scholar
[4]Helgason, S., ‘Multipliers of Banach algebras’, Ann. of Math. 64 (1956), 240–254.CrossRefGoogle Scholar
[5]Weyl, H., ‘Über die Gleichverteilung von Zahlen mod. Eins’, Math. Ann. 77 (1916), 313–352.CrossRefGoogle Scholar