Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T02:30:46.205Z Has data issue: false hasContentIssue false
  • English
  • Français

The class L(log L)α and some lacunary sets

Part of: Harmonic analysis in one variable

Published online by Cambridge University Press:  09 April 2009

Sanjiv Kumar Gupta ,
Shobha Madan  and
U. B. Tewari
Sanjiv Kumar Gupta
Affiliation:
Department of MathematicsIndian Institute of Technology KanpurKanpur, 208016, India
Shobha Madan
Affiliation:
Department of MathematicsIndian Institute of Technology KanpurKanpur, 208016, India
U. B. Tewari
Affiliation:
Department of MathematicsIndian Institute of Technology KanpurKanpur, 208016, India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A well-known result of Zygmund states that if f ∈ L (log+L) ½ on the circle group T and E is a Hadamard set of integers, then 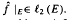. In this paper we investigate similar results for the classes 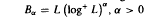on an arbitrary infinite compact abelian group G and Sidon subsets E of the dual Γ. These results are obtained as special cases of more general results concerning a new class of lacunary sets Sαβ, 0 < α ≤ β, where a subset E of Γ is an Sα β set if 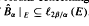. We also prove partial results on the distinctness of the Sαβ sets in the index β.

Keywords

lacunary sets.

MSC classification

Secondary: 42A55: Lacunary series of trigonometric and other functions; Riesz products 42A05: Trigonometric polynomials, inequalities, extremal problems
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 58 , Issue 3 , June 1995 , pp. 387 - 403
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]Hewitt, E. and Ross, K. A., Abstract harmonic analysis I, Grundlehren Math. Wiss. 115 (Springer Berlin, 1963).Google Scholar
[2]Hewitt, E. and Ross, K. A., Abstract harmonic analysis II, Grundlehren Math. Wiss. 152 (Springer, Berlin, 1970).Google Scholar
[3]Krasnosel'skii, M. A. and Rutickii, Ya. B., Convex functions and Orlicz spaces (Gronigen, 1961), (Translated from the Russian).Google Scholar
[4]Lopez, J. M. and Ross, K. A., Sidon sets, Lectures Notes in Pure and Appl. Math. 13 (Marcel Dekker, New York, 1970).Google Scholar
[5]Pisiér, G., ‘Ensembles de sidon processus Gaussiens’, C. R. Acad. Sci. Paris Sér. l Math. 286A (1978), 671–674.Google Scholar
[6]Zygmund, A., Trigonometric series II (Cambridge Univ. Press, London, 1979).Google Scholar