Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1994.
Graph Coloring Problems.
p.
150.
Kupavskii, A. B.
2009.
Lifting of a bound for the chromatic number of ℝ n to higher dimensions.
Doklady Mathematics,
Vol. 80,
Issue. 3,
p.
833.
Raigorodskii, A. M.
2010.
On the chromatic numbers of spheres in Euclidean spaces.
Doklady Mathematics,
Vol. 81,
Issue. 3,
p.
379.
Soifer, Alexander
2011.
Ramsey Theory.
p.
121.
Kupavskii, Andrei B
2011.
On the colouring of spheres embedded in $ \mathbb R^n$.
Sbornik: Mathematics,
Vol. 202,
Issue. 6,
p.
859.
Купавский, Андрей Борисович
and
Kupavskii, Andrey Borisovich
2011.
О раскрасках сфер, вложенных в $\mathbb R^n$.
Математический сборник,
Vol. 202,
Issue. 6,
p.
83.
Raigorodskii, A. M.
2012.
On the chromatic numbers of spheres in ℝ n.
Combinatorica,
Vol. 32,
Issue. 1,
p.
111.
Raigorodskii, Andrei M.
2013.
Thirty Essays on Geometric Graph Theory.
p.
429.
Holmsen, Andreas F.
and
Lee, Seunghun
2016.
ORTHOGONAL COLORINGS OF THE SPHERE.
Mathematika,
Vol. 62,
Issue. 2,
p.
492.
Yegnanarayanan, V.
2017.
Prime distance graphs and applications.
p.
1564.
Kostina, O. A.
2019.
On Lower Bounds for the Chromatic Number of Spheres.
Mathematical Notes,
Vol. 105,
Issue. 1-2,
p.
16.
Kostina, Olga Andreevna
2019.
О нижних оценках хроматического числа сферы.
Математические заметки,
Vol. 105,
Issue. 1,
p.
18.
Voronov, V.A.
Neopryatnaya, A.M.
and
Dergachev, E.A.
2022.
Constructing 5-chromatic unit distance graphs embedded in the Euclidean plane and two-dimensional spheres.
Discrete Mathematics,
Vol. 345,
Issue. 12,
p.
113106.
Soifer, Alexander
2024.
The New Mathematical Coloring Book.
p.
23.
Cherkashin, Danila
and
Voronov, Vsevolod
2024.
On the Chromatic Number of 2-Dimensional Spheres.
Discrete & Computational Geometry,
Vol. 71,
Issue. 2,
p.
467.
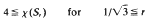 and that this bound is best possible since
and that this bound is best possible since 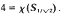 .
.