Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T20:58:21.190Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERIZING SOME COMPLETELY REGULAR SEMIGROUPS BY THEIR SUBSEMIGROUPS

Part of: Semigroups

Published online by Cambridge University Press:  07 June 2013

MARIO PETRICH
MARIO PETRICH*
Affiliation:
21420 Bol, Brač, Croatia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider several familiar varieties of completely regular semigroups such as groups and completely simple semigroups. For each of them, we characterize their members in terms of absence of certain kinds of subsemigroups, as well as absence of certain divisors, and in terms of a homomorphism of a concrete semigroup into the semigroup itself. For each of these varieties 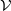$ \mathcal{V} $ we determine minimal non-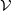$ \mathcal{V} $ varieties, provide a basis for their identities, determine their join and give a basis for its identities. Most of this is complete; one of the items missing is a basis for identities for minimal nonlocal orthogroups. Three tables and a figure illustrate the results obtained.

Keywords

completely regular semigroupsubsemigroupdivisorhomomorphismvarietyminimal non- 𝓥 varietyjoinorthogroupcryptogroup

MSC classification

Secondary: 20M10: General structure theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 3 , June 2013 , pp. 397 - 416
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Jones, P. R., ‘Mal’cev products of varieties of completely regular semigroups’, J. Aust. Math. Soc. Ser. A 42 (1987), 227–246.CrossRefGoogle Scholar
Petrich, M., ‘Characterizations of certain completely regular varieties’, Semigroup Forum 66 (2003), 381–400.CrossRefGoogle Scholar
Petrich, M., ‘Characterizing cryptogroups with a finite number of $ \mathcal{H} $-classes in each $ \mathcal{D} $-class by their subsemigroups’, Ann. Mat. Pura Appl. (4) 187 (2008), 119–136.CrossRefGoogle Scholar
Petrich, M., ‘Completely regular monoids with two generators’, J.  Aust. Math. Soc. 90 (2011), 271–287.CrossRefGoogle Scholar
Petrich, M. and Reilly, N. R., ‘Operators related to $E$-disjunctive and fundamental completely regular semigroups’, J. Algebra 134 (1990), 1–27.CrossRefGoogle Scholar
Petrich, M. and Reilly, N. R., Completely Regular Semigroups (Wiley, New York, 1999).Google Scholar
Reilly, N. R., ‘Varieties of completely regular semigroups’, J. Aust. Math. Soc. Ser. A 38 (1985), 372–393.CrossRefGoogle Scholar
Trotter, P. G., ‘Subdirect decompositions of the lattice of varieties of completely regular semigroups’, Bull. Aust. Math. Soc. 39 (1989), 343–351.CrossRefGoogle Scholar