In this paper, using pseudo path algebras, we generalize Gabriel's Theorem on elementary algebras to left Artinian algebras over a field k when the quotient algebra can be lifted by a radical. Our particular interest is when the dimension of the quotient algebra determined by the nth Hochschild cohomology is less than 2 (for example, when k is finite or char k = 0). Using generalized path algebras, a generalization of Gabriel's Theorem is given for finite dimensional algebras with 2-nilpotent radicals which is splitting over its radical. As a tool, the so-called pseudo path algebra is introduced as a new generalization of path algebras, whose quotient by ken is a generalized path algebra (see Fact 2.6).

The main result is that

(i) for a left Artinian k–algebra A and r = r(A) the radical of A. if the quotient algebra A/r can be lifted then A ≅ PSEk (Δ, 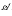, ρ) with Js ⊂ (ρ) ⊂ J for some s (Theorem 3.2);

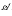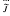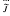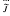(ii) If A is a finite dimensional k–algebra with 2-nilpotent radical and the quotient by radical can be lifted, then A ≅ k(Δ, , ρ) with 2 ⊂ (ρ) ⊂ 2 + ∩ ker 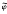(Theorem 4.2),

where Δ is the quiver of A and ρ is a set of relations.

For all the cases we discuss in this paper, we prove the uniqueness of such quivers Δ and the generalized path algebras/pseudo path algebras satisfying the isomorphisms when the ideals generated by the relations are admissible (see Theorem 3.5 and 4.4).