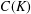Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-20T04:56:44.526Z Has data issue: false hasContentIssue false
  • English
  • Français

CHAINS OF FUNCTIONS IN $C(K)$-SPACES

Part of: Special properties Complex dynamical systems Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  02 September 2015

TOMASZ KANIA  and
RICHARD J. SMITH
TOMASZ KANIA*
Affiliation:
Department of Mathematics and Statistics, Fylde College, Lancaster University, Lancaster LA1 4YF, UK Institute of Mathematics, Polish Academy of Sciences, Śniadeckich 8, 00-056 Warszawa, Poland email [email protected]
RICHARD J. SMITH
Affiliation:
School of Mathematical Sciences, University College Dublin, Belfield, Dublin 4, Ireland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Bishop property (♗), introduced recently by K. P. Hart, T. Kochanek and the first-named author, was motivated by Pełczyński’s classical work on weakly compact operators on 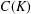$C(K)$-spaces. This property asserts that certain chains of functions in said spaces, with respect to a particular partial ordering, must be countable. There are two versions of (♗): one applies to linear operators on 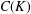$C(K)$-spaces and the other to the compact Hausdorff spaces themselves. We answer two questions that arose after (♗) was first introduced. We show that if 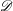$\mathscr{D}$ is a class of compact spaces that is preserved when taking closed subspaces and Hausdorff quotients, and which contains no nonmetrizable linearly ordered space, then every member of 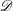$\mathscr{D}$ has (♗). Examples of such classes include all 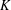$K$ for which 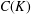$C(K)$ is Lindelöf in the topology of pointwise convergence (for instance, all Corson compact spaces) and the class of Gruenhage compact spaces. We also show that the set of operators on a 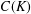$C(K)$-space satisfying (♗) does not form a right ideal in 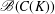$\mathscr{B}(C(K))$. Some results regarding local connectedness are also presented.

Keywords

compact spacelinear orderinguncountable chain

MSC classification

Secondary: 54F05: Linearly ordered topological spaces, generalized ordered spaces, and partially ordered spaces 37F20: Combinatorics and topology 46B26: Nonseparable Banach spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 3 , December 2015 , pp. 350 - 363
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Alster, K. and Pol, R., ‘On function spaces of compact subspaces of Σ-products of the real-line’, Fund. Math. 107 (1980), 135–143.CrossRefGoogle Scholar
Bennett, H. and Lutzer, D., ‘The Gruenhage property, property *, fragmentability, and 𝜎-isolated networks in generalized ordered spaces’, Fund. Math. 223 (2013), 273–294.CrossRefGoogle Scholar
Dow, A. and Simon, P., ‘Spaces of continuous functions over a Ψ-space’, Topology Appl. 153 (2006), 2260–2271.CrossRefGoogle Scholar
Gruenhage, G., ‘A note on Gul’ko compact spaces’, Proc. Amer. Math. Soc. 100 (1987), 371–376.Google Scholar
Gul’ko, S. P., ‘On the properties of some function spaces’, Sov. Math. Dokl. 19 (1978), 1420–1424.Google Scholar
Hart, K. P., Kania, T. and Kochanek, T., ‘A chain condition for operators from C (K)-spaces’, Q. J. Math. 65 (2014), 703–715.CrossRefGoogle Scholar
Haydon, R., ‘Locally uniformly convex norms in Banach spaces and their duals’, J. Funct. Anal. 254 (2008), 2023–2039.CrossRefGoogle Scholar
Jech, T., Set Theory, The Third Millennium Edition, Revised and Expanded, Springer Monographs in Mathematics (Springer, Berlin, 2006).Google Scholar
Leung, C.-W., Ng, C.-K. and Wong, N.-C., ‘Geometric pre-ordering on C*-algebras’, J. Operator Theory 63 (2010), 115–128.Google Scholar
Nakhmanson, L. B., ‘On the tightness of L p(X) of a linearly ordered compact space X’, in: Investigations in the Theory of Approximations, Vol. 123 (Ural’skogo Gosudarstvennogo Universiteta, Sverdlovsk, 1988), 71–74 (in Russian).Google Scholar
Orihuela, J., Smith, R. J. and Troyanski, S., ‘Strictly convex norms and topology’, Proc. Lond. Math. Soc. 104 (2012), 197–222.CrossRefGoogle Scholar
Rosenstein, J. G., Linear Orderings, Pure and Applied Mathematics, 98 (Academic Press, New York, 1981).Google Scholar
Smith, R. J., ‘Gruenhage compacta and strictly convex dual norms’, J. Math. Anal. Appl. 350 (2009), 745–757.CrossRefGoogle Scholar
Smith, R. J., ‘Strictly convex norms, G 𝛿 -diagonals and non-Gruenhage spaces’, Proc. Amer. Math. Soc. 140 (2012), 3117–3125.CrossRefGoogle Scholar
Todorčević, S., ‘Stationary sets, trees and continuums’, Publ. Inst. Math. (Beograd) 29 (1981), 109–122.Google Scholar